Temas
Primeiro, vamos relembrar que as variações de  elementos tomados de
elementos tomados de  em
em  são dadas pela fórmula
são dadas pela fórmula
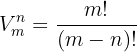
em que 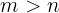 .
.
Da mesma forma, as variações com repetição de  elementos tomados
elementos tomados  a
a  são dadas por:
são dadas por:
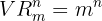
onde 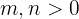 , mas sem restrições entre eles.
, mas sem restrições entre eles.
Agora que relembramos essas definições, vamos aos exercícios.

Exercícios com números
Quantos números de três algarismos (todos diferentes) podem ser formados com os números  ?
?
Fica claro que se trata de variações, pois:
1. Não usamos todos os elementos. Apenas três dos cinco números serão escolhidos.
2. A ordem importa. Não é o mesmo formar  que
que  .
.
3. Os elementos não se repetem. Uma vez que escolhemos um número, ele não pode ser reutilizado, já que todos os algarismos devem ser diferentes.
Portanto, temos uma variação de  elementos tomados de
elementos tomados de  em
em  , ou seja,
, ou seja,  e
e  , e a quantidade de números que podemos formar é
, e a quantidade de números que podemos formar é
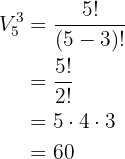
Quantos números de três algarismos (permitindo a repetição de algarismos) podem ser formados com os números  ?
?
Fica claro que se trata de variações, pois:
1. Não usamos todos os elementos. Apenas três dos cinco números serão escolhidos.
2. A ordem importa. Não é o mesmo formar  que
que  .
.
3. Os elementos podem se repetir. O próprio enunciado diz que é permitido repetir algarismos, ou seja, são válidos números como 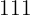 ,
, 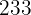 ,
, 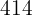 , etc.
, etc.
Portanto, temos uma variação com repetição de  elementos tomados de
elementos tomados de  em
em  , ou seja,
, ou seja,  e
e  , e a quantidade de números que podemos formar é:
, e a quantidade de números que podemos formar é:
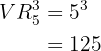
Quantos números de três algarismos (todos diferentes) podem ser formados com os números  ?
?
Perceba que esse caso é um pouco mais complexo, já que o primeiro algarismo precisa ser, obrigatoriamente, diferente de zero.
Por isso, temos  possibilidades: os números
possibilidades: os números 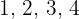 e
e  . Isso quer dizer que temos uma variação de
. Isso quer dizer que temos uma variação de  elementos tomados de
elementos tomados de  em
em  :
:
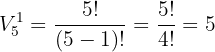
Agora, depois de escolher o primeiro número, restam  números livres mais o
números livres mais o  , já que este pode aparecer como segundo ou terceiro algarismo. Portanto, voltamos a ter
, já que este pode aparecer como segundo ou terceiro algarismo. Portanto, voltamos a ter  opções. Nesse caso, tanto o segundo quanto o terceiro algarismo serão escolhidos entre cinco números, com a única restrição de que não podem se repetir. Isso nos leva a uma variação de
opções. Nesse caso, tanto o segundo quanto o terceiro algarismo serão escolhidos entre cinco números, com a única restrição de que não podem se repetir. Isso nos leva a uma variação de  elementos tomados de
elementos tomados de  em
em  , pois:
, pois:
1. Não usamos todos os elementos. Apenas dois dos cinco serão escolhidos.
2. A ordem importa. Não é o mesmo formar  que
que  .
.
3. Os elementos não se repetem. O próprio exercício diz que todos os algarismos devem ser diferentes.
Assim, temos  e
e 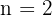 para essas variações.
para essas variações.
A resposta será a multiplicação das variações para o primeiro algarismo pelas variações do segundo e terceiro algarismos:
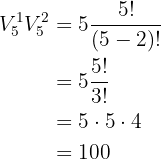
Quantos números de três algarismos (permitindo repetições) podem ser formados com os números  ?
?
Assim como no caso anterior, esse também é um pouco mais complexo, já que o primeiro algarismo precisa ser, obrigatoriamente, diferente de zero. Por isso, temos  possibilidades: os números
possibilidades: os números 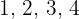 e
e  . Isso corresponde a uma variação de
. Isso corresponde a uma variação de  elementos tomados de
elementos tomados de  em
em  :
:
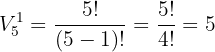
Agora, depois de escolher o primeiro número, a segunda e a terceira posição podem ser preenchidas por qualquer um dos seis números disponíveis, já que não há restrição quanto à repetição. Assim, temos uma variação com repetição de  elementos tomados de
elementos tomados de  em
em  , pois:
, pois:
1. Não usamos todos os elementos. Apenas dois dos seis serão escolhidos.
2. A ordem importa. Não é o mesmo formar  que
que  .
.
3. Os elementos podem se repetir. Isso é explicitado no próprio enunciado.
Sabemos, então, que nessa variação com repetição temos 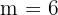 e
e 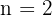 .
.
Assim, a resposta será dada pela multiplicação da quantidade de variações para o primeiro algarismo pela quantidade de variações com repetição pelas variações do segundo e terceiro algarismos:
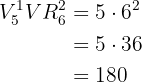
Quantos números de cinco algarismos podem ser formados com os números 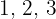 ?
?
Primeiramente, repare que o exercício pede que formemos um número com cinco algarismos, sendo que cada algarismo pode assumir apenas três valores. Como estamos tentando formar uma sequência maior do que a quantidade de elementos disponíveis, temos que assumir repetição, pois, caso não fosse permitido repetir os números, o máximo de algarismos que conseguiríamos seria  .
.
Além disso, as seguintes condições são atendidas:
1. Todos os elementos podem ser utilizados;
2. A ordem importa — por exemplo,  é diferente de
é diferente de  ;
;
3. A repetição é permitida — o próprio enunciado nos leva a deduzir isso.
Logo, trata-se de uma variação com repetição de  elementos tomados de
elementos tomados de  em
em  , ou seja,
, ou seja, 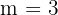 e
e  .
.
Assim, a quantidade de números que podem ser formados é dada por:
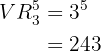
Exercícios aplicados a esportes
Quantos bilhetes de aposta com uma única coluna precisam ser preenchidos para garantir o acerto dos  resultados?
resultados?
Primeiro, vamos entender o que é esse tipo de aposta. Em um cartão de apostas, há uma coluna com  jogos, e cada jogo tem
jogos, e cada jogo tem  resultados possíveis: vitória do time da casa, vitória do time visitante ou empate. Perceba que estamos lidando com variações com repetição, onde
resultados possíveis: vitória do time da casa, vitória do time visitante ou empate. Perceba que estamos lidando com variações com repetição, onde 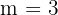 ,
, 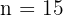 e
e 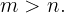 . Além disso, observamos que:
. Além disso, observamos que:
1. Todos os elementos entram em consideração.
2. A ordem importa. Não é o mesmo dizer que o time da casa venceu no primeiro jogo e o visitante no segundo, do que o contrário.
3. Os elementos se repetem. É perfeitamente possível que dois jogos diferentes terminem empatados ou com vitórias dos mesmos times.
Assim, temos que a quantidade de cartões de apostas necessários para garantir o acerto de todos os resultados é:
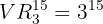
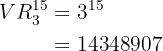
Quantos jogos tem um torneio com quatro times?
Observe que valem as seguintes condições:
1. Todos os elementos são usados (os 4 times participam).
2. A ordem importa: O time da esquerda é considerado o mandante e o da direita, o visitante. Portanto, A vs B é diferente de B vs A.
3. Não há repetição: Não é possível um jogo do tipo A vs A.
Assim, temos um caso de arranjos simples, onde  e
e 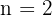 .
.
Portanto, o número de jogos possíveis é:
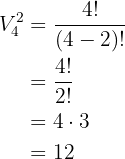
De quantas formas diferentes podemos preencher os cargos de presidente, vice-presidente e tesoureiro de um clube de futebol, sabendo que há 12 candidatos possíveis?
Observe que valem as seguintes condições:
1. Todos os elementos são considerados (os 12 candidatos estão disponíveis para os cargos)
2. A ordem importa: Não é a mesma coisa João como presidente e Leila como vice-presidente, vs Leila como presidente e João como vice-presidente
3. Não há repetição: Uma mesma pessoa não pode ocupar mais de um cargo
Portanto, temos um caso de arranjos simples onde: 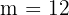 e
e  .
.
O número de formas diferentes de preencher os cargos é dado por:
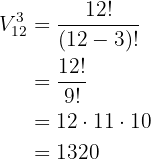
Problemas de variações com temas diversos
Dez candidatos inscreveram seus livros em um concurso literário. O pódio é formado pelo vencedor, o finalista e um menção honrosa. De quantos maneiras diferentes pode ser formado o pódio de um concurso literário com 10 candidatos?
Observe que temos as seguintes condições:
1. Todos os elementos são considerados (os 10 candidatos concorrem)
2. A ordem importa: Não é a mesma coisa Fernanda ser a vencedora e Pedro o finalista vs Pedro ser o vencedor e Fernanda a finalista
3. Não há repetição: Um mesmo candidato não pode ocupar mais de uma posição no pódio
Portanto, temos um caso de arranjos simples onde: 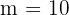 e
e  . O número de pódios distintos possíveis é dado por:
. O número de pódios distintos possíveis é dado por:
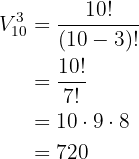
Com o (ponto, traço) do sistema Morse, quantos sinais distintos podem ser enviados, utilizando no máximo quatro pulsações?
Primeiro, temos que perceber que ao dizer que são no máximo quatro pulsações, significa que devemos considerar os casos com apenas uma pulsação, com duas, com três e com quatro. Portanto, será necessário considerar cada um desses casos separadamente e, ao final, somar todos eles.
Observe que, quando há apenas uma pulsação, temos apenas duas opções possíveis: pode ser um ponto ou pode ser um traço.
Agora, de forma geral, para qualquer número de pulsações maior que  , temos que satisfazer as seguintes condições:
, temos que satisfazer as seguintes condições:
1. Todos os elementos estão incluídos.
2. A ordem importa.
3. Os elementos podem se repetir. Podemos ter, por exemplo, dois pontos ou dois traços consecutivos.
Assim, para duas pulsações, a quantidade de sinais distintos que podemos formar é:
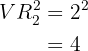
Para três pulsações, a quantidade de sinais distintos que podemos formar é:
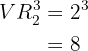
Para quatro pulsações, a quantidade de sinais distintos que podemos formar é:
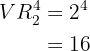
Dessa forma, no final, vamos ter que, para máximo de quatro pulsações a quantidade sinais distintos que podemos formar é:
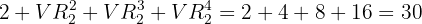
Determine a quantidade de números palíndromos de oito algarismos.
Um número palíndromo é aquele que se lê da mesma forma da esquerda para a direita e da direita para a esquerda. Portanto, um número palíndromo de oito algarismos tem a seguinte forma:
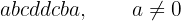
em que  e
e  são seus algarismos.
são seus algarismos.
Note que, na verdade, o problema é equivalente a determinar quantos números diferentes de  algarismos podemos formar com os dígitos de
algarismos podemos formar com os dígitos de  a
a  (dez dígitos).
(dez dígitos).
Aqui, o dígito  deve ser estritamente diferente de
deve ser estritamente diferente de  , enquanto
, enquanto 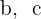 e
e  podem assumir qualquer valor, incluindo o
podem assumir qualquer valor, incluindo o  , e com repetição — ou seja,
, e com repetição — ou seja,  pode ser igual a
pode ser igual a  .
.
Mas como resolvemos isso? Não é complicado; é igual ao exercício  . Primeiro, consideramos o caso de
. Primeiro, consideramos o caso de  . Note que para
. Note que para  temos
temos  opções distintas, já que o
opções distintas, já que o  não é permitido.
não é permitido.
Agora, para  ,
,  e
e  , temos
, temos  possibilidades para cada um. Assim, temos uma situação de variações com repetição, em que
possibilidades para cada um. Assim, temos uma situação de variações com repetição, em que 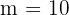 e
e  , e onde se verifica que:
, e onde se verifica que:
1. Todos os elementos entram.
2. A ordem importa.
3. Os elementos podem se repetir.
Portanto, a quantidade de formas diferentes de escolher  ,
,  e
e  é dada por:
é dada por:
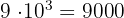
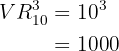
Para obter o número de palíndromos de  algarismos, basta multiplicar a quantidade de possibilidades para o primeiro algarismo pela quantidade de casos para o segundo, terceiro e quarto algarismos. Ou seja:
algarismos, basta multiplicar a quantidade de possibilidades para o primeiro algarismo pela quantidade de casos para o segundo, terceiro e quarto algarismos. Ou seja:
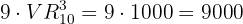
Equações de combinatória
Resolva: 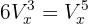
Para resolver, basta aplicarmos diretamente a fórmula das variações:
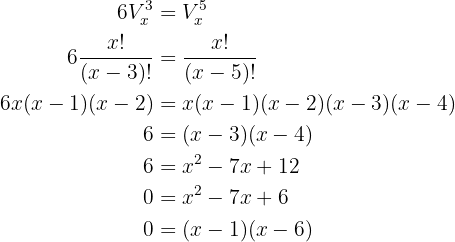
De onde se conclui que as soluções são  e
e  .
.
No entanto, lembre-se que 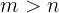 , ou seja,
, ou seja,  deve ser maior que
deve ser maior que  e maior que
e maior que  .
.
Assim, a única solução possível é  .
.
Resolva: 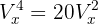
Para resolver, basta aplicarmos diretamente a fórmula das variações:
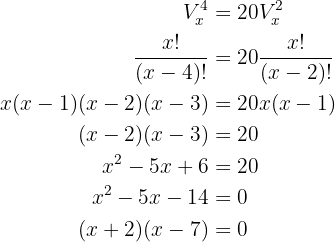
De onde se conclui que as soluções são  e
e  .
.
No entanto, lembre-se que 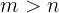 , ou seja,
, ou seja,  deve ser maior que
deve ser maior que  e maior que
e maior que  .
.
Desse modo, a única solução possível é  (além disso,
(além disso,  não pode ser negativo).
não pode ser negativo).
Resolva: 
Para resolver, basta aplicarmos diretamente a fórmula das variações:
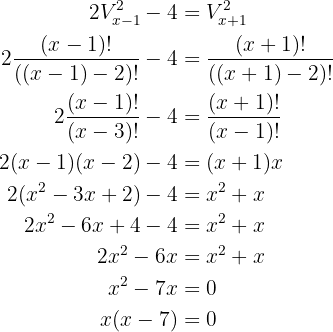
De onde se conclui que as soluções são  e
e  , no entanto, lembre-se que
, no entanto, lembre-se que 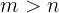 , então
, então  deve ser maior que
deve ser maior que  , assim, a única solução possível é
, assim, a única solução possível é  (além disso,
(além disso,  não pode ser
não pode ser  ).
).
Resolva: 
Para resolver, basta aplicarmos diretamente a fórmula das variações:
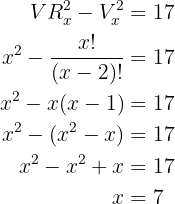
Neste caso, a única solução possível é: 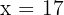 .
.
Resumir com IA:












