Temas

Explicação do método de substituição para sistemas de equações
O método de substituição, como o próprio nome sugere, o método consiste em substituir o valor de uma variável obtido em uma das equações do sistema e substituí-lo na outra equação.
Os sistemas de equações têm uma característica ou regra muito importante:
Quando um sistema de equação tem mais incógnitas (variáveis) que número de equações, então o sistema tem infinitas soluções, ou seja, cada variável pode assumir diferentes valores, desde que sempre satisfaça a equação. A quantidade de valores que cada variável pode assumir é infinita.
Dada a equação:
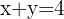
Observamos de que se trata de uma equação com duas variáveis. Podemos rapidamente identificar alguns dos valores que são solução:
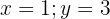
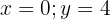
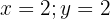
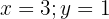

Podemos notar que, existe uma infinita quantidade de valores que podemos atribuir a  e
e  para que sejam solução.
para que sejam solução.
Por outro lado, quando o sistema tem mais equações do que incógnitas,, então o sistema tem uma única solução.
Exemplo de método de substituição
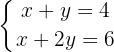
Equação I: 
Equação II: 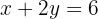
Resolvemos uma das duas variáveis em uma das duas equações (a preferência é para sempre escolher aquela que requer menos trabalho matemático para nossa conveniência). Neste caso, resolveremos  a Equação I.
a Equação I.
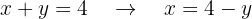
Isso é chamado "Valor de  com relação à
com relação à  "
"
A tradução para português da frase completa seria:
Substituímos o valor isolado na outra equação, neste caso, substituímos o valor de na Equação II
na Equação II

Como podemos notar, agora na equação só resta a variável isolada  . A tradução para português da frase completa seria:
. A tradução para português da frase completa seria:
Esta equação pode ser simplificada e resolvida para obter o valor de  .
.
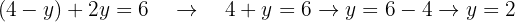
Uma vez que tenhamos o valor de uma das variáveis, neste caso o de  , podemos substituí-lo em uma das duas equações para encontrar o valor da outra variável, neste caso
, podemos substituí-lo em uma das duas equações para encontrar o valor da outra variável, neste caso  .
.
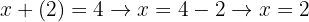
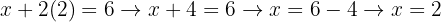
E assim obtemos o valor das nossas variáveis em um sistema de equações e observamos que a solução é ÚNICA.
Exercícios propostos do método de substituição
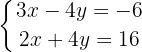
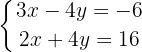 Resolvemos
Resolvemos  e a segunda equação e a simplificamos dividindo entre 2
e a segunda equação e a simplificamos dividindo entre 2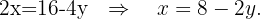
Substituímos na outra equação o valor da variável  e resolvemos a equação
e resolvemos a equação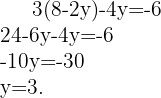
Substituimos o valor de  na segunda equação
na segunda equação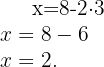
Dessa forma, o resultado do sistema de equações é:
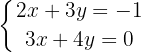
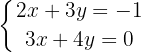
Resolvendo  da segunda equação
da segunda equação
Substituímos na outra equação a variável  e resolvemos a equação
e resolvemos a equação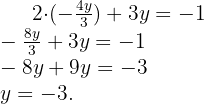
Substituimos o valor de  na segunda equação
na segunda equação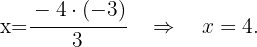
Dessa forma, a solução para o sistema de equações é
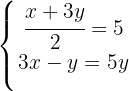
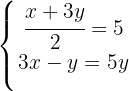
Removemos os denominadores na primeira equação multiplicando por 2 e organizamos a segunda
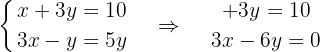
Isolamos  na segunda equação
na segunda equação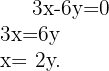
Substituímos  na outra equação
na outra equação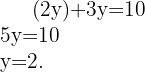
Substituímos o valor de  no
no  resolvido
resolvido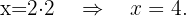
Portanto, a solução para o sistema de equações é
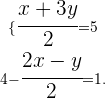
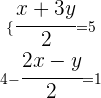
Removemos os denominadores
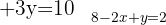
Resolvemos a segunda equação
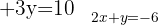
Isolamos  na primeira equação
na primeira equação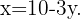
Substituímos na segunda equação e resolvemos a equação
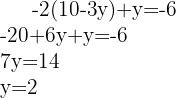
Substituimos o valor de  na primeira equação
na primeira equação
E, assim, a solução para o sistema de equações é 
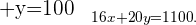
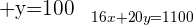
Isolamos  na primeira equação
na primeira equação 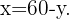
Substituímos o valor de  na outra equação e resolvemos a equação
na outra equação e resolvemos a equação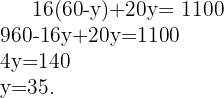
Substituimos o valor de  na primeira equação
na primeira equação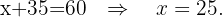
Portanto, a solução para o sistema de equações é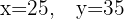
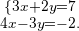
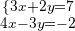
Isolamos  na primeira equação
na primeira equação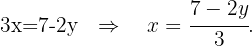
Substituímos o valor de  Substituímos na segunda equação e solucionamos a equação.
Substituímos na segunda equação e solucionamos a equação.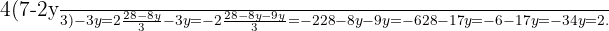
Substituímos o valor de  na primeira equação
na primeira equação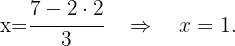
Desta forma, concluímos que a solução para o sistema de equações é
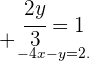
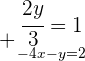
Isolamos  na primeira equação
na primeira equação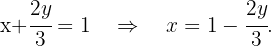
Substituímos o valor de  substituímos na segunda equação e solucionamos a equação.
substituímos na segunda equação e solucionamos a equação.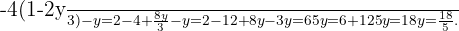
Substituimos o valor de  na primeira equação
na primeira equação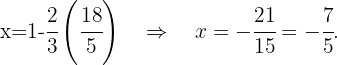
Portanto, a solução para o sistema de equações é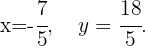
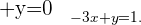

Isolamos  na primeira equação
na primeira equação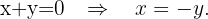
Substituímos o valor de  na outra equação e resolvemos a equação
na outra equação e resolvemos a equação
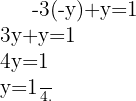
Substituimos o valor de  na primeira equação
na primeira equação
Portanto, a solução para o sistema de equações é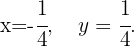
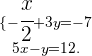
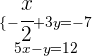
Isolamos  na primeira equação
na primeira equação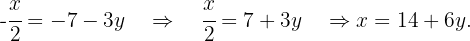
Substituímos o valor de  em outra equação e resolvemos a equação
em outra equação e resolvemos a equação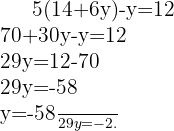
Substituímos o valor  na primeira equação
na primeira equação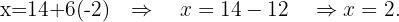
Sendo assim, a solução do sistema de equações é
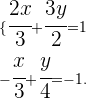
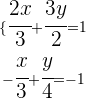
Vamos isolar  na primeira equação
na primeira equação
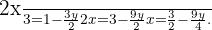
Substituímos o valor de  na outra equação e resolvemos a equação
na outra equação e resolvemos a equação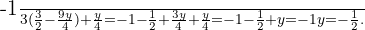
Substituímos o valor de  na primeira equação
na primeira equação
Ou seja, a solução do sistema de equações é
Resumir com IA:













