O método da comparação é uma técnica eficaz para resolver sistemas de equações lineares, especialmente aqueles que envolvem duas variáveis. Esse método se baseia em isolar uma das variáveis em ambas as equações e, em seguida, igualar as expressões obtidas. Isso nos permite encontrar um valor específico para uma das variáveis, que depois pode ser substituído para determinar o valor da outra.

Método da Comparação
O método da comparação se baseia no princípio da transitividade.
Se  e depois
e depois 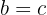 ,
,
então, por transitividade, sabe-se que  .
.
Exemplo:
Se 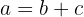 e sabemos que
e sabemos que  , então podemos afirmar que
, então podemos afirmar que 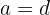 .
.
O mesmo ocorre em um sistema de equações utilizando esse método, como mostrado a seguir.
Passo 1: Selecionamos uma variável que exista em cada uma das equações do sistema.
Passo 2: Isolamos a variável em cada uma das equações.
Exemplo:
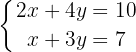
Podemos isolar qualquer das duas variáveis. Neste caso, escolhemos  . E lembre-se de fazer as operações em cada uma das duas equações.
. E lembre-se de fazer as operações em cada uma das duas equações.
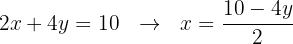

Podemos observar que em ambas equações estão igualadas a  , então por transitividade dizemos que:
, então por transitividade dizemos que:
Se  e
e 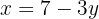 , então
, então 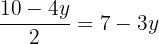 .
.
Podemos observar que agora só nos resta uma equação com uma única variável, a qual podemos simplificar e isolar, obtendo:

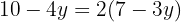
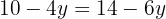

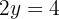

Agora, substituímos o valor de y em qualquer uma das duas equações para obter o valor de 
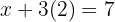
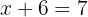


Exercícios propostos pelo método da comparação
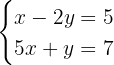
Para resolver pelo método de comparação, devemos isolar alguma variável em ambas equações. Neste caso, isolaremos  . Na primeira equação, obtemos:
. Na primeira equação, obtemos:
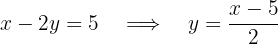
Enquanto que, para a segunda equação, obtemos:
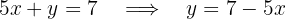
Igualando as equações, temos:

de forma que:

de modo que 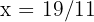 . Logo, substituindo
. Logo, substituindo  na segunda equação, temos:
na segunda equação, temos:
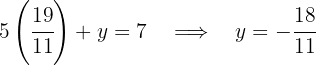
de forma que 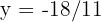 .
.
Assim, o resultado é 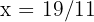 e
e 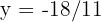 .
.

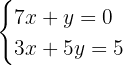
Assim como no caso anterior, para resolver por igualação, devemos isolar alguma variável em ambas as equações. Neste caso, isolaremos  . Na primeira equação, obtemos:
. Na primeira equação, obtemos:
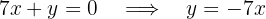
Enquanto que, para a segunda equação, obtemos:
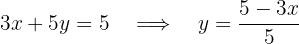
Igualando as equações, temos:
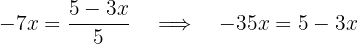
de maneira que:
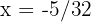 .
.
Depois, substituindo  na primeira equação, temos:
na primeira equação, temos:
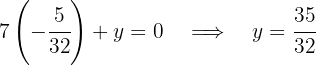
por isso 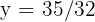 . Assim, a solução é
. Assim, a solução é 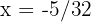 e
e 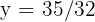 .
.
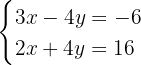
Isolamos a incógnita  na primeira e na segunda equação:
na primeira e na segunda equação:
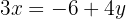

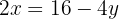
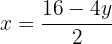
Igualamos ambas as expressões:
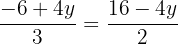
Resolvemos a equação:
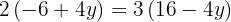
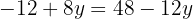
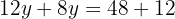


Substituímos o valor de  , em uma das duas expressões em que temos isolado
, em uma das duas expressões em que temos isolado  .
.
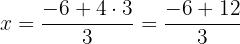

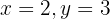
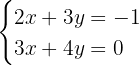
Isolamos a incógnita  da primeira e da segunda equação
da primeira e da segunda equação 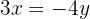
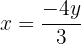
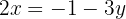
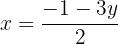
Igualamos ambas as expressões:

Resolvemos a equação:
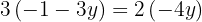
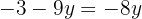
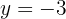
Substituímos o valor de  em uma das duas expressões em que temos isolado
em uma das duas expressões em que temos isolado 

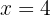
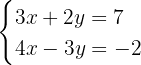
Isolamos a incógnita  da primeira e da segunda equação.
da primeira e da segunda equação.


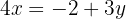

Igualamos ambas as expressões e resolvemos a equação:
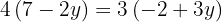
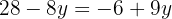
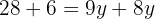
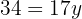

Substituímos o valor de  em uma das duas expressões em que temos a incógnita
em uma das duas expressões em que temos a incógnita  isolada.
isolada.
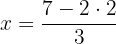

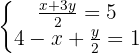
Multiplicamos a segunda equação por 2 para simplificá-la: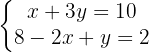
Ordenamos os termos: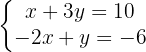
Isolamos a incógnita  na primeira e na segunda equação:
na primeira e na segunda equação: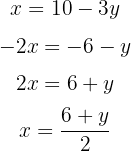
Igualamos ambas as expressões e resolvemos a equação: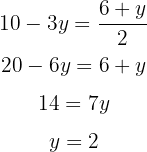
Substituímos o valor de  em uma das expressões onde
em uma das expressões onde  está isolada:
está isolada: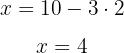

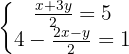
Removemos os denominadores:
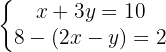
Simplificando a segunda equação:
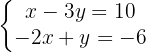
Isolamos a incógnita  da primeira e da segunda equação:
da primeira e da segunda equação:
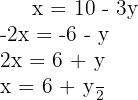
Igualamos ambas as expressões:

Resolvemos a equação:
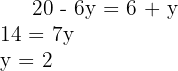
Substituindo 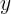 para encontrar
para encontrar 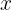
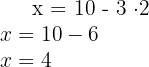
Assim,

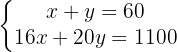
Isolamos a incógnita  na primeira e na segunda equação:
na primeira e na segunda equação:
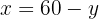
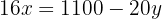
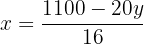
Igualamos ambas as expressões:
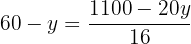
Resolvemos a equação:
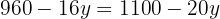
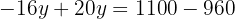

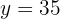
Substituímos o valor de  em uma das duas expressões em que temos a incógnita
em uma das duas expressões em que temos a incógnita  isolada.
isolada.


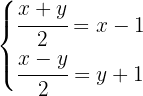
Antes de aplicar o método de comparação escrevemos o sistema de forma que uma das variáveis fique isolada. Para isso, multiplicamos ambas as equações por 2:
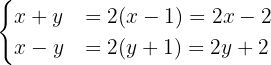
Isolamos a variável  em ambas as equações:
em ambas as equações:
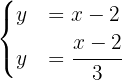
Igualando as equações, temos:
 onde:
onde:

de modo que:  . Substituindo
. Substituindo  na primeira equação, temos:
na primeira equação, temos:

Portanto, a solução é  e
e  .
.
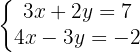
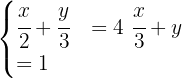
Primeiro, isolamos  em ambas as equações:
em ambas as equações:


Ao igual as equações, temos:

de forma que:

assim,  . Em seguida, substituímos
. Em seguida, substituímos  na segunda equação, temos:
na segunda equação, temos:

portanto,  . Assim, a solução é
. Assim, a solução é  e
e  .
.
Resumir com IA:












X+y=-11
-X-2y=20