
Método de redução ou eliminação
O método de redução consiste em somar ou subtrair  equações para obter uma terceira. Essa nova equação terá uma variável a menos que as anteriores, de forma que seja possível isolá-la para encontrar o valor de uma das incógnitas.
equações para obter uma terceira. Essa nova equação terá uma variável a menos que as anteriores, de forma que seja possível isolá-la para encontrar o valor de uma das incógnitas.
Exemplo:
Considerando o seguinte sistema de equações:
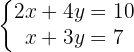
Observe que se trata de um sistema com duas equações e duas incógnitas, então podemos assumir que o sistema possui uma solução única. Assim:
Passo 1: Verificar se as duas equações podem ser somadas ou subtraídas de forma que alguma das variáveis seja eliminada.
Caso não seja possível eliminar diretamente, devemos multiplicar uma ou as duas equações por algum valor, de modo que em ambas apareça uma variável com o mesmo coeficiente.
Passo 2: Uma vez que se tenha variáveis com o mesmo coeficiente, podemos subtrair as equações para eliminar uma das variáveis.
Passo 3: Na equação resultante, isolamos a variável restante.
Passo 4: Substituímos a variável encontrada em uma das equações iniciais para descobrir o valor da outra variável.
Vamos resolver:

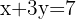
Passo 1: Como nenhuma das variáveis possui o mesmo coeficiente, vamos multiplicar a segunda equação por  :
:

Agora temos :

Passo 2: Como temos coeficientes iguais em umas das variáveis, podemos subtrair as equações:

Passo 3: Isolamos  :
:
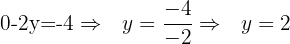
Passo 4: Substituímos  na primeira ou na segunda equação:
na primeira ou na segunda equação:

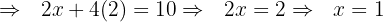
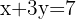

Resolva o sistema - Coeficientes inteiros
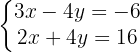
Como as duas equações tem o mesmo coeficiente na variável  mas com sinais contrários, vamos realizar a soma das duas equações:
mas com sinais contrários, vamos realizar a soma das duas equações:

Isolamos a variável para encontrar o valor:
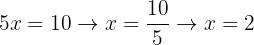
Substituímos o valor de  na segunda equação inicial:
na segunda equação inicial:
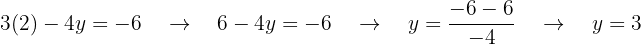
O resultado é:
 e
e 
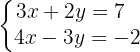
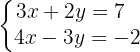
Vamos eliminar o  , para isso, multiplicamos a primeira equação por
, para isso, multiplicamos a primeira equação por  e a segunda por
e a segunda por  .
.
Somando cada parte das equações para encontrar o valor de  .
.
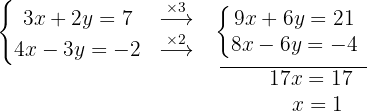
Substituímos o valor de  na primeira equação original:
na primeira equação original:
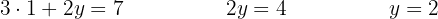
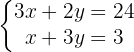
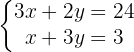
Vamos eliminar o  para isso, multiplicamos a primeira equação por
para isso, multiplicamos a primeira equação por  .
.
Somando cada parte das equações para encontrar o valor de  .
.
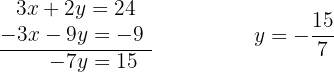
Substituímos o valor de  na segunda equação inicial.
na segunda equação inicial.
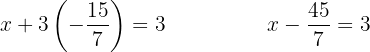
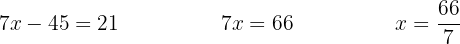
Vamos eliminar o  , para isso, multiplicamos a primeira equação por
, para isso, multiplicamos a primeira equação por  e a segunda por
e a segunda por  .
.
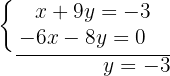
Substituímos o valor de  na segunda equação inicial.
na segunda equação inicial.

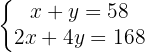
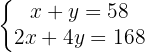
Vamos eliminar  multiplicando a primeira equação por
multiplicando a primeira equação por 
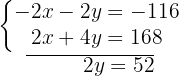
Calculamos o valor de 
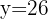
Substituímos o valor de  na primeira equação.
na primeira equação.

Resolva o sistema - Coeficientes racionais
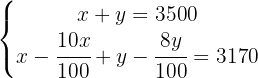
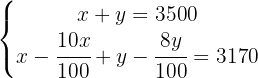
Eliminamos os denominadores na segunda equação multiplicando  por
por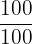 .
.
Essa fração é igual a  , portanto não altera a equação, é apenas de um truque para facilitar os cálculos.
, portanto não altera a equação, é apenas de um truque para facilitar os cálculos.
Obtemos:
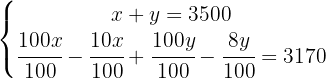
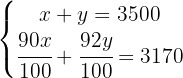
Para eliminar os denominadores da segunda equação, multiplicamos 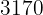 por
por  . E fica assim:
. E fica assim:
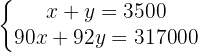
Vamos empregar o método da redução. Para isso, precisamos eliminar uma das duas incógnitas ao somar as equações. Podemos multiplicar a primeira equação por 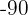 e assim eliminar o
e assim eliminar o  .
.
Somando as duas equações, obteremos uma equação com uma única incógnita (a variável  )
)
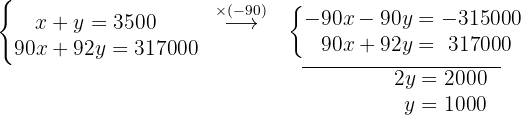
Obtemos o valor de 

Substituímos o valor de  na primeira equação original:
na primeira equação original:

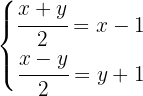
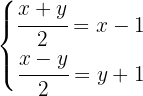
Eliminamos os denominadores. Para isso, multiplicamos as equações por  , já que esse é o único denominador presente em ambas:
, já que esse é o único denominador presente em ambas:
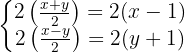
Como, do lado esquerdo das equações, estamos multiplicando e dividindo pelo mesmo número, o 2 é cancelado:
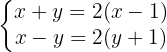
Removemos os parênteses:
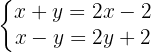
Organizamos os termos: variáveis de um lado e termo independente do outro:
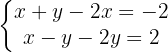
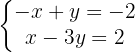
Como temos  e
e  nas equações, podemos aplicar diretamente o método da redução (somando as equações), pois a variável
nas equações, podemos aplicar diretamente o método da redução (somando as equações), pois a variável  será eliminada porque
será eliminada porque 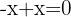
Somamos membro a membro e calculamos o valor de  .
.
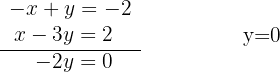
Substituímos o valor de  na segunda equação do sistema (também poderíamos usar a primeira) e isolamos:
na segunda equação do sistema (também poderíamos usar a primeira) e isolamos:
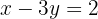


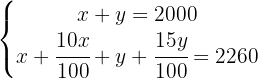
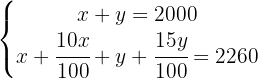
Eliminamos os denominadores da segunda equação multiplicando por 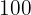 , já que é o único denominador que aparece:
, já que é o único denominador que aparece:


Cancelamos o 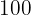 nos termos onde ele está multiplicando e dividindo, já que:
nos termos onde ele está multiplicando e dividindo, já que: 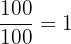
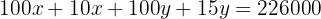
Somamos os termos semelhantes para simplificar:
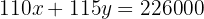
Vamos a eliminar  . Para isso, multiplicamos a primeira equação por
. Para isso, multiplicamos a primeira equação por 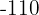
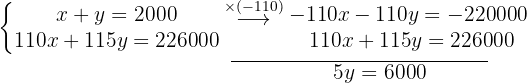
Obtemos o valor de  .
.
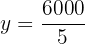

Substituímos o valor de  na primeira equação e isolamos.
na primeira equação e isolamos.


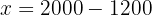
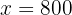
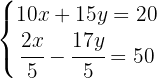
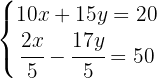
Começamos pela eliminação dos denominadores da segunda equação. Fazemos isso multiplicando a segunda equação por  :
:
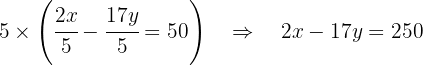
Agora, multiplicamos esta última equação por  :
:
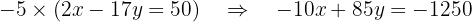
Em seguida, somamos essa equação com a primeira para eliminar  :
:
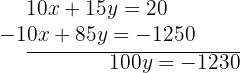
Logo, temos que:
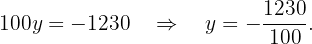
Ou seja,
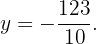
Agora, substituímos esse valor de  em qualquer uma das duas equações para encontrar o valor de
em qualquer uma das duas equações para encontrar o valor de  . Por exemplo, substituímos na primeira equação e simplificamos:
. Por exemplo, substituímos na primeira equação e simplificamos:

E essa é a solução do sistema de equações:
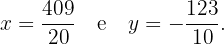
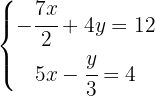
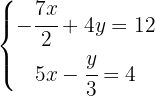
Começamos por eliminar os denominadores das equações. Para isso, multiplicamos a primeira equação por  e a segunda por
e a segunda por  :
:
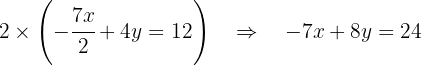
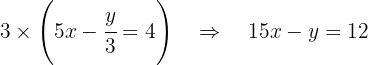
Agora, multiplicamos esta última equação por  :
:
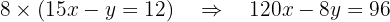
Agora, somamos as equações para eliminar a variável  :
:
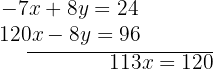
Portanto, temos que:
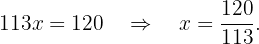
Agora, substituímos o valor de  qualquer uma das duas equações para encontrar o valor de
qualquer uma das duas equações para encontrar o valor de  . Por exemplo, substituímos na primeira equação e simplificamos:
. Por exemplo, substituímos na primeira equação e simplificamos:

E essa é a solução do sistema de equações:
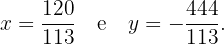
Resumir com IA:












