Temas

Resolução por substituição e método gráfico
Resolva o seguinte sistema utilizando o método pela substituição e o método gráfico

1. Começamos resolvendo o sistema por substituição:
O método pela substituição consiste em isolar uma das duas variáveis de uma das equações e substituí-la em outra. Isolamos  da segunda equação:
da segunda equação:

Note que escolhemos a segunda equação já que está igualada a 0; isso faz com que o procedimento seja mais fácil. Agora substituímos o valor de  na primeira equação
na primeira equação

Portanto,  . Assim, substituímos o valor de
. Assim, substituímos o valor de  na expressão de
na expressão de  :
:

Portanto, a solução é  .
.
2. Agora resolvemos o sistema pelo método gráfico:
O método gráfico consiste em fazer um gráfico para as duas retas. A interseção será a solução do sistema:
Com o gráfico anterior podemos observar que a solução é  e
e  . Além disso, devemos lembrar que precisamos ser muito precisos na hora de fazer o gráfico.
. Além disso, devemos lembrar que precisamos ser muito precisos na hora de fazer o gráfico.
Resolva o seguinte sistema utilizando o método pela substituição:

Uma vantagem do método pela substituição é que com ele não precisamos simplificar o sistema de equações antes de começar a resolver. Portanto, podemos começar a resolver imediatamente.
Primeiro, isolamos  da segunda equação:
da segunda equação:
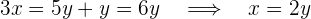
Depois, substituímos o valor de  na primeira equação:
na primeira equação:

A partir daqui, sabemos que  . Agora, substituímos o valor de
. Agora, substituímos o valor de  na expressão anterior de
na expressão anterior de  :
:

Portanto, a solução do sistema é  e
e  .
.
Calcule o domínio das funções exponenciais:
a) 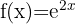
b) 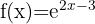
c) 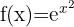
d) 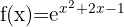
e) 
O domínio de uma função exponencial é 
1 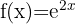

2 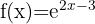

3 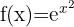

4 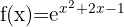

5 
Como o expoente é racional,  não pertence ao domínio porque anula o denominador. Portanto,
não pertence ao domínio porque anula o denominador. Portanto, 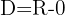 .
.
Resolução por igualdade
Devemos lembrar que o método pela igualdade pode ser utilizado apenas para resolver um sistema de 2 equações com 2 variáveis. Apenas este método e o método gráfico estão limitados para os sistemas de  .
.
Resolva o seguinte sistema de equações utilizando o método pela igualdade:

Para resolver o sistema por igualdade devemos isolar uma variável de ambas equações. Isolamos  de ambas equações:
de ambas equações:

onde obtemos  . Para a segunda equação temos
. Para a segunda equação temos

portanto  e
e  . Agora, igualamos ambas equações
. Agora, igualamos ambas equações

Dessa equação isolamos  :
:

assim  . Dessa forma, substituímos o valor de
. Dessa forma, substituímos o valor de  na primeira equação
na primeira equação

assim  . Portanto, a solução é
. Portanto, a solução é  e
e  .
.
Utilizando o método pela igualdade, resolva o seguinte sistema de equações:

Da mesma maneira que no caso anterior, para resolver por igualdade devemos isolar alguma variável de ambas equações. Neste caso, vamos isolar  . Na primeira equação obtemos:
. Na primeira equação obtemos:

Enquanto que para a segunda equação obtemos:

Igualando as equações, temos

assim

de modo que  . Assim, substituindo
. Assim, substituindo  na primeira equação, temos
na primeira equação, temos

dessa forma  . Assim, a solução é
. Assim, a solução é  e
e  .
.
Calcule o domínio das funções logarítmicas:
a) 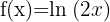
b) 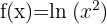
c) 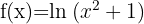
d) 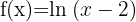
e) 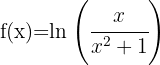
Para que a função logaritmo esteja bem definida, seu argumento deve ser positivo, ou seja, seu domínio é 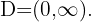
a) 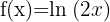
Resolvemos 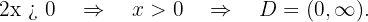
b) 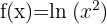
Como  é sempre positivo para
é sempre positivo para 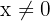 , então
, então 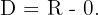
c) 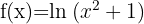
Como 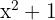 é sempre positivo, então
é sempre positivo, então 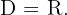
d) 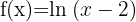
Resolvemos 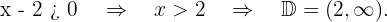
e) 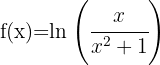
Como o denominador é sempre positivo, estudamos apenas o numerador. Assim,
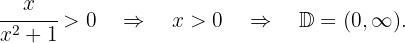
Resolução por redução
Devemos lembrar que com o método pela redução devemos eliminar os  de todas as equações, exceto a primeira. Depois, devemos eliminar os
de todas as equações, exceto a primeira. Depois, devemos eliminar os  de todas as equações, exceto a primeira e a segunda equação.
de todas as equações, exceto a primeira e a segunda equação.
Este método é igual a Eliminação gaussiana, com a única diferença de que não utilizamos a matriz associada ao sistema.
Resolva o seguinte sistema utilizando o método pela redução:

Precisamos eliminar os  da segunda equação. Para isso, multiplicamos a primeira equação por
da segunda equação. Para isso, multiplicamos a primeira equação por  e depois subtraímos o resultado na segunda equação:
e depois subtraímos o resultado na segunda equação:

Agora, calculamos a segunda equação com a equação anterior:

A partir daqui sabemos que  . Depois, substituímos o valor de
. Depois, substituímos o valor de  na primeira equação:
na primeira equação:

Portanto  .
.
Observe que o sistema é o mesmo do primeiro exercício e obtemos a mesma solução apesar de utilizar um método diferente.
Resolva o seguinte sistema utilizando o método pela redução:

Antes de aplicar o método pela redução, devemos escrever o sistema de forma que os termos independentes estejam do lado direito. Para isso, multiplicamos ambas equações por 2:

Depois, passamos as variáveis para o lado esquerdo das equações:

Agora, somamos a primeira equação na segunda equação:

A partir daqui sabemos que  . Depois, substituímos o valor de
. Depois, substituímos o valor de  na primeira equação:
na primeira equação:

Portanto, a solução é  e
e  .
.
Calcular o domínio das funções trigonométricas:
a) 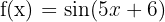
b) 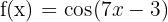
c) 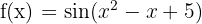
d) 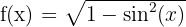
e) 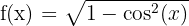
a) 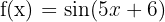
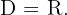
b) 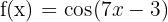
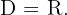
c) 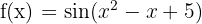
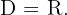
O domínio de uma função irracional de índice par é formado pelos valores que tornam o radicando maior ou igual a zero. As funções trigonométricas seno e cosseno têm como domínio todos os números reais. Além disso, seu valor máximo é 1, o que garante que essas funções sempre terão valores menores ou iguais a 1 para qualquer número real.
d) 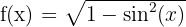
Resolvemos 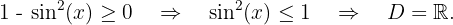
e) 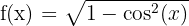
Resolvemos 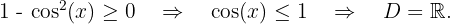
Resolução utilizando qualquer método
Resolva o seguinte sistema utilizando qualquer método:

Podemos resolver o sistema utilizando a substituição. Primeiro isolamos  da segunda equação
da segunda equação

Depois, substituímos o valor de  na primeira equação:
na primeira equação:

Portanto, a primeira equação se converte (ao passarmos as constantes para o lado direito e as variáveis para o lado esquerdo) em

que, ao isolar  , obtemos
, obtemos

Depois, substituindo o valor de  na expressão de
na expressão de  , obtemos
, obtemos

Portanto, a solução é  e
e 
Encontre as soluções do seguinte sistema:

Para resolver este sistema, primeiro devemos eliminar as frações (retirar os denominadores). Para isso, multiplicamos as equações pelo mínimo múltiplo comum dos denominadores. Para a primeira equação temos:

assim  . Enquanto que para a segunda equação temos:
. Enquanto que para a segunda equação temos:

onde obtemos  . Assim, o sistema de equações se converte em:
. Assim, o sistema de equações se converte em:

Agora resolvemos o sistema da maneira que desejamos. Aqui utilizaremos o método pela substituição. Assim, primeiro isolamos  da segunda equação:
da segunda equação:

Depois, substituímos o valor de  na primeira equação:
na primeira equação:

de modo que  o
o  . Depois, substituímos o valor de
. Depois, substituímos o valor de  na expressão de
na expressão de  :
:

Portanto, a solução é  e
e  .
.
Resumir com IA:












