Exercícios de representação de funções algébricas

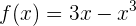
Dominio
Lembramos que, dependendo do tipo de função, podemos determinar o domínio. Neste caso 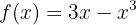, trata-se de uma função polinomial, então seu domínio são todos os números reais, isto é, .

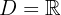Simetria
Para analisar a simetria, começamos avaliando a função em , e teremos três possíveis casos:

1 A função é par se ,
2 A função é ímpar se ,
3 Ou não se aplica se não retornarmos à função original.

Neste caso:

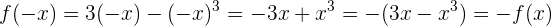
Portanto, temos simetria em relação à origem, isto é, é uma função ímpar.

Pontos de corte com os eixos
Pontos de corte com :

Temos corte nesse eixo quando 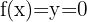. Então começamos igualando a zero:

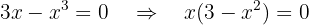
Portanto, obtemos zero quando:

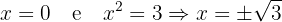
Assim, os pontos de corte com o eixo são:

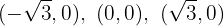
Ponto de corte com :

Há corte nesse eixo quando . Então:

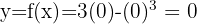
Portanto, o ponto de corte com o eixo é:

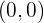
Assíntotas
Para encontrar as assíntotas, precisaríamos de um ponto tal que .

Neste caso, temos uma função polinomial e, portanto,  não possui assíntotas.

Crescimento e decrescimento
Para saber se uma função é crescente ou decrescente em um ponto, devemos encontrar os pontos críticos, ou seja, onde a derivada se anula. Calculamos a derivada :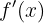

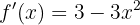
Vamos calcular os pontos críticos

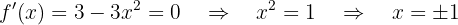
Agora vamos analisar o sinal da função ao dividir o domínio em:

e :

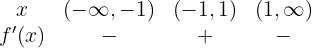
Assim, a função é crescente no intervalo:

e decrescente em

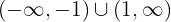
Para encontrar mínimos e máximos, avaliamos os pontos críticos na segunda derivada. Se o valor for positivo, temos um mínimo; se for negativo, temos um máximo.

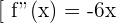
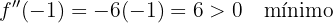
e máximo em

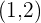
Concavidade e convexidade

Para analisar concavidade e convexidade, usamos a segunda derivada e verificamos onde ela se anula. Depois analisamos os intervalos onde é positiva ou negativa: se for positiva, a função é convexa; se for negativa, é côncava.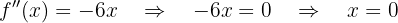

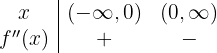
Então, a função é convexa no intervalo 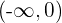e côncava em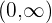

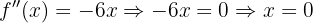
Pontos de inflexão
Há um ponto de inflexão em quando:

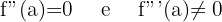
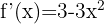
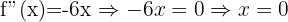
Agora avaliamos o único ponto onde a segunda derivada se anula:

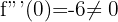
Como o resultado é diferente de zero, temos um ponto de inflexão em:

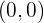
Representação gráfica

 

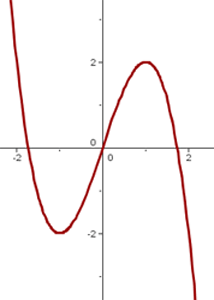
Dominio
.

Simetria
Observamos que:

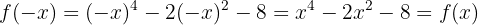
Portanto, temos simetria em relação ao eixo , ou seja, a função é par.

Pontos de corte com os eixos

Pontos de corte com :

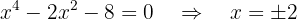
Então, os pontos de corte são:

Pontos de corte com :

Notamos que:

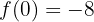
Então, o ponto de corte é:

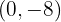
Assíntotas
Não possui assíntotas.

Crescimento e decrescimento
Calculamos os pontos críticos:

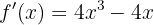
Igualamos a zero:

Agora verificamos o sinal ao segmentar o domínio:

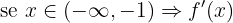
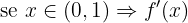
Portanto, a função é crescente em e decrescente em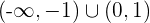

Avaliando os pontos críticos na segunda derivada 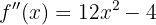, obtemos que:

Os pontos mínimos são:

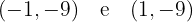
E como ponto máximo temos:

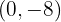
Concavidade e convexidade
Buscamos os pontos onde a segunda derivada se anula:

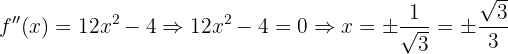
Observamos que:

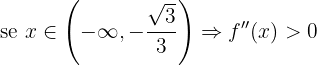
Portanto, a função é convexa em

e côncava em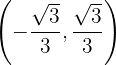
.

Pontos de inflexão
Calculando a terceira derivada, concluímos que os pontos de inflexão são:

Representação gráfica

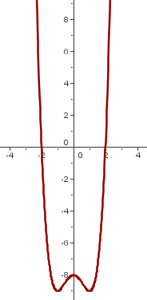
Dominio
Eliminamos o ponto onde o denominador se anula: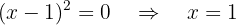

portanto,

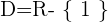
Simetria
Notamos que:

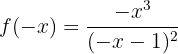
ou seja, a função não apresenta simetria.

Pontos de corte com os eixos:

Pontos de corte com :

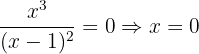
Então, o ponto de corte é:

Ponto de corte com :
Temos que:

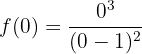
Então, o ponto de corte é:

Assíntotas

Assíntota horizontal:
As assíntotas horizontais são retas horizontais às quais a função se aproxima indefinidamente. Elas têm equação: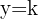

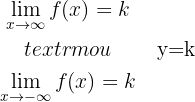
Notamos que:

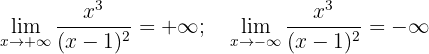
Então, não possui assíntota horizontal.

Assíntota vertical:
Assíntotas verticais são retas verticais às quais a função se aproxima indefinidamente sem nunca cortar. Elas têm equação:

Notamos que:

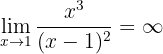
Portanto:

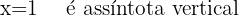
Assíntota oblíqua:
As assíntotas oblíquas têm equação:

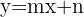
onde:

Só buscamos assíntotas oblíquas quando não existe assíntota horizontal.

Neste caso:

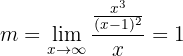
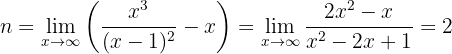
Assim, a assíntota oblíqua é:

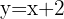
Crescimento e decrescimento
Primeiro encontramos os pontos críticos:

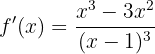
Igualando a zero:

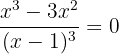
Teremos como pontos críticos:

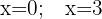
Agora verificamos os sinais ao segmentar o domínio:

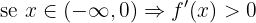
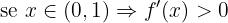
Portanto:

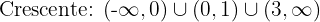
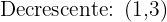
Avaliando os pontos críticos na segunda derivada, obtemos:

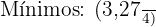
Concavidade e convexidade
Calculamos a segunda derivada e encontramos onde ela se anula:

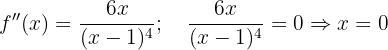
Avaliando nos intervalos:

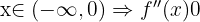
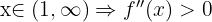
Portanto, a função é convexa em
e côncava en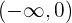

Pontos de inflexão

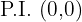
Representação gráfica

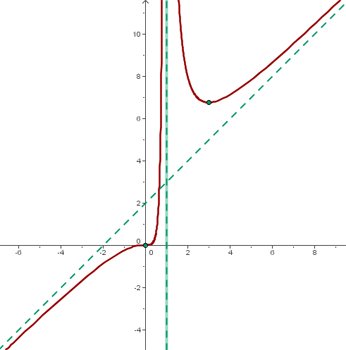
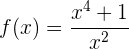
Domínio
Eliminamos o ponto onde o denominador se anula

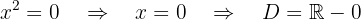
Simetria
Notamos que

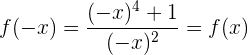
Portanto, a função apresenta simetria em relação ao eixo . É uma função par.

Pontos de corte com os eixos

Corte com o eixo :
Igualamos a função a zero:

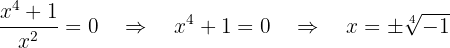
Como essa equação não tem solução real, não há pontos de corte com o eixo .

Corte com o eixo :
Analisando:

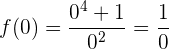
A expressão é indefinida, portanto não há ponto de corte com o eixo .

Assíntotas

Assíntota horizontal: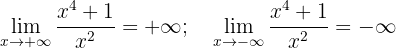

Logo, não existe assíntota horizontal.

Assíntota vertical: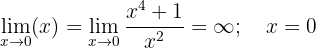

Assim, existe assíntota vertical em .

Assíntota oblíqua: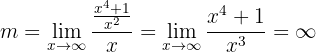

Portanto, a função não possui assíntota oblíqua.

Crescimento e decrescimento
Observamos que

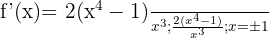
A análise de sinais mostra:

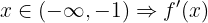
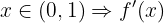
Portanto, a função é:

crescente em
decrescente em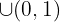

Os pontos mínimos são: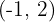
e

Concavidade e convexidade
A segunda derivada é:

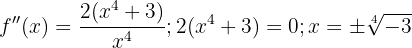
Como não há solução real para o termo entre parênteses, usamos a análise de sinais:

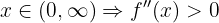
Logo, a função é convexa em todo o domínio, isto é, em: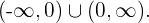

Pontos de inflexão
Não existe ponto de inflexão.

Representação gráfica

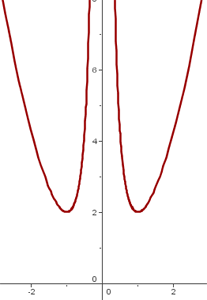
Domínio
Eliminamos o ponto onde o denominador se anula:

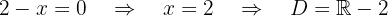
Simetria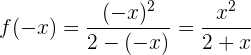

A função não apresenta simetria.

Pontos de corte com os eixos

Ponto de corte com :

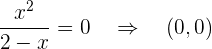
Ponto de corte com :

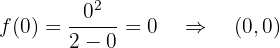
Assíntotas

Assíntota horizontal:
Notamos que

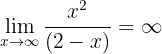
Portanto, não possui assíntota horizontal.

Assíntota vertical: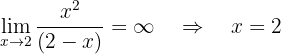

Assíntota oblíqua: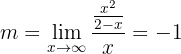

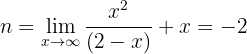
Assim, a assíntota oblíqua é:

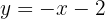
Crescimento e decrescimento
Encontramos os pontos críticos:

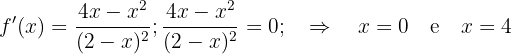
Avaliando os intervalos:

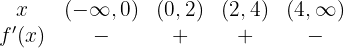
Portanto, a função é crescente em: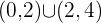 e decrescente em: .

Avaliando os pontos críticos na segunda derivada, obtemos:

Temos que es mínimo e 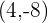  máximo.

Concavidade e convexidade

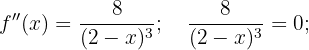
Como não há solução, dividimos o domínio considerando o ponto 2, que não pertence ao domínio.

Assim:

Portanto, a função é: 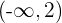convexa e  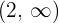côncava.

Pontos de inflexão
Não há ponto de inflexão.

Representação gráfica

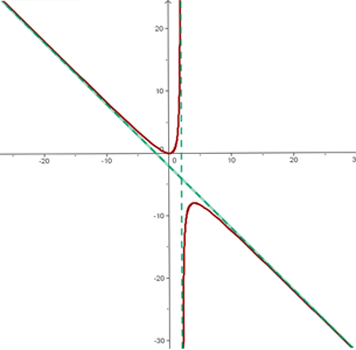
Domínio

Simetria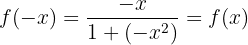

Temos simetria em relação à origem, ou seja, trata-se de uma função ímpar.

Pontos de corte com os eixos

Ponto de corte com :

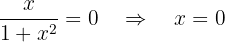
Então, o ponto de corte é:

Ponto de corte com :

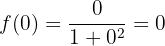
Portanto, o ponto de corte é:

Assíntotas

Assíntota horizontal:

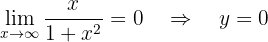
A função não possui assíntotas verticais nem oblíquas.

Crescimento e decrescimento

Encontramos os pontos críticos:

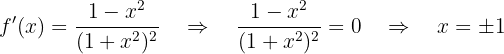
Avaliando o sinal em cada intervalo do domínio:

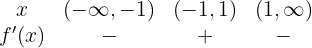
Assim, a função é crescente em latex[/latex]
e decrescente em .

Avaliando os pontos críticos na segunda derivada:

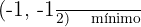
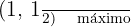
Concavidade e convexidade

Calculamos os pontos onde a segunda derivada se anula:

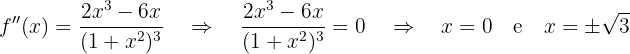
Agora analisamos os intervalos:

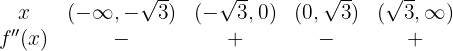
Portanto, a função é convexa em côncava em .

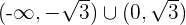Pontos de inflexão

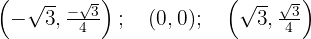
Representação gráfica

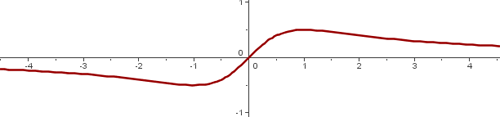
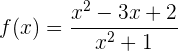
Domínio

Simetria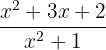

A função não apresenta simetria.

Pontos de corte com os eixos

Pontos de corte com :

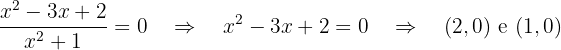
Ponto de corte com :

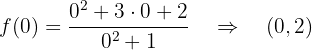
Assíntotas

Assíntota horizontal:

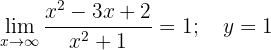
A função não apresenta assíntotas verticais nem oblíquas.

Crescimento e decrescimento

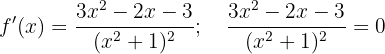
Assim, os pontos críticos são:

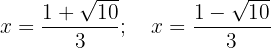
Analisamos o sinal da derivada nos intervalos:

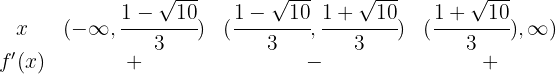
Portanto, a função é:

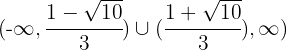y decreciente de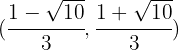

 

Avaliando os pontos críticos na segunda derivada, obtemos:

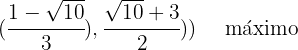
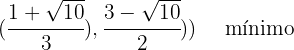
Representação gráfica

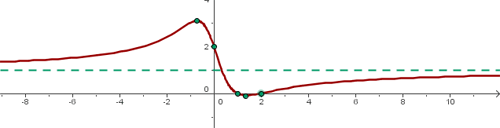
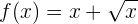
Domínio
Como a função envolve raiz de , temos:

Simetria

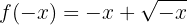
A função não apresenta simetria.

Pontos de corte com os eixos

Ponto de corte com :

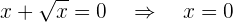
Portanto, o ponto de corte é:

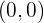
Ponto de corte com :

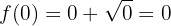
Portanto, o ponto de corte é:

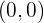
Assíntotas
A função não possui assíntotas.

Crescimento e decrescimento

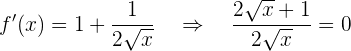
Assim, os pontos críticos viriam de:

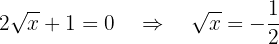
Como não há solução, analisamos apenas o intervalo do domínio:

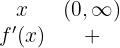
Portanto, a função é crescente em todo o domínio.

Máximos e mínimos
A função não possui extremos locais.

Concavidade e convexidade

Calculamos a segunda derivada e igualamos a zero:

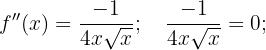
Como não há solução, analisamos o intervalo do domínio:

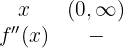
Portanto, a função é côncava.

Pontos de inflexão
A função não possui ponto de inflexão.

Representação gráfica

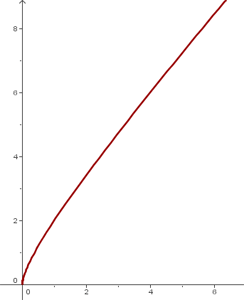
Domínio

Simetria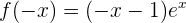

A função não apresenta simetria.

Pontos de corte com os eixos

Ponto de corte com :

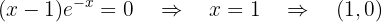
Ponto de corte com :

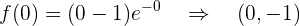
Assíntotas

Assíntota horizontal: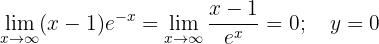

A função não possui assíntotas verticais nem oblíquas.

Crescimento e decrescimento

Verificando o sinal:

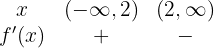
De onde podemos deduzir que a função é crescente de 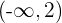e decrescente de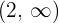

Avaliando o ponto crítico na segunda derivada, obtemos:

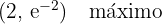
Concavidade e convexidade

Calculamos a segunda derivada e encontramos os pontos que a anulam:

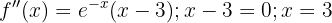
Segmentamos o domínio em e verificamos o sinal:

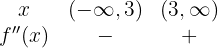
Portanto, a função no intervalo é convexa e no intervalo é côncava.

Pontos de inflexão

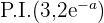
Representação gráfica

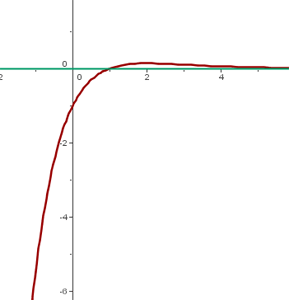
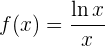
Domínio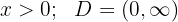

Simetria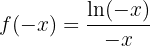

A função não apresenta simetria.

Pontos de corte com os eixos

Ponto de corte com :

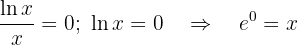
Assim, e o ponto de corte é:

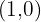
Ponto de corte com :

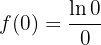
A função não corta o eixo .

Assíntotas

Assíntota horizontal: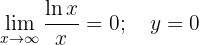

Assíntota vertical: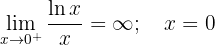

Crescimento e decrescimento

Calculamos os pontos críticos:

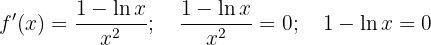
O ponto crítico é:

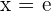
Analisando os intervalos:

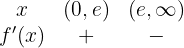
Portanto:

• a função é crescente em 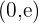e decrescente em . Encontramos um máximo em .

Concavidade e convexidade

Igualando a segunda derivada a zero:

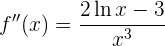
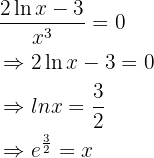
Segmentando o dominio e observando o sinal da segunda derivada concluímos que a função é convexa de e côncava de .

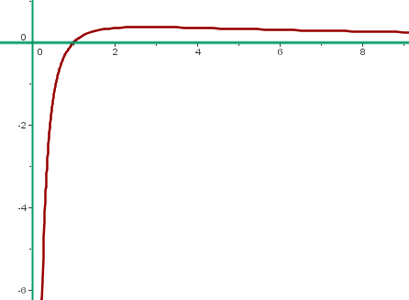
Representação gráfica