As progressões aritméticas são uma sequência de números em que cada termo, após o primeiro, é obtido somando uma constante, conhecida como razão comum, ao termo anterior. Esse tipo de sequência é fundamental na matemática e é aplicado em diversas áreas, como economia, estatística e programação.
Neste artigo, apresentaremos uma série de exercícios resolvidos que ilustram os conceitos-chave das progressões aritméticas, desde a identificação de termos até a soma de sequências.
O quarto termo de uma progressão aritmética é  , e o sexto é
, e o sexto é  . Escreva a progressão.
. Escreva a progressão.
a. Os dados que sabemos sobre a progressão são:
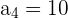 e
e 
b. Uma progressão aritmética obedece à expressão:
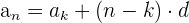
c. Substituímos os dados e obtemos a diferença " " entre os termos da progressão:
" entre os termos da progressão:
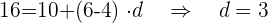
d. Obtemos o valor do primeiro termo da progressão:
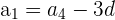

e. A progressão aritmética é:
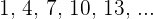
O segundo termo de uma progressão aritmética é  , e o sétimo é
, e o sétimo é  . Escreva a progressão.
. Escreva a progressão.
a. Os dados que sabemos sobre a progressão são:
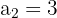 e
e 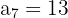
b. Uma progressão aritmética obedece à expressão:
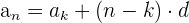
c. Substituímos os dados e obtemos a diferença " " entre os termos da progressão:
" entre os termos da progressão:
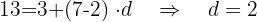
d. Obtemos o valor do primeiro termo da progressão:
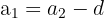
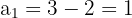
e. A progressão aritmética é:
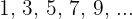
O quinto termo de uma progressão aritmética é  , e o nono é
, e o nono é  . Escreva a progressão.
. Escreva a progressão.
a. Os dados que sabemos sobre a progressão são:
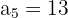 e
e 
b. Uma progressão aritmética obedece à expressão:
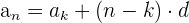
c. Substituímos os dados e obtemos a diferença " " entre os termos da progressão:
" entre os termos da progressão:
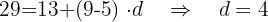
d. Obtemos o valor do primeiro termo da progressão:
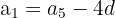

e. A progressão aritmética é:
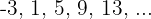
O termo 20 de uma progressão aritmética é  , e o termo 35 é
, e o termo 35 é  . Escreva a progressão.
. Escreva a progressão.
a. Os dados que sabemos sobre a progressão são:
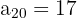 e
e 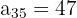
b. Uma progressão aritmética obedece à expressão:
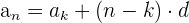
c. Substituímos os dados e obtemos a diferença " " entre os termos da progressão:
" entre os termos da progressão:
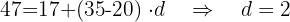
d. Obtemos o valor do primeiro termo da progressão:
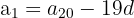
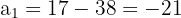
e. A progressão aritmética é:
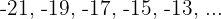
O termo 40 de uma progressão aritmética é 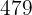 , e o termo 85 é
, e o termo 85 é 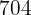 . Escreva a progressão.
. Escreva a progressão.
a. Os dados que sabemos sobre a progressão são:
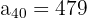 e
e 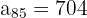
b. Uma progressão aritmética obedece à expressão:
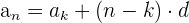
c. Substituímos os dados e obtemos a diferença " " entre os termos da progressão:
" entre os termos da progressão:
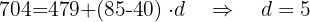
d. Obtemos o valor do primeiro termo da progressão:
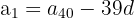
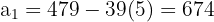
e. A progressão aritmética é:
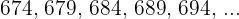
Escreva três meios aritméticos entre  e
e 
a. Os dados que temos são:
 e
e 
b. Para encontrar a diferença entre os termos da progressão, utiliza-se a fórmula:
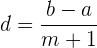
c. Substituímos e resolvemos:

d. A progressão é:

Escreva três meios aritméticos entre 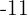 e
e 
a. Os dados que temos são:
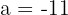 e
e 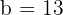
b. Para encontrar a diferença entre os termos da progressão, utiliza-se a fórmula:
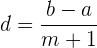
c. Substituímos e resolvemos:
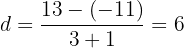
d. A progressão é:
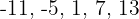
Faça a interpolação dos três meios aritméticos entre  e
e 
a. Os dados que temos são:
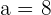 e
e 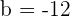
b. Para encontrar a diferença entre os termos da progressão, utiliza-se a fórmula:
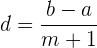
c. Substituímos e resolvemos:
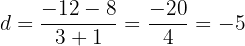
d. A progressão é:
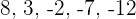
Interpole quatro meios aritméticos entre  e
e 
a. Os dados que dispomos são:
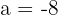 e
e 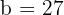
b. Para encontrar a diferença entre os termos da progressão, utiliza-se a fórmula:
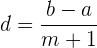
c. Substituímos e resolvemos:
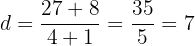
d. A progressão é:
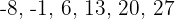
Faça a interpolação de quatro meios aritméticos entre  e
e 
a. Os dados que temos são:
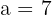 e
e 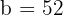
b. Para encontrar a diferença entre os termos da progressão, utiliza-se a fórmula:
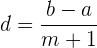
c. Substituímos e resolvemos:
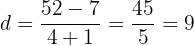
d. A progressão é:
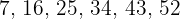
O primeiro termo de uma progressão aritmética é  , e o décimo quinto é
, e o décimo quinto é  . Determine a diferença e a soma dos quinze primeiros termos.
. Determine a diferença e a soma dos quinze primeiros termos.
a. Os dados que temos são:
 e
e 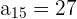
b. Em uma progressão aritmética, temos:
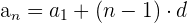
c. Substituímos os dados:
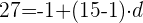
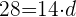
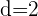
d. A diferença entre os termos é 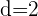
e. Para calcular a soma dos primeiros  termos, usamos a fórmula:
termos, usamos a fórmula:
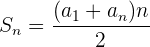
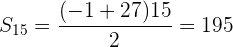
O primeiro termo de uma progressão aritmética é  e o quinto termo é
e o quinto termo é  . Determine a soma dos cinco primeiros termos.
. Determine a soma dos cinco primeiros termos.
a. Os dados que temos são: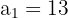 e
e 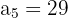
b. Em uma progressão aritmética, vale a seguinte fórmula: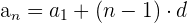
c. Substituindo os dados: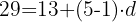
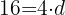
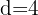
d. A diferença entre os termos é 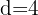 .
.
e. Para calcular a soma dos primeiros  termos, usamos a fórmula:
termos, usamos a fórmula: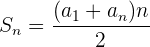
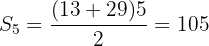
Determine a soma dos quinze primeiros múltiplos de  .
.
a. Os dados que temos são: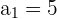 ,
, 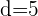 e
e 
b. Em uma progressão aritmética, vale a seguinte fórmula: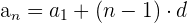
c. Substituindo os dados para obter o décimo quinto termo:
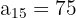
d. Para calcular a soma dos primeiros  termos, usamos a fórmula:
termos, usamos a fórmula: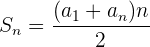

Determine a soma dos quinze primeiros números terminados em  .
.
a. Os dados que temos são: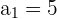 ,
, 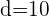 e
e 
b. Em uma progressão aritmética, vale a seguinte fórmula: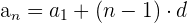
c. Substituindo os dados para obter o décimo quinto termo:
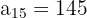
d. Para calcular a soma dos primeiros  termos, usamos a fórmula:
termos, usamos a fórmula: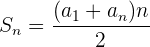

Determine a soma dos quinze primeiros números pares maiores que  .
.
a. Os dados que temos são: ,
, 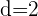 e
e 
b. Em uma progressão aritmética, vale a seguinte fórmula: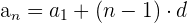
c. Substituindo os dados para obter o décimo quinto termo: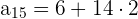
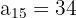
d. Para calcular a soma dos primeiros  termos, usamos a fórmula:
termos, usamos a fórmula: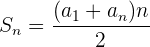
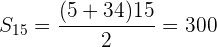
Determine os ângulos de um triângulo, sabendo que estão em progressão aritmética e que 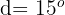 .
.
a. A soma dos ângulos internos de um triângulo é 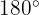 . Substituindo na fórmula:
. Substituindo na fórmula: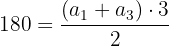
b. Entre o primeiro e o terceiro termo, temos a relação: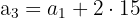
c. Substituindo: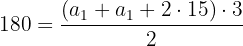
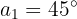
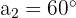
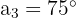
Determine os ângulos de um quadrilátero convexo, sabendo que estão em progressão aritmética e que 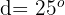 .
.
a. A soma dos ângulos internos de um quadrilátero é 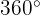 :
: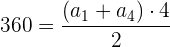
b. Entre o primeiro e o quarto termo, temos a relação:
c. Substituindo: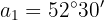
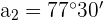
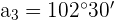

O cateto menor de um triângulo retângulo mede  cm. Calcule os outros dois lados, sabendo que formam uma progressão aritmética.
cm. Calcule os outros dois lados, sabendo que formam uma progressão aritmética.
a. Calculamos os outros dois lados sabendo que os dois lados do triângulo formam uma progressão aritmética.


b. Aplicamos o Teorema de Pitágoras
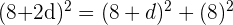
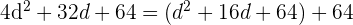

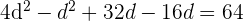
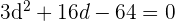
c. Resolvemos através da formula de equações de segundo grau:
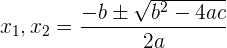
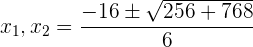
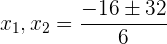

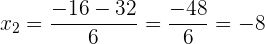
d. Uma vez que o resultado não pode dar negativo, obtemos:
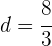
e. O resultado negativo não é válido porque o comprimento dos lados de um triângulo deve ser positivo.

Calcule três números em progressão aritmética, cuja soma é  e cuja soma de seus quadrados é
e cuja soma de seus quadrados é 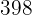 .
.
a. Consideremos que o termo central seja  .
.
b. O primeiro termo pode ser expresso como:  .
.
c. O terceiro termo pode ser expresso como: 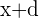 .
.
d. A soma dos três termos é  , então:
, então: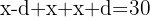
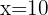
e. A soma dos quadrados dos  números é
números é 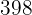 , então podemos escrever:
, então podemos escrever: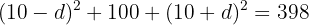
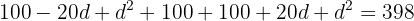
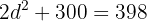
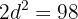
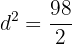
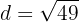
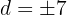
f. Temos duas progressões que satisfazem a condição (uma para o valor positivo de ' ' e outra para o valor negativo):
' e outra para o valor negativo):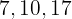
Calcule três números em progressão aritmética, cuja soma é  e cuja soma de seus quadrados é
e cuja soma de seus quadrados é 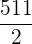 .
.
a. Vamos considerar que o termo central seja  .
.
b. O primeiro termo pode ser expresso como:  .
.
c. O terceiro termo pode ser expresso como: 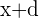 .
.
d. A soma dos três termos é  , então:
, então:

e. A soma dos quadrados dos  números é
números é 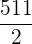 , então podemos escrever:
, então podemos escrever:

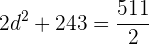
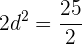

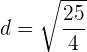
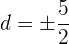
f. Temos duas progressões que satisfazem a condição (uma para o valor positivo de ' ' e outra para o valor negativo):
' e outra para o valor negativo):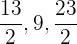

Resumir com IA:


