A matriz inversa é um conceito fundamental em álgebra linear que desempenha um papel crucial em uma variedade de aplicações sistemas de equações lineares até transformações lineares em geometria e programação linear.
Nesta série de exercícios, exploraremos a noção de matriz inversa, como calculá-la e utilizá-la para resolver sistemas de equações lineares
Prepare-se para se aprofundar no fascinante mundo das matrizes inversas e fortalecer suas habilidades em álgebra linear!
Calcule, pelo método de eliminação de Gauss, a matriz inversa de:
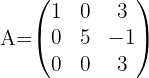
1 Construa uma matriz do tipo 

2 Utilize o método de eliminação de Gauss para transformar a metade esquerda, A, na matriz identidade, e a matriz que resultar no lado direito será a matriz inversa: A−1.
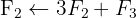





A matriz inversa é:
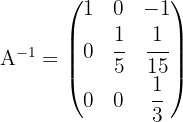
Calcule, pelo método de eliminação de Gauss, a matriz inversa de:
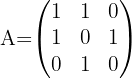
1 Construa uma matriz do tipo 

2 Utilize o método de Gauss para transformar a metade esquerda, A, na matriz identidade, e a matriz que resultar no lado direito será a matriz inversa:A−1.
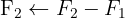


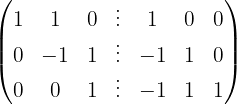
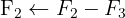



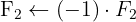

A matriz inversa é:
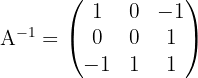
Calcule, pelo método de eliminação de Gauss, a matriz inversa de:

1 Construa uma matriz do tipo 

2 Utilize o método de Gauss para transformar a metade esquerda, A, na matriz identidade, e a matriz que resultar no lado direito será a matriz inversa: A−1.
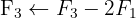






Encontre pelo determinante a matriz inversa de:
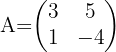
1 Obtemos o determinante:
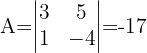
2 Obtemos a matriz adjunta:
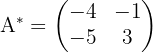
3 Obtemos a matriz trasposta de 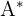
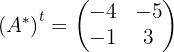
4 Dividimos a transposta da adjunta pelo determinante:


Encontre pelo determinante a matriz inversa de:
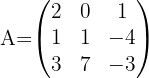
1 Obtemos o determinante:
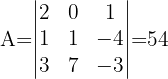
2 Obtemos matriz adjunta:
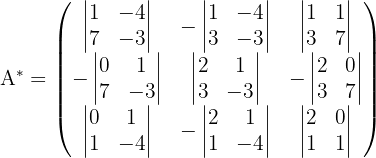
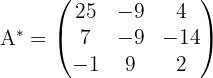
3 Obtemos s a matriz transposta de 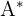

4 Dividimos a transposta da adjunta pelo determinante:

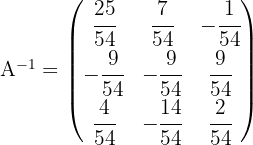
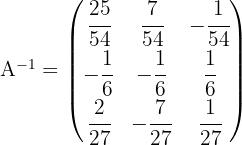
Encontre pelo determinante a matriz inversa de:
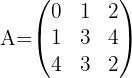
1 Obtemos o determinante:
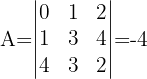
2 Obtemos a matriz adjunta
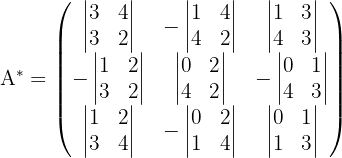

3 Obtemos a matriz transposta de 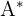
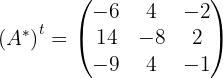
4 Dividimos a transposta da adjunta pelo determinante:


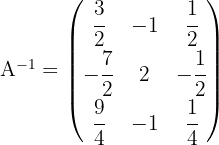
Para quais valores de  a matriz
a matriz 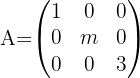 não admite matriz inversa?
não admite matriz inversa?
1 Calculamos o determinante da matriz triangular, que é igual ao produto dos elementos da sua diagonal:
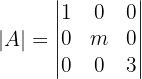

2 Igualamos o determinante a zero e resolvemos a equação:
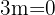

Portanto, a matriz  tem inversa para qualquer valor real
tem inversa para qualquer valor real 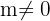
¿Para qué valores de  la matriz
la matriz 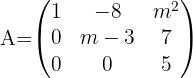 no admite matriz inversa?
no admite matriz inversa?
1 Calculamos la determinante de la matriz triangular superior, la cual es igual al producto de los elementos de su diagonal
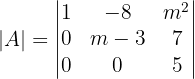
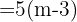
2 Igualamos la determinante a cero y resolvemos la ecuación
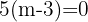
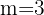
Por lo que la matriz  tiene inversa para cualquier valor real de
tiene inversa para cualquier valor real de 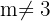
Para quais valores de  la matriz
la matriz 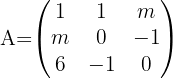 não admite matriz inversa?
não admite matriz inversa?
1 Calculamos o determinante da matriz:

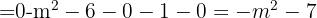
2 Igualamos o determinante a zero e resolvemos a equação:
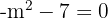
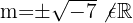
Logo, a matriz  admite matriz inversa para qualquer valor real de
admite matriz inversa para qualquer valor real de 
Para quais valores de  a matriz
a matriz 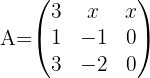 não admite matriz inversa?
não admite matriz inversa?
1 Calculamos o determinante da matriz
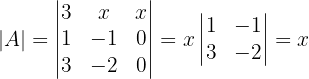
Para  a matriz
a matriz  não possui inversa.
não possui inversa.
Resumir com IA:


