Bem-vindos à nossa página dedicada a exercícios resolvidos sobre gráficos de funções! Se você está interessado em entender como as funções matemáticas podem ser visualizadas e analisadas graficamente, chegou ao lugar certo.
Neste espaço, exploraremos conceitos-chave relacionados à representação gráfica de funções lineares e quadráticas. Ofereceremos uma variedade de exercícios práticos e explicações passo a passo para te ajudar a desenvolver suas habilidades neste campo fascinante.
Nestes exercícios, será necessário traçar ou analisar gráficos de funções para extrair informações fundamentais sobre o comportamento deles, uma combinação que, sem dúvida, fará de você um verdadeiro especialista nesta área. Mergulhe nesses exercícios interessantes! Bora?
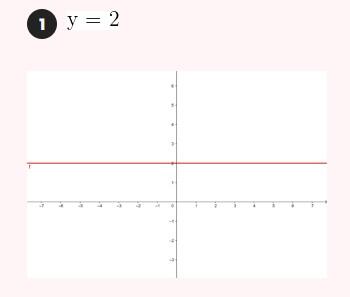
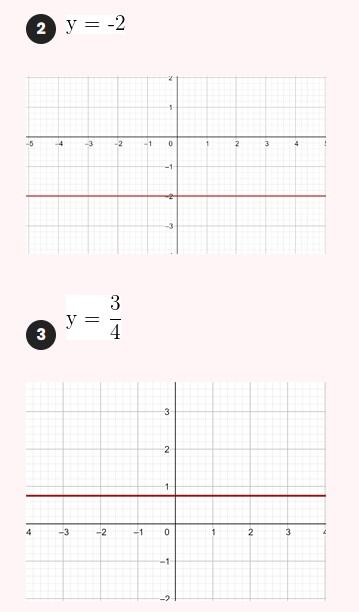
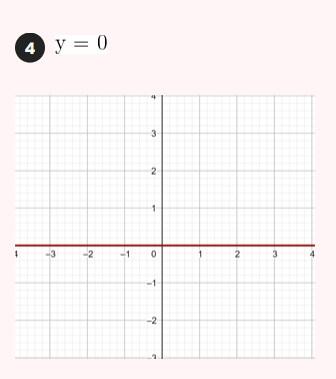
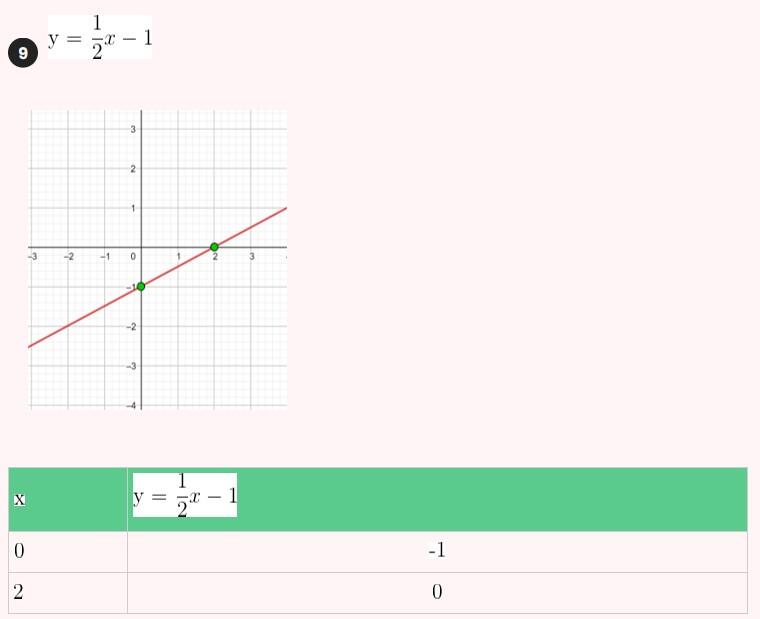
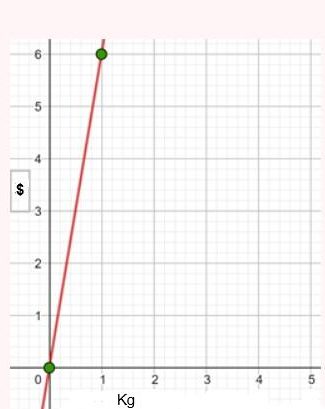
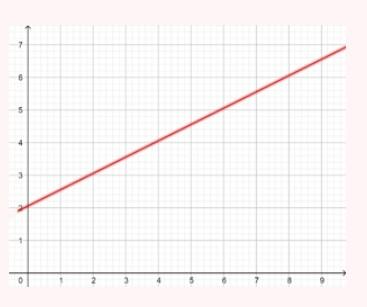
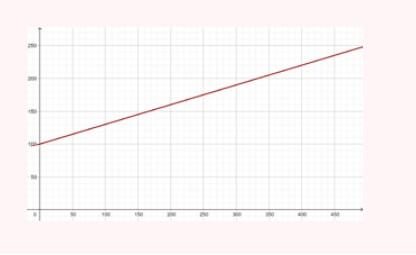
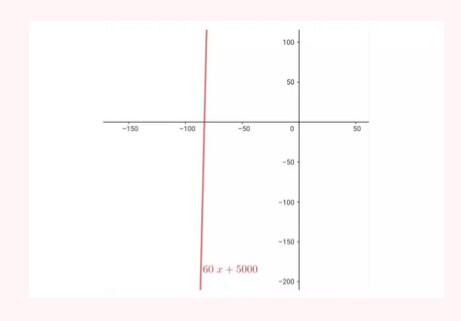
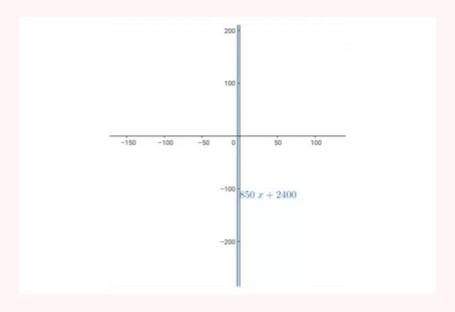
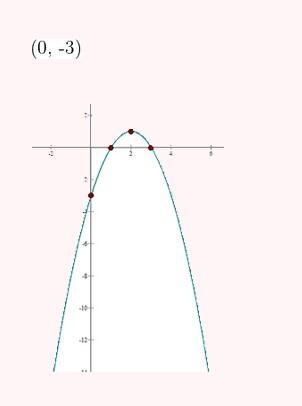
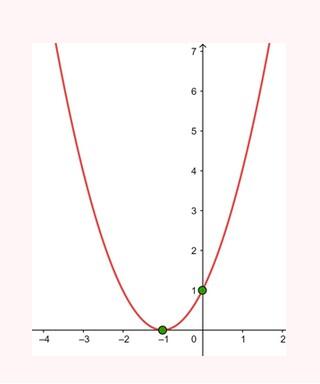
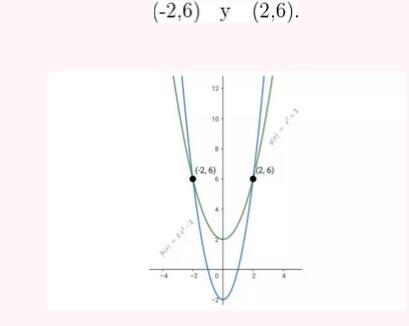
Represente as seguintes retas: Represente as seguintes funções, sabendo que: 1) Tem inclinação -3 e ordenada na origem -1. 1) Tem inclinação -3 e ordenada na origem -1. 2) Tem inclinação 4 e passa pelo ponto (-3, 2). 3) Passa pelos pontos A (-1,5) e B (3, 7). 4) Passa pelo ponto P (2, -3) e é paralela à reta de equação y = -x + 7 Três quilos de biscoito custa R$18. Escreva e represente a função que define o custo dos biscoitos em função dos quilos comprados. 1) A ordenada de origem é 0 que corresponde o valor de 0 quilos. 2) A inclinação é 3) A equação da reta é y = 6x Nas 10 primeiras semanas de cultivo de uma planta, que inicialmente media 2 cm, observou-se que seu crescimento é diretamente proporcional ao tempo, visto que, na primeira semana, ela passou a medir 2,5 cm. Estabeleça uma função que determine a altura da planta em função do tempo e represente graficamente. Altura inicial = 2 cm é a ordenada na origem. Crescimento semanal = 2.5 - 2 = 0.5 é a inclinação. A equação da reta é y = 0.5x + 2 Para alugar um carro é cobrado R$ 100 de diária mais R$ 0,30 por quilômetro rodado. Encontre a equação da reta que relaciona o custo diário com o número de quilômetros e faça sua representação. Se em um dia foram percorridos um total de 300 quilômetros, qual valor deve ser pago? A ordenada na origem é o valor fixo da diária, ou seja, R$ 100. A inclinação é o custo por quilômetro, que é R$ 0,30. A equação da reta que relaciona o custo diário y com o número de quilômetros x percorridos é: y = 0,30x + 100 Agora, se em um dia foram percorridos 300 km, basta substituir x = 300 na equação: y = 0,30 (300) + 100 y = 90 + 100 y = 190 Portanto, o valor a ser pago por percorrer 300 km em um dia é de R$ 190. Um salão de eventos oferece seus serviços em um único pacote para 100 pessoas a um custo de R$ 5000. Além disso, a política do salão estabelece que, se as 100 pessoas forem ultrapassadas, será cobrado R$ 60 por pessoa extra. Escreva e represente a função que define esses custos. Use essa função para calcular o custo de um excedente de 17 pessoas. Sabemos que o pacote tem um custo de R$ 5000, independentemente de serem 100 ou menos pessoas. Portanto, estamos lidando com uma função constante até 100 pessoas: C(x) = 5000, para x ≤ 100 Agora, para cada pessoa excedente, o salão cobra R$ 60 por pessoa extra. Isso significa que, após 100 pessoas, a função deixa de ser constante e se torna uma função linear, cuja inclinação é 60, correspondente ao custo extra por pessoa. Assim, a função, considerando o número de pessoas extras (e = x − 100), é: C(x) = 5000 + 60 (x − 100), para x > 100 Simplificando a função: C(x) = 5000 + 60x − 6000 = 60x − 1000, para x > 100 Cálculo para um excedente de 17 pessoas: Se houver 17 pessoas além do limite de 100, o total de convidados será x = 100 + 17 = 117. Substituímos na função: C(117) = 5000 + 60 (117 − 100) C(117) = 5000 + 60 (17) C(117) = 5000 + 1020 = 6020 Portanto, o custo total para um evento com 117 pessoas (17 pessoas a mais) será de R$ 6020. Uma casa na praia, com capacidade para 20 pessoas, tem um custo por noite de R$ 800. Além disso, exige-se uma reserva mínima de 3 noites, com a opção de alugar a propriedade por mais 2 noites ao custo de R$ 850 cada uma. Escreva e represente a função que modela essa situação. Um grupo de amigos decide alugar a propriedade e deseja estender a estadia por mais 2 noites. Quanto deverão pagar no total? A reserva mínima é de 3 noites, com um custo fixo de R$ 800 por noite. O custo total para as 3 as noites obrigatórias é: C(3) = 800⋅3 = 2400 Isso pode ser representado como uma função constante: C(x) = 2400 , para x = 3 Agora, se o grupo optar por noites extras, cada uma custa R$ 850. Para incorporar esse custo adicional, usamos uma função linear, onde o número de noites extras (e = x − 3) é a variável independente: C(x)= 2400 + 850 (x − 3) , para x > 3 Simplificando: C(x)= 2400 +850x − 2550 = 850x − 150, para x > 3 Para as 2 noites extras, o total de noites será x = 3 + 2 = 5. Substituímos na função: C(5) = 2400 + 850(5−3) C(5) = 2400 + 850(2) C(5) = 2400 + 1700 = 4100 Portanto, o grupo deverá pagar R$ 4100 no total. Encontre o vértice e a equação do eixo de simetria das seguintes parábolas: 1) y= (x-1)²+1 Vértice V = (1, 1) Eixo de Simetria x = 1 2) y = 3(x - 1)² + 1 Vértice V = (1, 1) Eixo de Simetria x = 1 3) y = 2(x + 1)² - 3 Vértice V = (-1, -3) Eixo de Simetria x = -1 4) y = -3 (x - 2)² - 5 Vértice V = (2, -5) Eixo de Simetria x = 2 5) y = x² - 7x - 18 Vértice Eixo de Simetria 6) y = 3x² + 12x - 5 Vértice V = (-2, -17) Eixo de Simetria x = 2 Indique, sem desenhá-las, em quantos pontos as seguintes parábolas cruzam o eixo das abcissas. Dois pontos de encontro Não há pontos de encontro Um ponto de encontro Dois pontos de encontro Represente em gráficos as equações a seguir: 1) Calculamos as coordenadas do vértice Buscamos o ponto de encontro com o eixo OX Buscamos pontos de encontro com o eixo EY 2) Calculamos as coordenadas do vértice Buscamos o ponto de corte com o eixo OY Uma função do 2º grau tem a forma y = x² + ax + a e passa pelo ponto (1, 9). Calcule o valor de a: Substituimos o ponto da função Conhecemos a equação de 2º grau y = ax² + bx + c que passa pelos pontos passa peos pontos (1, 1), (0, 0) . Calcula q, b e c Substituímos o valor de cada ponto na equação: Resolvemos o processo através do sistema de redução A função de 2º grau é: y - x² Considere as equações de 2ª grau: Calcule os pontos de interseções. Para encontrar os pontos de interseção dessas funções, devemos igualar ambas. Assim, temos que: Agora, substituímos esses valores em qualquer uma das funções quadráticas: Portanto, os pontos de interseção das funções quadráticas são: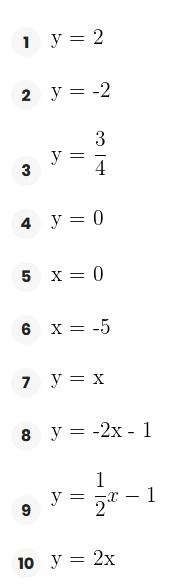
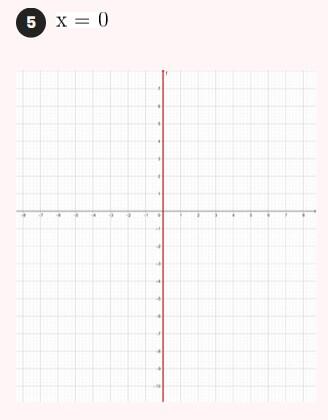
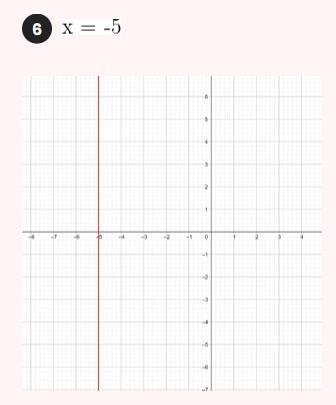
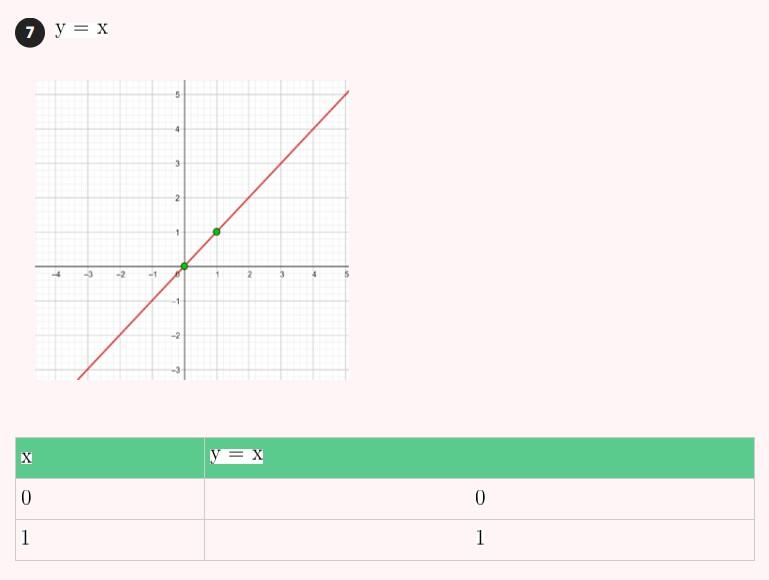
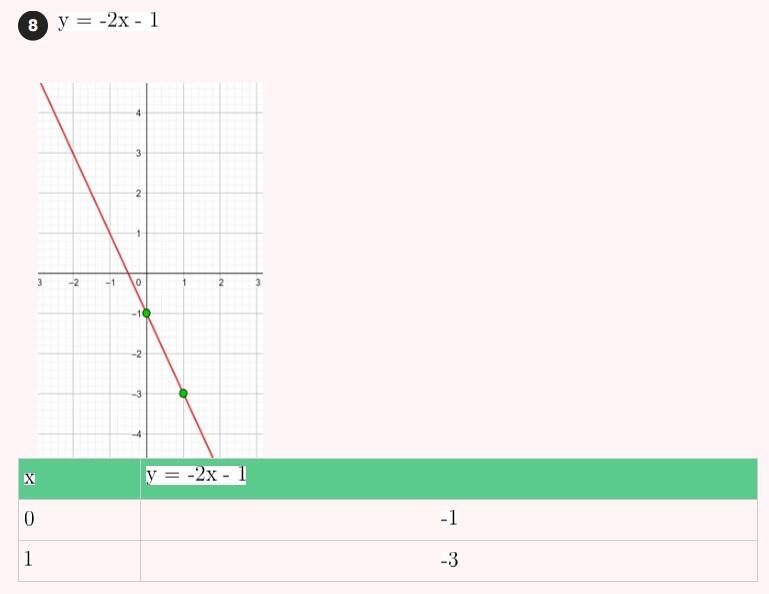
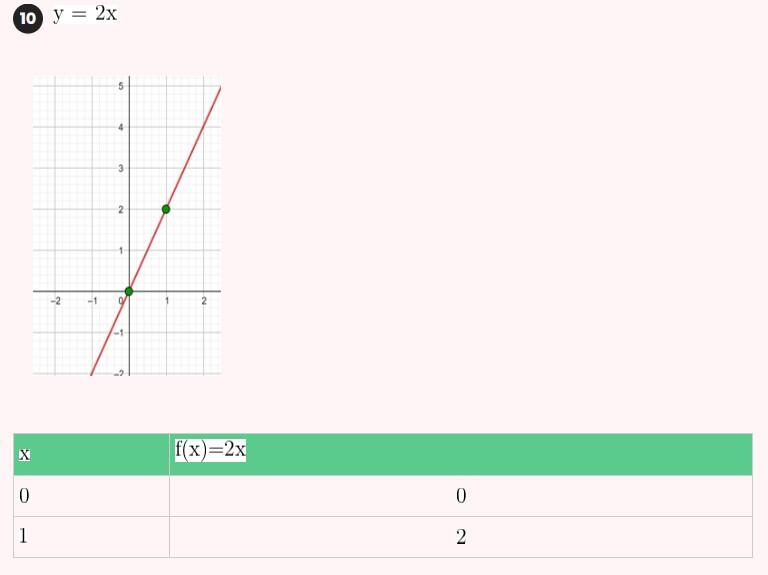
2) Tem inclinação 4 e passa pelo ponto (-3, 2).
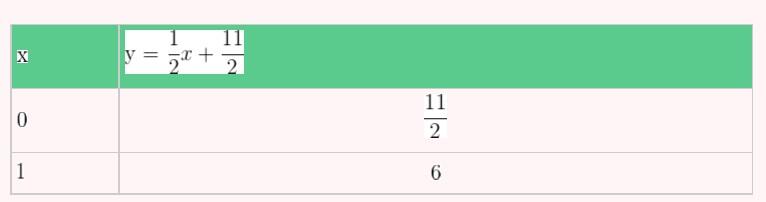
3) Passa pelos pontos A (-1,5) e B (3, 7).
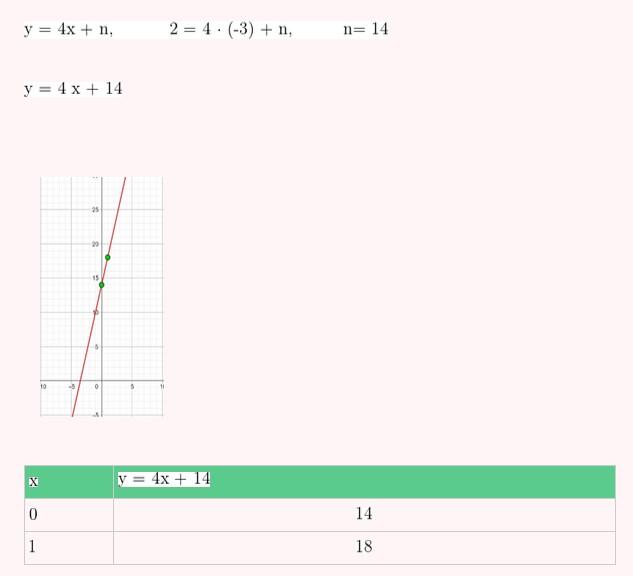
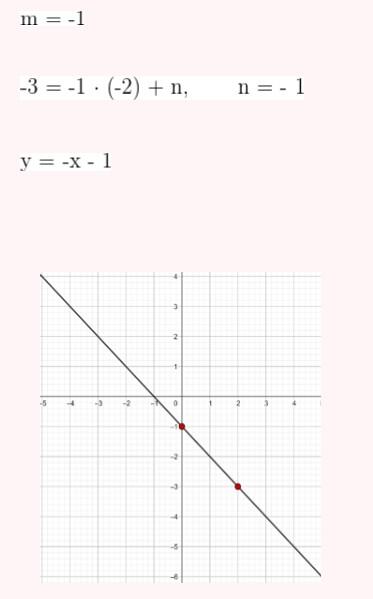
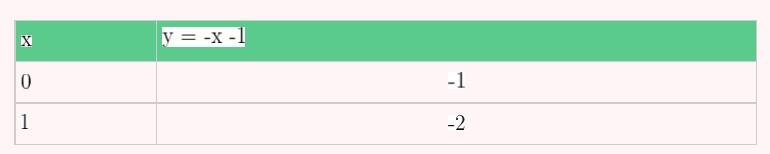
4) Passa pelo ponto P (2, -3) e é paralela à reta de equação y = -x + 7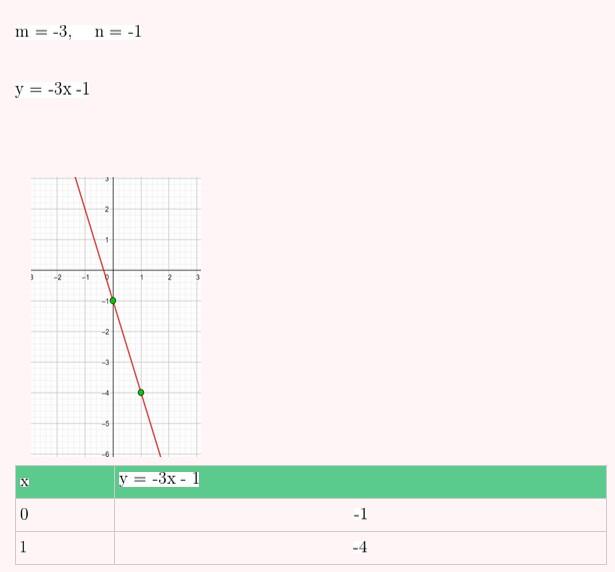
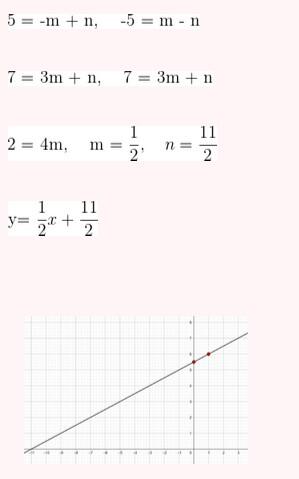
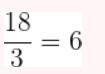
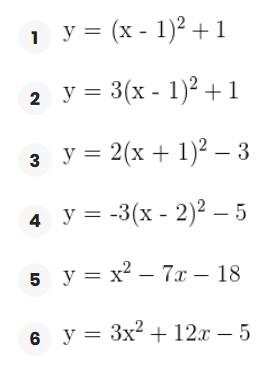
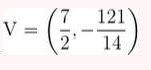
![]()
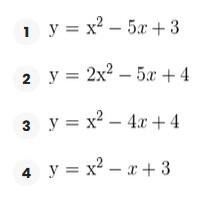
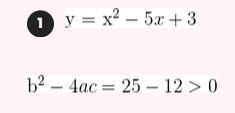
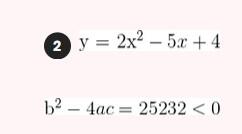
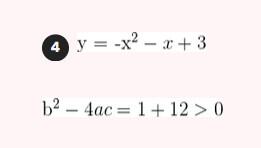
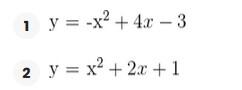
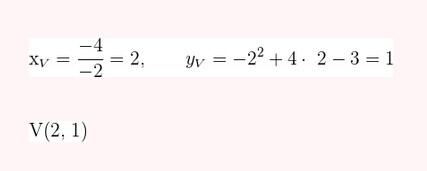
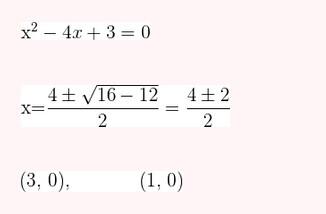
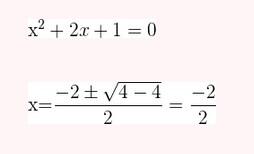
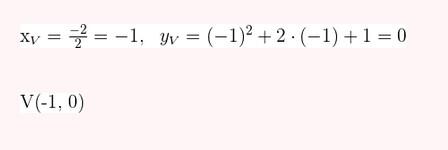
![]()
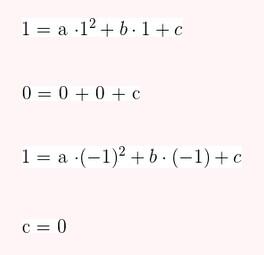
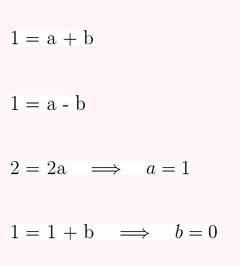
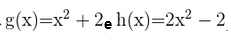 .
.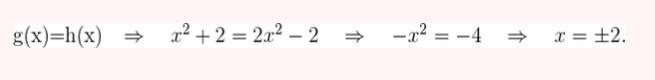

Resumir com IA:


