
Como encontrar a função inversa
Lembre-se de que a função inversa de  é definida como aquela função
é definida como aquela função  tal que
tal que 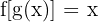 e
e 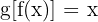 . Portanto, podemos obtê-la a partir de
. Portanto, podemos obtê-la a partir de  .
.
Além disso, a função inversa de  costuma ser denotada como
costuma ser denotada como  (note que o
(note que o  e na expressão anterior não se refere a um expoente negativo, mas apenas indica que é a função inversa).
e na expressão anterior não se refere a um expoente negativo, mas apenas indica que é a função inversa).
Observação: em geral, para que uma função  tenha uma função inversa, é necessário que a função seja um-a-um (ou bijetora). Quando isso não ocorre, é necessário restringir o domínio.
tenha uma função inversa, é necessário que a função seja um-a-um (ou bijetora). Quando isso não ocorre, é necessário restringir o domínio.
Lembre-se de que uma função um-a-um é aquela que atribui a cada elemento do domínio um valor diferente no contradomínio. Ou seja, se 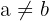 então
então 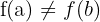 .
.
Método para encontrar a função inversa
1 Substitua  por
por  .
.
2 Isolamos a variável  . Assim, obtemos uma expressão da forma
. Assim, obtemos uma expressão da forma 
3 Em 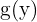 substituímos as
substituímos as  por
por  .
.
4 Finalmente, troque o  do lado esquerdo por
do lado esquerdo por  .
.
Exemplo: Consideremos a função 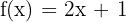 . Vamos seguir o procedimento para encontrar a função inversa:
. Vamos seguir o procedimento para encontrar a função inversa:
1 Substituímos  por
por  :
: 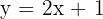 .
.
2 Isolamos  :
:
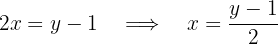
onde 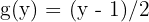
3 Trocamos as  por
por  :
:
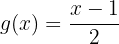
4 Depois, trocamos o  do lado esquerdo por
do lado esquerdo por  :
:
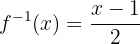
Por fim, verificamos se a função é realmente a inversa:
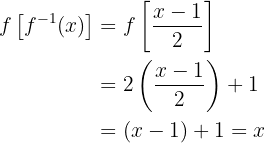
onde podemos observar que satisfaz que  .
.
Exercícios propostos
Encontre a função inversa da seguinte função linear:
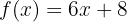
Encontraremos a função sem listar os passos. Temos  , onde substituímos
, onde substituímos  por
por  :
:
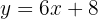
Depois, isolamos  :
:
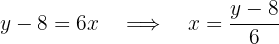
Por fim, substituímos  for
for  e
e  por
por  :
:
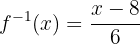
Essa é a função inversa.
Encontre a função inversa da seguinte função:

Primeiro, substituímos  por
por  :
:
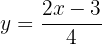
Depois, isolamos  :
:

Ou seja,

Por fim, substituímos  por
por  e
e  por
por  :
:
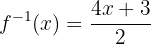
Essa é a função inversa.
Encontre a função inversa da seguinte função (não é necessário simplificar):
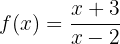
Começamos substituindo  por
por  :
:
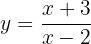
Depois, isolamos  . ara isso, primeiro multiplicamos por
. ara isso, primeiro multiplicamos por  :
:

Em seguida, passamos o  para um lado da equação e os termos restantes para o outro:
para um lado da equação e os termos restantes para o outro:
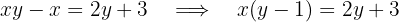
Por último, dividimos por 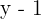 :
:
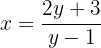
Portanto, a função inversa é:
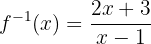
Calcule a função inversa da seguinte função quadrática.
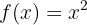
Observe que  não é uma função um-a-um (por exemplo,
não é uma função um-a-um (por exemplo, 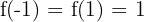 ).Portanto, ela não tem uma função inversa em todo o domínio.
).Portanto, ela não tem uma função inversa em todo o domínio.
No entanto, se considerarmos como domínio o intervalo  , então a função será um-a-um. Nesse caso, a inversa é obtida da seguinte forma:
, então a função será um-a-um. Nesse caso, a inversa é obtida da seguinte forma:

Isolando  (e utilizando o fato de que
(e utilizando o fato de que 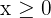 no domínio restrito):
no domínio restrito):
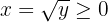
Portanto, neste caso, a função inversa é:
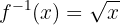
Por outro lado, se restringirmos o domínio para 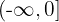 , então a função inversa é obtida da seguinte forma:
, então a função inversa é obtida da seguinte forma:

Em seguida, isolamos  (que satisfaz
(que satisfaz 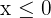 ):
):
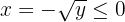
Portanto, a função inversa é:

Isso significa que 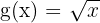 é a inversa de
é a inversa de  apenas quando o domínio é os números reais não negativos
apenas quando o domínio é os números reais não negativos  . Se o domínio for todos os números reais, a função não tem inversa.
. Se o domínio for todos os números reais, a função não tem inversa.
Calcule a função inversa da seguinte função:
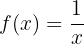
Começamos substituindo  por
por  :
:
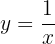
Depois, isolamos:  :
:
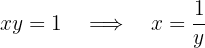
Portanto, a função inversa é:
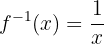
Calcule a função inversa da seguinte função:
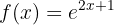
Começamos substituindo  por
por  :
:
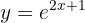
Depois, lembre-se de que o logaritmo natural satisfaz:
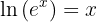
Assim, aplicamos o logaritmo natural em ambos os lados da equação:
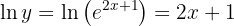
Dessa forma,
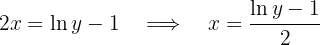
Portanto, a função inversa é:
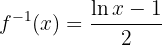
Calcule a função inversa da seguinte função:
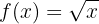
As funções radicais são sim uma-a-uma, portanto, têm função inversa:

Sabemos que  . Depois, elevamos ambos os lados da equação ao quadrado:
. Depois, elevamos ambos os lados da equação ao quadrado:
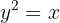
Portanto, a função inversa é:

onde 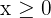 (como fazemos a troca de
(como fazemos a troca de  por
por  , então no final
, então no final  é quem satisfaz
é quem satisfaz 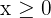 ).
).
Em outras palavras, para que 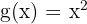 seja a função inversa de
seja a função inversa de  , deve satisfazer que
, deve satisfazer que  e tenha como domínio apenas
e tenha como domínio apenas  .
.
Encontre a função inversa de:

Sabemos que a função de raiz cúbica é uma-a-uma, tem como imagem todos os números reais, e seu contradomínio também são todos os números reais. Portanto, ela terá uma inversa cujo domínio são todos os reais:

Elevamos os dois lados ao cubo:

Ou seja,
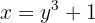
Portanto, a função inversa é:
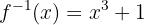
Encontre a função inversa de:

Asimismo, verifica que
a 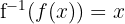
b 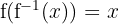
Primeiro, encontramos a função inversa. Para isso, substituímos  por
por  :
:

Depois, isolamos  :
:

Ou seja,
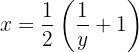
Já temos  isolado. No entanto, simplificamos um pouco:
isolado. No entanto, simplificamos um pouco:
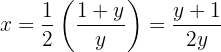
Portanto, a inversa é:

Agora, verificamos o que nos foi pedido:
a) Primeiramente, verificamos que 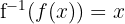 . Para isso, substituímos
. Para isso, substituímos  pelo seu valor:
pelo seu valor:
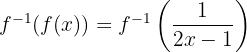
Em seguida, avaliamos  com o argumento dado:
com o argumento dado:
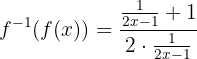
Simplificamos:

Ou seja,
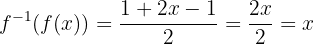
Portanto, a primeira relação é satisfeita.
b) Agora, verificamos que 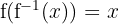 . Primeiro, substituímos
. Primeiro, substituímos  pela expressão:
pela expressão:
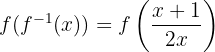
Em seguida, avaliamos  :
:
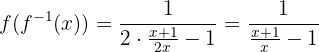
Ou seja,
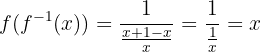
Portanto, a segunda relação também é satisfeita.
Encontre a função inversa de:
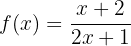
y verifica que 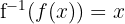 .
.
Começamos calculando a inversa, substituindo  por
por  :
:
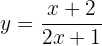
Depois, isolamos  . Para isso, multiplicamos por
. Para isso, multiplicamos por  :
:

Em seguida, passamos os termos com  para o lado esquerdo da equação, e os termos restantes para o lado direito:
para o lado esquerdo da equação, e os termos restantes para o lado direito:
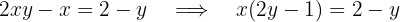
Portanto,
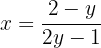
Ou seja, a função inversa é:
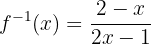
Agora, verificamos se satisfaz que 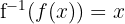 . Primeiro, substituímos a expressão de
. Primeiro, substituímos a expressão de  :
:

Agora, avaliamos a inversa:
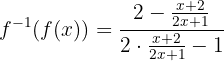
Simplificamos:
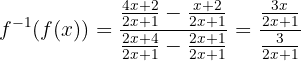
Logo:

Portanto, a relação é válida.
Calcule a inversa da função:
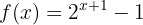
Começamos substituindo 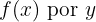 , depois isolamos
, depois isolamos  :
:
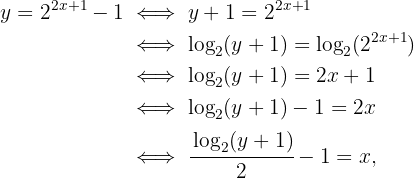
Ou seja,
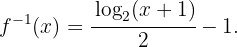
Calcule a inversa da função 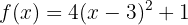 no domínio apropriado.
no domínio apropriado.
Primeiro, podemos observar que não se trata de uma função injetora. De fato, 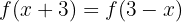 . Então, buscamos a inversa no intervalo
. Então, buscamos a inversa no intervalo  . Começamos substituindo
. Começamos substituindo 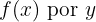 , depois isolamos
, depois isolamos  :
:
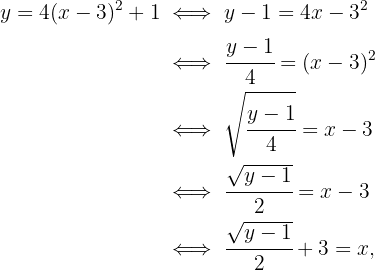
Ou seja,
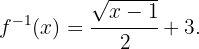
Calcule a inversa da função:
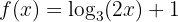
Começamos substituindo 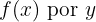 , depois isolamos
, depois isolamos  :
:
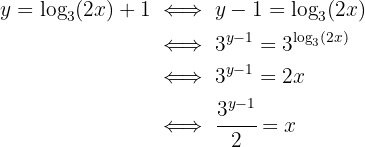
Ou seja,
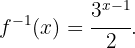
Calcule a inversa da função:
Começamos substituindo 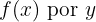 , depois isolamos
, depois isolamos  :
:
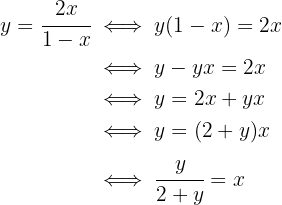
Ou seja,
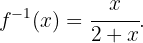
Calcule a inversa da função:
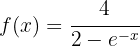
Começamos substituindo 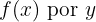 , depois isolamos
, depois isolamos  :
:
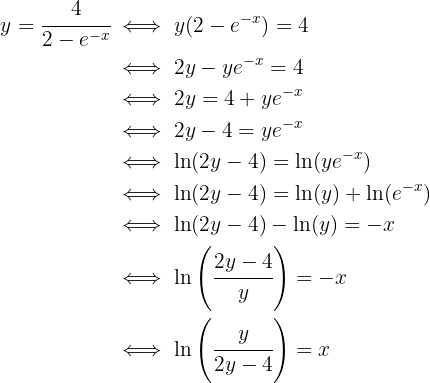
Ou seja,
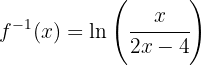
Resumir com IA:












