Temas

Exercícios sobre gráficos e domínios de funções definidas por partes
Para as seguintes funções, desenhe o gráfico e determine seu domínio e imagem.
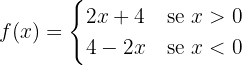
Observamos que, no intervalo 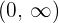 , ou seja, do lado direito do plano temos a função
, ou seja, do lado direito do plano temos a função 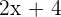 .
.
Por outro lado, no intervalo  , lado esquerdo do plano temos a função
, lado esquerdo do plano temos a função 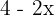 .
.
Portanto, o gráfico é como mostrado na figura a seguir:
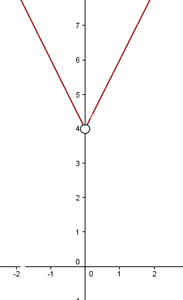
Como mencionamos anteriormente, a função está definida para 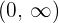 e para
e para  . Assim, o domínio é
. Assim, o domínio é
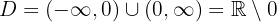
Por outro lado, a partir do gráfico, podemos ver que a imagem (ou conjunto dos valores assumidos pela função) é

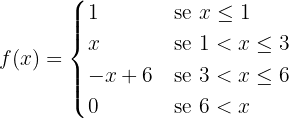
Observamos que a função está definida em quatro regiões distintas. Primeiro, no intervalo 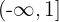 , ela assume o valor 1. Em seguida, no intervalo
, ela assume o valor 1. Em seguida, no intervalo 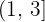 , assume o valor
, assume o valor  e, assim, sucessivamente.
e, assim, sucessivamente.
Portanto, o gráfico é como mostrado na figura a seguir:
Em seguida, observamos que o domínio é:
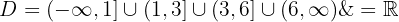
Por outro lado, observamos que a imagem (ou conjunto dos valores assumidos pela função) é:
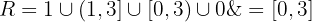

Se representarmos graficamente as expressões correspondentes a cada uma das regiões dadas, obtemos o seguinte gráfico:
Além disso, o domínio é dado por:
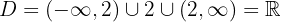
Em seguida, o conjunto imagem (ou conjunto dos valores assumidos pela função) é dado por
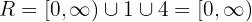
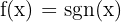
Vamos lembrar que 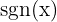 é a função sinal, definida da seguinte forma:
é a função sinal, definida da seguinte forma:
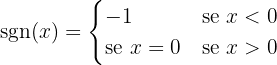
Portanto, o gráfico é dado pela figura a seguir:
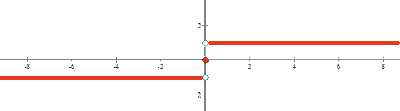
Além disso, o domínio é:
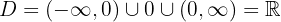
Enquanto isso, o conjunto imagem (ou contradomínio) é:

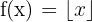
Vamos lembrar que a função 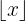 é conhecida como função piso e é definida como o maior inteiro
é conhecida como função piso e é definida como o maior inteiro  tal que
tal que 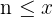 . Por exemplo:
. Por exemplo:
1 
2 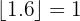
3 
4 
Assim, o gráfico é mostrado na figura a seguir:
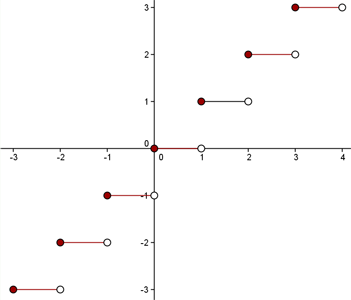
Observamos que o domínio da função é:

Enquanto o conjunto imagem é:


Nesse caso, para cada  estamos subtraindo
estamos subtraindo 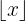 , que corresponde à parte inteira. Portanto, o valor de
, que corresponde à parte inteira. Portanto, o valor de  é a parte decimal de
é a parte decimal de  .
.
Assim, o gráfico é o seguinte:
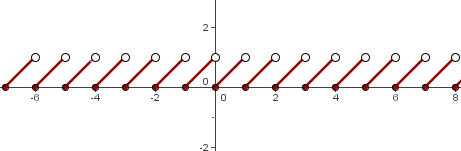
Esse gráfico é conhecido como “dente de serra”.
Além disso, observamos que vale a relação.
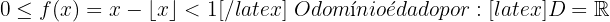
O conjunto imagem é dado por
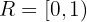

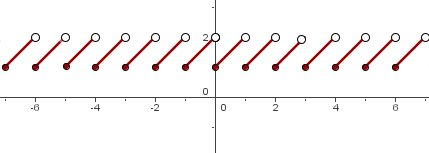
Vamos notar que essa função é exatamente a mesma que a anterior, mas com a soma de 1. Portanto, o gráfico é o seguinte:
O domínio é o mesmo,  , enquanto o conjunto imagem é:
, enquanto o conjunto imagem é:

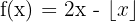
Podemos ver essa função como 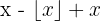 . Portanto, à função da parte decimal de
. Portanto, à função da parte decimal de  somamos
somamos  . O gráfico dessa função é o seguinte:
. O gráfico dessa função é o seguinte:
Em seguida, o domínio também é  , enquanto o conjunto imagem agora é
, enquanto o conjunto imagem agora é  , o que pode ser observado no gráfico.
, o que pode ser observado no gráfico.

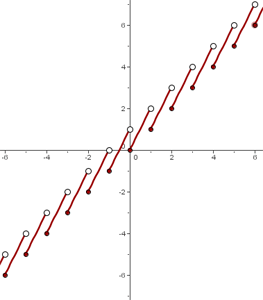
Vamos observar que, agora, primeiro dividimos por 2 e, em seguida, obtemos a parte inteira. Portanto, trata-se de uma espécie de “escalonamento” da função piso. É como se estivéssemos esticando o gráfico horizontalmente.
O gráfico é mostrado na figura a seguir.
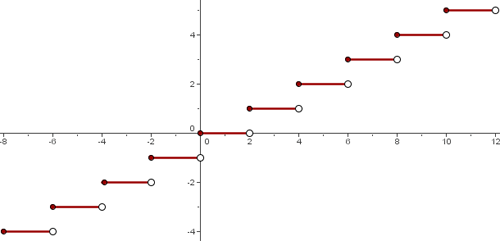
No entanto, o domínio e o conjunto imagem são os mesmos da função piso:

e

Determinação da função a partir do gráfico
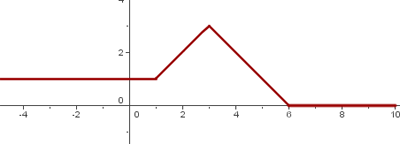
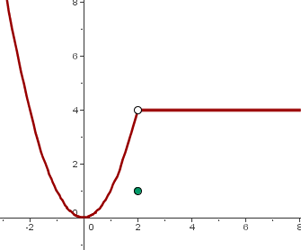
Observe o gráfico a seguir e determine a expressão analítica da função que ele descreve.
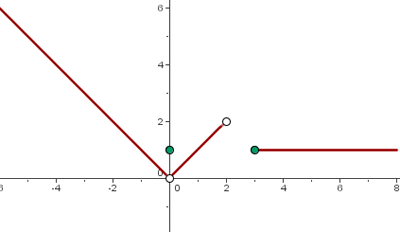
A função  será uma função definida por partes. As funções
será uma função definida por partes. As funções 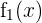 ,
, 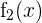 etc. serão funções auxiliares, definidas em partes do domínio.
etc. serão funções auxiliares, definidas em partes do domínio.
1 Primeiro, observe que no intervalo  temos uma reta com inclinação negativa. Na verdade, trata-se da função:
temos uma reta com inclinação negativa. Na verdade, trata-se da função:
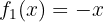
2 Além disso: 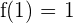 .
.
3 Em seguida, no intervalo  temos a função:
temos a função:  .
.
4 A função não está definida no intervalo: 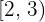 .
.
5 Por fim, no intervalo 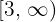 a função é constante:
a função é constante:
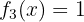
Portanto, a função é dada por:
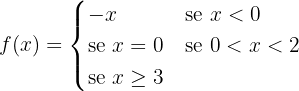
Resumir com IA:












