Neste artigo, exploraremos uma série de exercícios resolvidos que demonstram como trabalhar com funções lineares. Vamos abordar diferentes aspectos, como a identificação da inclinação e da interseção, a representação gráfica e a resolução de problemas práticos.
Sendo assim, represente as funções indicadas e resolva os seguintes problemas.
Exercícios de função linear
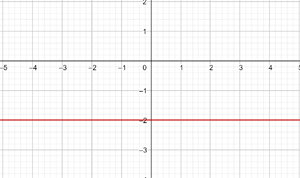
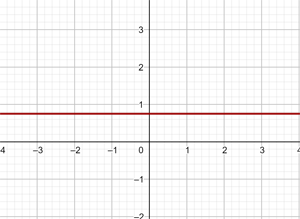
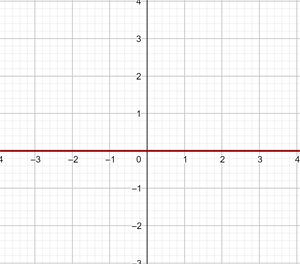
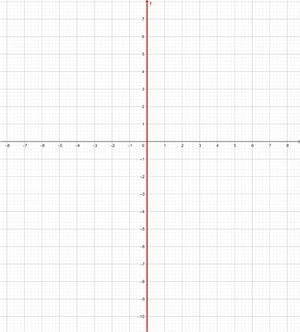
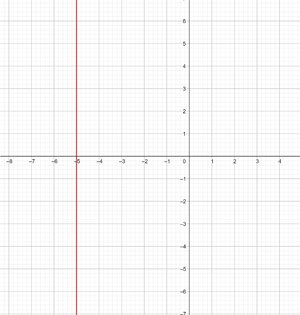
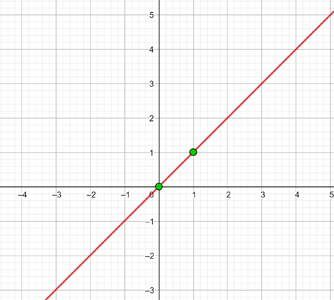
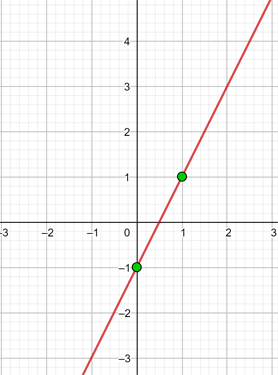
y = 2 Represente a função constante: y = 2 Essa função refere-se a todos os pontos de coordenadas (x,y) onde y = 2, ou seja, todos os pontos (x,2), onde x é uma variável independente, à qual pode ser atribuído qualquer valor. Por exemplo: (1, 2), (−4, 2), (5, 2), e assim por diante. y = - 2 Represente a função constante: y = - 2 Essa função refere-se a todos os pontos de coordenadas (x,y) onde y = - 2, ou seja, todos os pontos (x, -2), onde x é uma variável independente, à qual pode ser atribuído qualquer valor. Por exemplo: (1, -2), (−4, -2), (5, -2), etc. Represente a função constante: Essa função refere-se a todos os pontos de coordenadas (x,y) onde y = 0 Represente a função constante: y = 0 Essa função refere-se a todos os pontos de coordenadas (x,y) onde y = 0, ou seja, todos os pontos (x,0), sendo que x é uma variável independente, que pode ser atribuída qualquer valor. Por exemplo: (1,0), (−4,0), (5, 0), etc. x = 0 Represente a reta vertical: x = 0 Esta não é uma função e refere-se a todos os pontos de coordenadas (x,y) em que x = 0, ou seja, todos os pontos (0,y), sendo que y é uma variável independente, que se pode atribuir qualquer valor. Por exemplo: (0,1), (0,−3), (0,5), e assim por diante. x = - 5 Represente a reta vertical: x = − 5 Esta não é uma função e refere-se a todos os pontos de coordenadas (x,y) onde x = − 5, ou seja, todos os pontos (−5, y), sendo que y é uma variável independente, que pode atribuir qualquer valor. Por exemplo: (−5, 1), (−5, −3), (−5, 5), etc. y = x Represente a função: y = x Essa função refere-se a todos os pontos de coordenadas (x,y) onde y = x, ou seja, todos os pontos (x,y), onde y é igual a x, e ambos são variáveis independentes, podendo ser atribuídos quaisquer valores. Por exemplo: (1, 1), (−3 ,−3), (5, 5), etc. Para poder representar no gráfico de forma correta eficiente, elaboramos uma tabela onde colocamos, à esquerda, os valores de x (quaisquer que escolhermos) e, à direita, o valor correspondente de y, que é calculado pela função. y = 2x Represente a função linear: y = 2x Para facilitar a representação gráfica, elaboramos uma tabela onde, à esquerda, colocamos os valores de x (que podemos escolher livremente) e, à direita, o valor correspondente de y, que será obtido ao calcular o valor de x na função y = 2x. Isso nos ajuda a visualizar de forma mais clara a relação entre os valores de x e y. y = 2x - 1 Represente a função afim: y = 2x − 1 Para facilitar a representação gráfica, criamos uma tabela onde, à esquerda, colocamos os valores de x (que podemos escolher livremente) e, à direita, o valor correspondente de y, obtido ao calcular a expressão y= 2x − 1 com os valores atribuídos a x. Dessa forma, podemos visualizar de maneira mais clara a relação entre x e y nessa função. y = −2x − 1 Represente a função afim: y = - 2x − 1 Para facilitar a representação gráfica, criamos uma tabela onde, à esquerda, colocamos os valores de x (que podemos escolher livremente) e, à direita, o valor correspondente de y, obtido ao calcular a expressão y = -2x − 1 com os valores atribuídos a x. Dessa forma, podemos visualizar de maneira mais clara a relação entre x e y nessa função. Represente a função afim: Para facilitar a representação gráfica, elaboramos uma tabela onde, à esquerda, colocamos os valores de x (que podemos escolher livremente) e, à direita, o valor correspondente de y, obtido ao calcular o valor de y na função com os valores atribuídos a x. Essa abordagem ajuda a visualizar com clareza a relação entre x e y na função. Represente a função afim: Para facilitar a construção do gráfico, elaboramos uma tabela onde, na coluna da esquerda, colocamos os valores de x (que podemos escolher livremente), e, na coluna da direita, registramos os valores correspondentes de y, calculados substituindo x na expressão da função. Essa abordagem torna mais clara a relação entre x e y, ajudando a visualizar o comportamento da função. Represente a seguinte função, sabendo que sua inclinação (coeficiente angular) é −3 e sua interseção com o eixo y (coeficiente linear) é −1 A função afim correspondente é: y = − 3x −1 Represente a seguinte função, sabendo que sua inclinação é 4 e que ela passa pelo ponto (−3,2) A função é: y = mx + n Com m=4, substituímos o valor de m: y = 4x + n Um ponto é (−3,2), substituímos o valor do ponto: 2 = 4 · (−3) + n ⟹ n = 14 Logo, a função é: y = 4 x + 14 Represente a função, sabendo que passa pelos pontos A(−1, 5) e B(3, 7) A função é: y = mx + n Passa pelo ponto (−1,5): 5 = − m + n Passa pelo ponto (3,7): 7 = 3m + n Resolvemos o sistema por redução: −5 = m − n A função é: Represente a seguinte função, sabendo que ela passa pelo ponto P(2,−3) e é paralela à reta de equação y = −x + 7 A função é: y = mx + n Duas retas paralelas têm o mesmo coeficiente angular, logo m = −1 Passa pelo ponto (2,−3): −3 = −1⋅2 + n ⟹ n = −1 Portanto, a função é: Nas primeiras 10 semanas de cultivo de uma planta, que inicialmente media 2 cm, foi observado que seu crescimento é diretamente proporcional ao tempo, passando a medir 2,5 cm na primeira semana. Determine uma função afim que represente a altura da planta em função do tempo e faça a representação gráfica. Altura inicial = 2 cm Crescimento semanal = 2,5 − 2= 0,5 A função é: y = 0,5x + 2 Para o aluguel de um carro, cobra-se um valor fixo de R$ 100 por dia, mais $ 0,30 por quilômetro rodado. Determine a equação da reta que relaciona o custo diário ao número de quilômetros percorridos e elabore o gráfico. Se em um dia foram percorridos 300 km, qual será o valor total a ser pago? A equação da reta que representa o custo é: y = 0,3x + 100 Para calcular o custo com 300 km: y = 0.3 x + 100 y = 0.3 · 300 + 100 y = 190 O valor total a ser pago será de R$190. Calcule os coeficientes da função: f(x) = ax + b, dado que f(0) = 3 e f(1) = 4 Sabemos que: f(0) = 3 ⟹ a⋅0 + b = 3 ⟹ b = 3 Portanto, a função é: Calcule os coeficientes da função: f(x) = ax + b, dado que f(0) = −1 e f(1) = 2. f(0) = −1 ⟹ a⋅0 + b = −1 ⟹ b = −1 Portanto, a função é: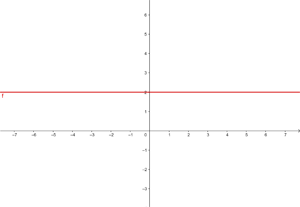
, ou seja, todos os pontos 
) sendo que x é uma variável independente, que pode ser atribuída qualquer valor. Por exemplo: 
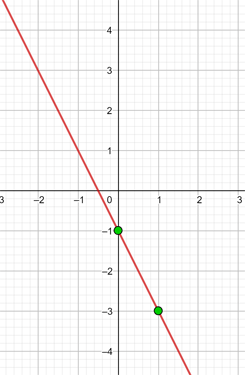
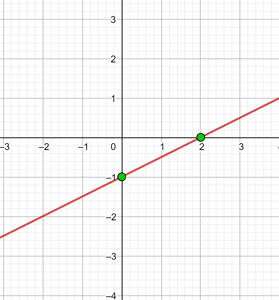
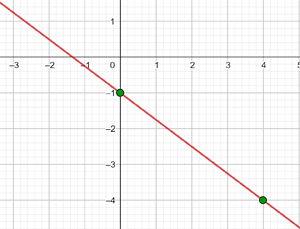
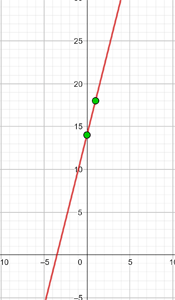
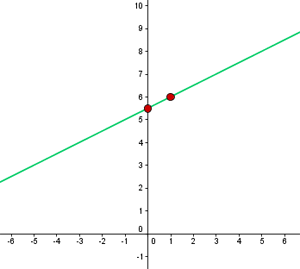
y = − x−1
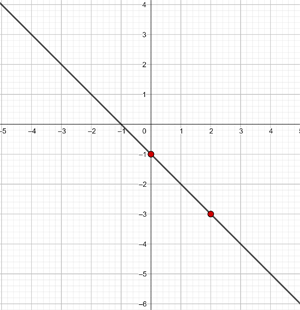
f(1) = 4 ⟹ a⋅1 + b = 4 ⟹ a +3=4 ⟹ a = 1
f(x) = x + 3
f(1) = 2 ⟹ a⋅1 + b = 2 ⟹ a−1 = 2 ⟹ a = 3
f(x) = 3x − 1
Gostou desse artigo? Deixe uma nota!
Loading...
