A Análise Combinatória é um ramo da Matemática que estuda técnicas de contagem, organização e análise das diferentes maneiras pelas quais os elementos podem ser agrupados ou ordenados. Esse conteúdo está presente em diversas situações do cotidiano e possui aplicações importantes em áreas como informática, estatística, biologia e teoria dos jogos.
Nesta coleção de exercícios e problemas de Análise Combinatória, você irá trabalhar conceitos fundamentais como permutações, combinações, arranjos e conjuntos, desenvolvendo o raciocínio lógico e a capacidade de resolver problemas de forma estruturada. Cada atividade foi pensada para reforçar a compreensão dos conceitos e estimular o pensamento analítico.
O material é indicado tanto para quem está iniciando os estudos em Análise Combinatória quanto para quem deseja aprofundar e consolidar o conteúdo. Os exercícios evoluem dos conceitos básicos para desafios mais elaborados, incentivando a identificação de padrões, a escolha de estratégias adequadas e a construção de soluções criativas.
 .
.

Isolamos a incógnita:



Agrupamos os termos semelhantes e os independentes e somamos:



Retiramos os parênteses: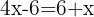
Agrupamos os termos e somamos:

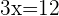
Isolamos a incógnita:
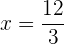
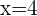


Retiramos os denominadores, para isso, em primeiro lugar, encontramos o mínimo múltiplo comum.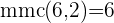
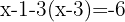
Retiramos os parênteses, agrupamos e somamos os termos semelhantes:
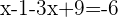
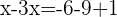
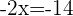
Isolamos a incógnita:
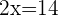
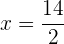

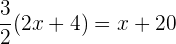
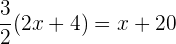
Retiramos parênteses e simplificamos
Retiramos os denominadores, agrupamos e somamos os termos semelhantes
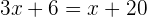
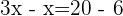
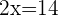

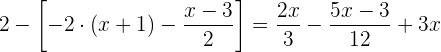
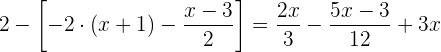
Retiramos o colchete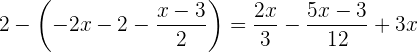
Retiramos os parênteses
Retiramos os denominadores
Retiramos os parênteses
Agrupamos os termos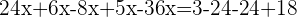
Somamos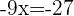
Dividimos os dois membros por 
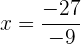



Retiramos os parênteses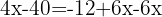
Agrupamos os termos com a variável x de um lado da equação e os independentes do outro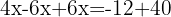
Somamos os termos semelhantes para simplificar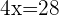
Dividimos a equação entre 




Retiramos os parênteses
Agrupamos os termos com a variável x de um lado da equação e os independentes do outro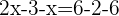
Somamos os termos semelhantes para simplificar
Dividimos entre 




Procuramos o mmc dos denominadores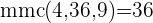
Multiplicamos a equação por 
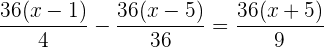
Simplificamos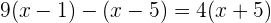
Retiramos os parênteses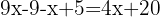
Agrupamos os termos com a variável  de um lado da equação e os independentes do outro
de um lado da equação e os independentes do outro
Somamos os termos semelhantes para simplificar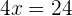
Dividimos entre 
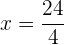
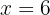


Retiramos os parênteses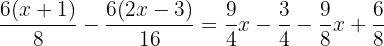
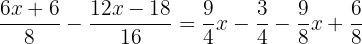
Procuramos o mmc dos denominadores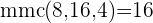
Multiplicamos a equação por 

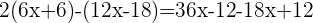
Retiramos os parênteses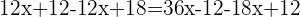
agrupamos os termos semelhantes e somamos

Dividimos entre  toda a equação e isolamos
toda a equação e isolamos 

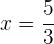
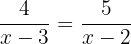
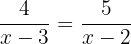
Multiplicamos toda a equação pelo produto dos denominadores, isto é, por 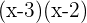

Simplificamos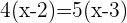
Retiramos os parênteses
Agrupamos os termos semelhantes e somamos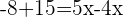

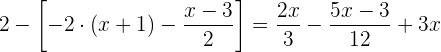
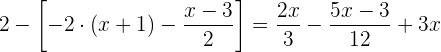
Retiramos os parênteses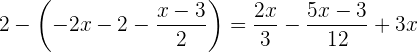

Encontramos o mmc dos denominadores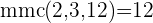
Multiplicamos a equação por 
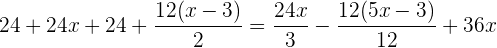

Retiramos os parênteses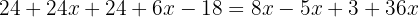
Agrupamos os termos semelhantes e somamos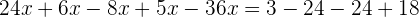

Isolamos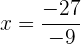

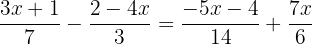
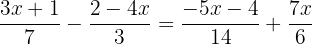
Encontramos o mmc dos denominadores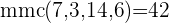
Multiplicamos por 
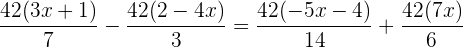
Simplificamos calculando quanto é  entre o respectivo denominador para obter o coeficiente, por exemplo
entre o respectivo denominador para obter o coeficiente, por exemplo
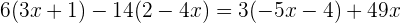
Retiramos os parênteses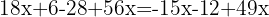
Agrupamos os termos semelhantes e somamos
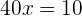
Dividimos entre  e isolamos
e isolamos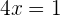
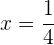
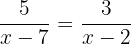
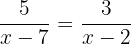
Multiplicamos toda a equação pelo produto dos denominadores, isto é, por 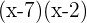

Simplificamos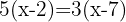
Retiramos os parênteses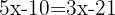
Agrupamos os termos semelhantes e somamos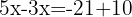
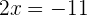
Isolamos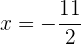
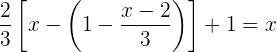
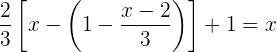
Retiramos os parênteses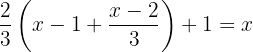
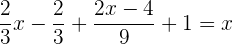
Calculamos o mmc dos denominadores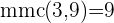
Multiplicamos a equação por 
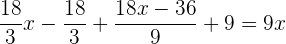
Simplificamos
Agrupamos os termos semelhantes e multiplicamos por 


Resumir com IA:


