Temas
Encontrar os pontos
Considerando a parábola 
, encontre os pontos nos quais a reta tangente é paralela à bissetriz do primeiro quadrante. Encontre a equação da reta tangente e normal nesses pontos.
1. Encontrar os pontos
A bissetriz do primeiro quadrante tem a equação 
, portanto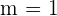 
.
Derivamos a equação da parábola, pois sabemos que a derivada nos indica a inclinação:
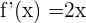
Igualamos a 
e resolvemos para encontrar o valor de x onde isso ocorre:
Avaliamos a função original neste ponto 
:
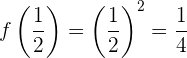
Então,
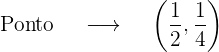
2. Reta tangente
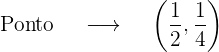
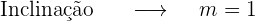
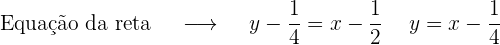
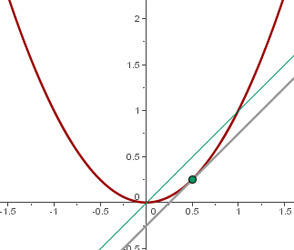
3. Reta normal
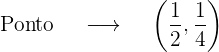
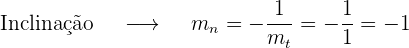
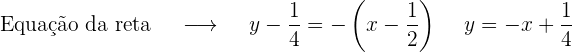
Dada a curva da equação 
, encontre as coordenadas dos pontos da referida curva nos quais a tangente forma com o eixo 
um ângulo de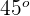 
.
A primeira coisa que devemos saber é que a inclinação de uma reta é igual à tangente do ângulo que ela forma com o eixo.
Ou seja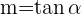 
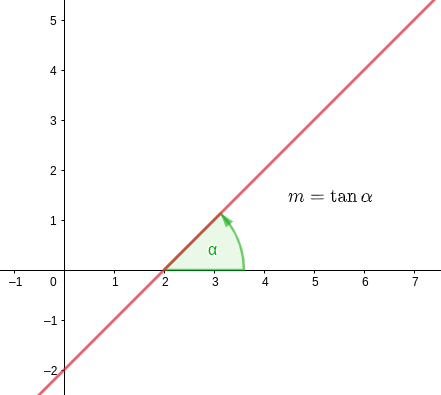
A derivada de 
nos aponta a inclinação da reta tangente.
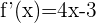
Como quero que a reta tangente forme 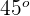com o eixo , estou solicitando que a inclinação tenha o valor de 
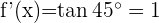
Assim,
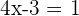
Resolvemos x
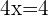
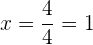
Ao obter o valor de x, conseguimos a abscissa. Para obter o valor da ordenada, avaliamos o ponto 
em sua função original:
Finalmente,
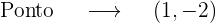
Calcule os pontos nos quais a tangente à curva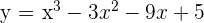 
é paralela ao eixo .
As retas paralelas têm a mesma inclinação. O eixo tem uma inclinação de zero. Sendo assim, eu quero que a tangente à curva tenha uma inclinação de zero. Portanto, eu quero que
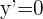
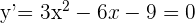
Simplificando, obtemos a equação
Resolvemos, e avaliamos as soluções da função de 
Finalmente, os pontos nos quais a tangente a uma curva é paralela ao eixo são:
Foi desenhada uma reta tangente a uma curva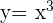 
, cuja inclinação é 
e passa pelo ponto 
. Encontre o ponto de tangência.
A derivada nos fornece a inclinação da reta tangente à curva.
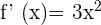
O problema informa que esta inclinação é , então
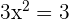
Resolvemos a conta:
Obtemos a equação da reta tangente nestes pontos.
1 Abscissa x=1
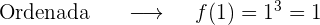
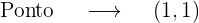
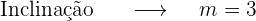
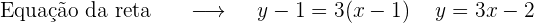
2 Abscissa x=-1
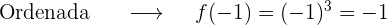
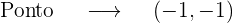
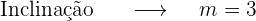
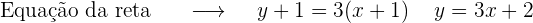
Mas o ponto 
só pertence a reta 
.
Portanto, o ponto de tangencia será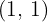 
.
Busque os pontos da curva 
, para que a tangente forme um ângulo de 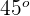com .
1. Obter abscissas
Vale lembrar que a inclinação de uma reta é igual à tangente do ângulo que ela forma com o eixo
Ou seja,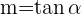
A derivada de nos indica a inclinação da reta tangente
Como quero que a reta tangente forme 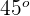con o eixo , estou pedindo que a inclinação tenha o valor de
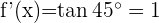
Dessa forma,
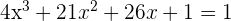
Resolvemos a equação:
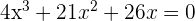
Fazemos a fatoração de x:
Um resultado é:
As outras soluções são obtidas quando:
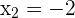
2. Obter ordenadas
Avaliamos os pontos na função original
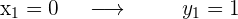
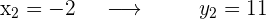
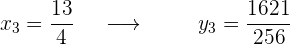
Finalmente,
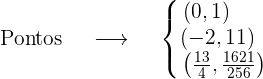
Em que ponto da curva 
, a tangente é paralela à corda que une os pontos (1, 0) e (e, 1)?
A inclinação da corda deve ser igual à derivada da função.
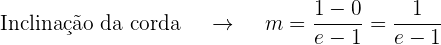
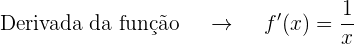
Então,
Avaliamos este ponto em para obter a ordenada
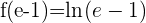
Finalmente:
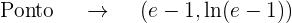
Calcular a equação da reta
Calcule a equação da reta tangente e da normal à curva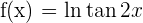 
no ponto de abscissa: 
.
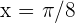1. Reta tangente
Obter inclinação
Fazemos a derivada da função, pois sabemos que a derivada nos indica a inclinação da reta tangente.
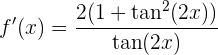
Chegamos ao resultado: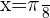 
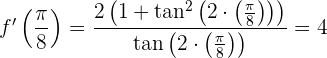
Obter as coordenadas do ponto de tangência
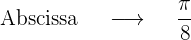
Chegamos à conclusão que a função original neste ponto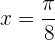 
para obter a ordenada
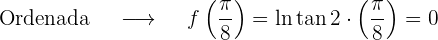
Obter a equação da reta tangente
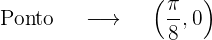
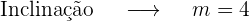
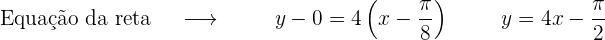
2. Reta normal
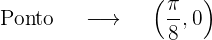
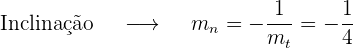
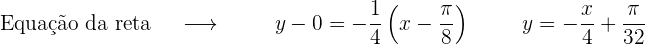
Considerando a equação 
, encontre a equação da reta tangente que seja paralela à reta com a equação 
.
A equação , ao ser resolvido pode ser reescrita desta forma:
Fazendo a derivada que está implícita na equação, temos:
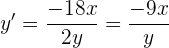
E como a derivada nos fornece a inclinação da reta tangente, a igualaremos a 3, pois é o valor que determinamos. Assim:
Então, temos a operação de equações 2x2.
Resolvemos, substituindo a segunda equação na primeira.
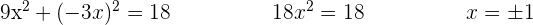
Para obter a ordenada dos pontos basta substituir o valor de 
na equação na equação mais simples da operação
E, assim, obtemos a equação da reta nestes pontos.
1 x=1
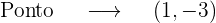
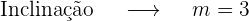
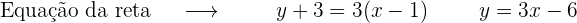
2 x=-1
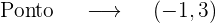
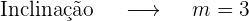
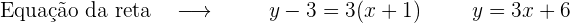
Determinar os parâmetros
Determine os valores do parâmetro b, para que as tangentes da curva da função 
nos pontos de abscissas 
, 
fiquem paralelas.
A derivada de é
Para que fiquem paralelas é necessário entender que as derivadas em e sejam iguais. Ou seja
Assim
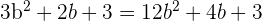
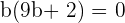
Um resultado é
O outro
Encontre os quoeficientes da equação 
, sabendo que seu gráfico passa por 
e por 
, e nesse último ponto sua tangente tem de inclinação .
Vamos ter 
equações ao substituir o valor da abscissa em e quando igualar ao valor da ordenada dos pontos que passam pelo gráfico
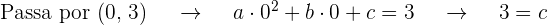
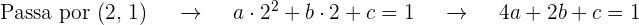
Além do mais, a inclinação da tangente é dada por
Se a inclinação no ponto é 3, isso significa que
Resolvendo a operação de 3x3 se obtém:
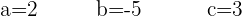
E a equação fica assim
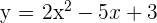
O gráfico da função passa pelos pontos 
e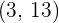 
, sendo a tangente a mesma no ponto de abscissa paralela à bissetriz do primeiro quadrante paralela. Encontre o valor numérico de 
e 
.
Conseguimos equações ao substituir o valor da abscissa em e igualar ao valor da ordenada dos pontos que passam pelo gráfico
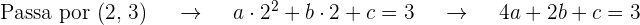
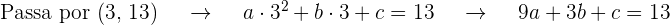
Além do mais a inclinação da tangente é dada
Se a inclinação é no ponto é paralela a bissetriz do quadrante, isso significa que a inclinação é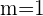 
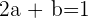
Resolvendo a operação se obtém:
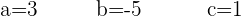
E a equação fica assim
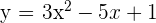
Considerando a função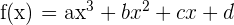 
, determina 
e 
; sabendo-se que a curva passa pelos pontos 
. Além disso as tangentes nos pontos de abscissa e [/latex]-2[/latex] são paralelas ao eixo .
Vamos obter equações ao substituir o valor da abscissa em e igualar ao valor da ordenada dos pontos que passam pelo gráfico
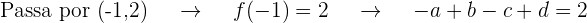
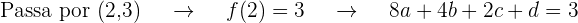
Além do mais, a inclinação da tangente é fornecida como
Se a inclinação no ponto é paralela ao quadrante da bissetriz, isso quer dizer que a inclinação é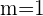
Resolvendo a operação de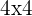 
se obtém:
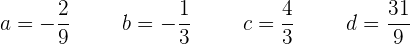
E a equação passa a ficar assim:
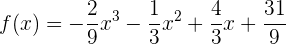
Encontrar o ângulo ou a área
Considerando a função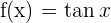 
, encontre o ângulo que forma a reta tangente ao gráfico da função na origem, com o eixo de abscissas.
A reta tangente ao gráfico tem a inclinação de
Na origem essa inclinação é de
Vamos nos lembrar que a inclinação de uma reta é igual a tangente do ângulo que forma com o eixo
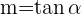
Portanto
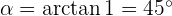
Encontre a área do triângulo determinado pelos eixos de coordenadas e a curva da tangente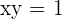 
no ponto .
Se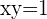 
, então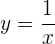 
A inclinação da reta tangente a curva é dada pela derivada
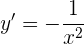
Resolvemos para obter a inclinação em
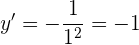
A ordenada do ponto é obtida avaliando na função original
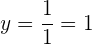
Por fim
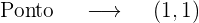
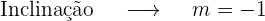
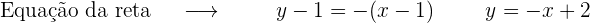
Interseção com o eixo OX
Um vértice é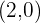 
Interseção com o eixo OY
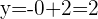
Outro vértice é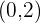 
E a figura fica conforme abaixo
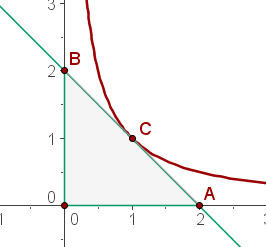
Como se trata de um triângulo retângulo, sua base e sua altura são determinadas pelos catetos, que neste caso ambos medem . A área é de
Gostou desse artigo? Deixe uma nota!
Loading...
