Escreva de todas as formas possíveis a equação da reta que passa pelos pontos  e
e  .
.
Uma reta para nos pontos  e
e  . Portanto, o vetor que une esses dois pontos é:
. Portanto, o vetor que une esses dois pontos é:

Com estes dados já podemos obter as equações da reta (as fórmulas podem ser consultadas em nosso artigo "Resumo de equações da reta").
Equação da reta que passa por 2 pontos:

Equação vetorial:

Equações paramétricas:

Equação da continuidade:

Equação geral:

Equação explícita:

Equação do declive:

De um paralelogramo  conhecemos
conhecemos  . Encontre as coordenadas do vértice D.
. Encontre as coordenadas do vértice D.
Antes de encontrar as coordenadas dos vértices observemos a seguinte figura:

Sabemos que o vetor que vai de  a
a  deve ser igual ao vetor que vai de
deve ser igual ao vetor que vai de  a
a  , ou seja:
, ou seja:

Fazemos os cálculos:

onde  é a coordenada x do ponto
é a coordenada x do ponto  , e
, e  é sua coordenada y. Desse modo, temos:
é sua coordenada y. Desse modo, temos:

Portanto, o ponto  é
é

Classifique o triângulo determinado pelos pontos:  y
y 
Para classificar o triângulo primeiro devemos calcular a distância de cada um de seus lados. Isso fazemos da seguinte maneira:



Note que se cumpre:
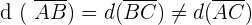
Portanto, o triângulo é isósceles. Além disso, se cumpre

De maneira que o triângulo também é retângulo. Isso pode ser visto na seguinte figura:

Encontre o declive e a ordenada na origem da reta  .
.
Temos a equação  . Isolamos
. Isolamos  da equação:
da equação:

A partir daqui podemos ver que o declive é:
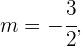
Enquanto que a ordenada da origem é:

Encontre a posição relativa das retas nas seguintes equações:
a. 
b. 
c. 
d. 
Observe que os coeficientes da reta 1 e 2 são proporcionais:

Portanto, a reta 1 e 2 são coincidentes (são a mesma reta).
Da mesma maneira, note que os coeficientes de  e
e  da reta 1 e 3 são proporcionais, no entanto, os termos independentes não são proporcionais:
da reta 1 e 3 são proporcionais, no entanto, os termos independentes não são proporcionais:

Portanto, as retas 1 e 3 são paralelas. Dessa forma, as retas 2 e 3 são paralelas (já que 1 e 2 são iguais).
Por fim, observe que os coeficientes para  e
e  da reta 4 não são proporcionais aos coeficientes de nenhuma outra reta:
da reta 4 não são proporcionais aos coeficientes de nenhuma outra reta:

Portanto, a reta 4 é secante em relação às retas 1, 2 e 3.
Encontre a equação da reta  , que passa
, que passa  , e é paralela à reta
, e é paralela à reta  .
.
Observe a seguinte figura de duas retas paralelas:

Sabemos que duas retas são paralelas se seus declives são o mesmo:

Portanto, a reta  tem a forma (declive):
tem a forma (declive):

Igualando a 0, a reta pode ser escrita como:

Temos um quadrilátero  cujos vértices são
cujos vértices são  e
e 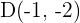 . Comprove que é um paralelogramo e determine o seu centro.
. Comprove que é um paralelogramo e determine o seu centro.
Para que o quadrilátero seja um paralelogramo devemos ter em conta que:  y
y 
Note que:


Portanto, se cumpre  . Por outro lado:
. Por outro lado:

Assim, o quadrilátero é um paralelogramo.
Agora devemos encontrar o ponto médio. Sabemos que as diagonais se cruzam no ponto médio (e este ponto é o centro do paralelogramo), portanto basta encontrar o ponto médio de alguma das diagonais. O ponto médio da diagonal \bar{AC} é

Assim, o centro é o ponto  . Observe a figura do paralelogramo:
. Observe a figura do paralelogramo:

Encontre a equação da reta que passa pelo ponto  e é paralela à reta que une os pontos
e é paralela à reta que une os pontos  e
e  .
.
Se  é a reta que une os pontos então sabemos que a reta
é a reta que une os pontos então sabemos que a reta  que procuramos é paralela a
que procuramos é paralela a  . Portanto, tem o mesmo declive:
. Portanto, tem o mesmo declive:

Se utilizamos a forma declive da reta então a equação da reta  é:
é:
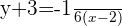
Portanto, a equação de  obteremos igualando a zero:
obteremos igualando a zero:

Os pontos  e
e  , são vértices de um triângulo isósceles
, são vértices de um triângulo isósceles  que tem seu vértice
que tem seu vértice  na reta
na reta  sendo
sendo  e
e  os lados iguais. Calcule as coordenadas do vértice
os lados iguais. Calcule as coordenadas do vértice  .
.
Escrevemos as coordenadas do ponto  como
como  . Como
. Como  , então se cumpre:
, então se cumpre:

Se isolamos  , então
, então

Além disso, os lados  e
e  são iguais, assim se cumpre
são iguais, assim se cumpre  .
.

Se elevamos ao quadrado, temos:

Se substituímos o valor  então temos:
então temos:

Se expandirmos o polinômio e resolvemos a equação "quadrática" (ao final os termos quadráticos se cancelam), então,

Por último, substituindo o valor de  na equação para o de
na equação para o de  temos:
temos:

Portanto, o ponto é  . O gráfico do triângulo é o seguinte:
. O gráfico do triângulo é o seguinte:
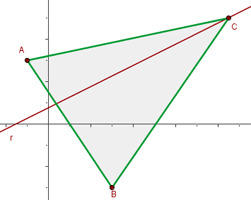
A reta  passa pelo ponto
passa pelo ponto  e é paralela à reta
e é paralela à reta  . Calcule
. Calcule  e
e  .
.
Sabemos que  para em
para em  . Portanto ao substituir as coordenadas do ponto continuamos satisfazendo a igualdade:
. Portanto ao substituir as coordenadas do ponto continuamos satisfazendo a igualdade:

Além disso, sabemos que  , assim sendo, os coeficientes são proporcionais:
, assim sendo, os coeficientes são proporcionais:

Portanto, 
Dado o triângulo  , de coordenadas
, de coordenadas  e
e  ; calcule a equação da mediana que passa pelo vértice
; calcule a equação da mediana que passa pelo vértice  .
.
Temos o seguinte triângulo e desejamos calcular a mediana em um gráfico:

Sabemos que a mediana passará pelo ponto médio do segmento  . Portanto calculamos as coordenadas deste ponto (que indicaremos como
. Portanto calculamos as coordenadas deste ponto (que indicaremos como  ):
):

Agora escrevemos a equação que passa por  e
e  (usamos a fórmula da reta que passa por dois pontos):
(usamos a fórmula da reta que passa por dois pontos):
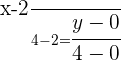
Simplificando um pouco, obtemos a seguinte equação:

De um paralelogramo se conhece um vértice,  , e o ponto de cruzamento das diagonais,
, e o ponto de cruzamento das diagonais,  . Também sabemos que o outro vértice se encontra na origem das coordenadas. Calcule:
. Também sabemos que o outro vértice se encontra na origem das coordenadas. Calcule:
a. Os outros vértices.
b. As equações das diagonais.
c. A longitude das diagonais.
Vamos resolvendo cada um dos enunciados:
a. Os outros vértices:
Sabemos que  é o ponto médio de
é o ponto médio de  , portanto:
, portanto:

Assim continuamos:

Portanto,  . Da mesma maneira,
. Da mesma maneira,  é o ponto médio de
é o ponto médio de  , assim:
, assim:

Assim continuamos:

Desse modo,  . Assim, os quatro vértices são os pontos
. Assim, os quatro vértices são os pontos  e
e  .
.
b. As equações das diagonais.
Neste caso apenas temos que usar a fórmula da reta que passa por dois pontos. Primeiro para a diagonal  :
:

Simplificando um pouco obtemos  . Assim, para a diagonal
. Assim, para a diagonal  temos:
temos:

Que, depois de simplificar, obtemos  .
.
c. A longitude das diagonais.
ara calcular a longitude das diagonais basta calcular a distância entre os vértices apropriados. Para a diagonal  temos:
temos:

Enquanto que para a diagonal  a longitude é:
a longitude é:

O gráfico do paralelogramo é o seguinte:
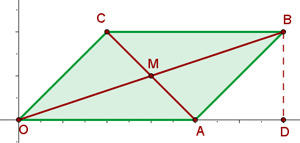
Resumir com IA:


