Temas
- Domínio da função polinomial inteira
- Domínio da função racional
- Domínio de uma função radical com índice ímpar
- Domínio de uma função radical com índice par
- Domínio de uma função logarítmica
- Domínio de uma função exponencial
- Domínio de uma função seno
- Domínio de uma função cosseno
- Domínio de uma função tangente
- Domínio de uma função cotangente
- Domínio de uma função secante
- Domínio de uma função cossecante
- Domínio de operações com funções
O domínio de uma função está formado por todos os elementos que têm imagem.
Isto é, são os valores de  que podemos substituir na regra de correspondência de uma função para obter o valor correspondente de
que podemos substituir na regra de correspondência de uma função para obter o valor correspondente de  .
.
Matematicamente, podemos expressar:
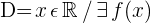
que significa que o domínio de uma função são aqueles valores de  que pertencem aos números reais para os quais existe um valor associado da função
que pertencem aos números reais para os quais existe um valor associado da função  .
.
O subconjunto dos números reais do qual se define a função chama-se domínio ou campo de existência da função.
É indicado por D.
A variável x pertencente ao domínio função recebe o nome de variável independente.
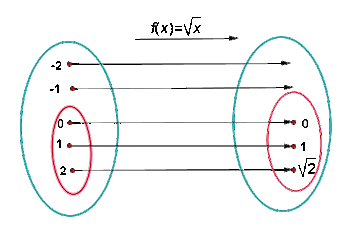
Conjunto inicial - Conjunto final
Domínio - Conjunto imagem ou campo

Domínio da função polinomial inteira
O domínio de uma função polinomial é  , porque qualquer número real tem imagem.
, porque qualquer número real tem imagem.
Também são funções polinomiais inteiras as que têm um número (uma constante) no denominador:
Exemplo de domínios das funções polinomiais
1 

2 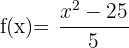

Observe que ao substituir qualquer valor de  nas funções, sempre obteremos um valor correspondente para
nas funções, sempre obteremos um valor correspondente para  .
.
Domínio da função racional
O domínio é  menos os valores que anulam o denominador (não pode existir uma fração cujo denominador seja zero).
menos os valores que anulam o denominador (não pode existir uma fração cujo denominador seja zero).
Exemplo de exercício de domínio da função racional
1 Qual é o domínio da função 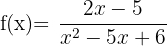 ?
?
Igualamos o denominador a  e resolvemos a equação
e resolvemos a equação

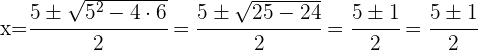


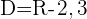
Domínio de uma função radical com índice ímpar
O domínio é o domínio da função radicando.
1 

2 
Domínio de uma função radical com índice par
O domínio está formado por todos os valores do radicando que fazem com que este seja maior ou igual a zero.
1 


2 
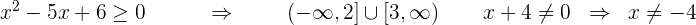

3 Qual é o domínio da função ?
?
Neste caso, o denominador deve ser maior que zero e, além disso, devemos procurar os valores de  para que a raiz exista, assim:
para que a raiz exista, assim:




4 Determine o domínio da função  .
.
O radicando tem que ser maior que zero e o denominador diferente de zero



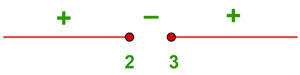
5 Obtenha o domínio da função  .
.
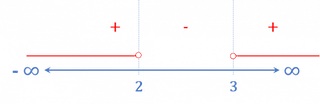
Como o radicando deve ser maior ou igual que zero, utilizamos a desigualdade:

Fazemos a inequação de segundo grau


As raízes da equação de segundo grau associada à desigualdade são:  e
e 
Assim, os intervalos em que a desigualdade é cumprida são:
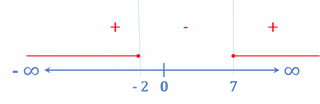
O domínio formam os valores menores que -2 e maiores que 7, incluindo-os.

6 Obtenha o domínio da função 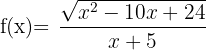 .
.
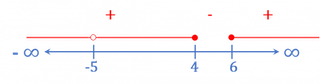
Neste caso duas condições devem ser cumpridas, uma para o quociente e outra para a raiz, dessa forma o numerador tem que ser maior ou igual a zero e o denominador diferente de zero. Assim:



Domínio de uma função logarítmica
O domínio está formado por todos os valores que fazem com que a função que aparece dentro do logaritmo seja maior que zero.

Deve cumprir:

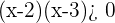

Domínio de uma função exponencial
Exemplos de domínio de funções exponenciais
1 

2 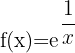
O domínio é igual a  menos os valores que anulam o denominador do expoente
menos os valores que anulam o denominador do expoente

3 
O domínio coincide com o campo de existência real da raiz

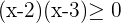



Domínio de uma função seno
O domínio de uma função seno é 
Domínio de uma função cosseno
O domínio de uma função cosseno é 
Domínio de uma função tangente
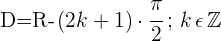
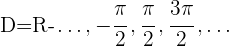
Domínio de uma função cotangente
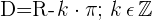
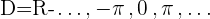
Domínio de uma função secante
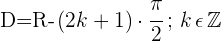
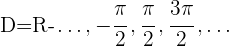
Domínio de uma função cossecante
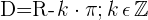
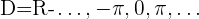
Domínio de operações com funções

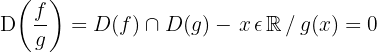

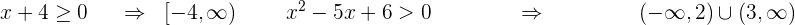

Resumir com IA:













