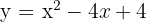Temas
Antes de começar com os exercícios é importante lembrar o básico.

O que é uma função quadrática?
Uma função quadrática é uma função polinomial de segundo grau e sua regra correspondência é 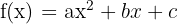 , onde
, onde  são constantes reais e
são constantes reais e 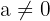
O gráfico de uma função quadrática é uma cônica (círculo, elipse, parábola ou hipérbole),
mas nesta seção vamos resolver apenas funções quadráticas de parábolas.
O gráfico de  (a função quadrática mais simples), permite observar algumas características das parábolas. Entre outras coisas,
(a função quadrática mais simples), permite observar algumas características das parábolas. Entre outras coisas,  e
e 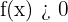 para qualquer outro valor real de
para qualquer outro valor real de  . Portanto, a função tem um mínimo no ponto
. Portanto, a função tem um mínimo no ponto  , que se chama vértice da parábola.
, que se chama vértice da parábola.
Se  a parábola se encontra na parte inferior (abre para cima)
a parábola se encontra na parte inferior (abre para cima)
Se  , a parábola se encontra na parte superior (abre para baixo)
, a parábola se encontra na parte superior (abre para baixo)
Como resolver e representar uma função quadrática?
Existem dois métodos para resolver e representar uma função quadrática. A seguinte detalharemos os passos de cada um:
Fórmula do vértice
1Encontre os valores de  .
.
2Encontre o valor  do vértice com a fórmula do vértice.
do vértice com a fórmula do vértice.
3Encontre o valor de  substituindo o valor de
substituindo o valor de 
4Escreva as coordenadas  .
.
Resolver o quadrado
1Escreva a equação.
2Divida pelo valor do termo  .
.
3Passe a constante da equação para a direita.
4Complete o quadrado ao lado esquerdo da equação.
5Fatorize o lado esquerdo da equação.
6Encontre e escreva as coordenadas  .
.
Propostas de exercícios
Resolva e represente as seguintes funções quadráticas

1) Vértice
Aplicamos a fórmula do vértice
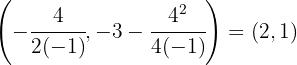
Assim, o vértice é 
2) Ponto de interseção com o eixo 
Igualamos a função a zero e calculamos suas soluções
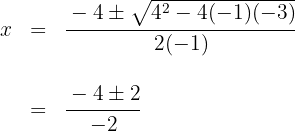
Obtemos as soluções 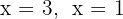
Assim, as interseções com o eixo  são
são  e
e 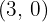
3) Ponto de interseção com o eixo 
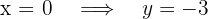
Assim, a interseção com o eixo  é
é 
4) Com os dados anteriores, a representação gráfica é:
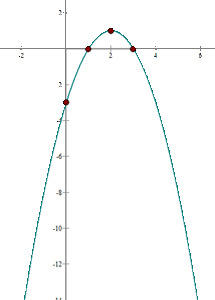
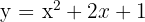
1) Vértice
Aplicamos a fórmula do vértice

Assim, o vértice é 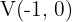
2) Ponto de interseção com o eixo 
Igualamos a função a zero e calculamos suas soluções
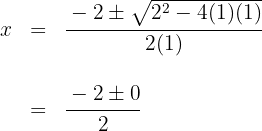
Obtemos a solução 
Assim, a interseção com o eixo  é
é 
3) Ponto de interseção com o eixo 

Assim, a interseção com o eixo  é
é 
4) Com os dados anteriores, a representação gráfica é:
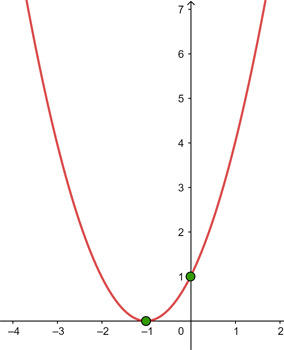

1) Vértice
Aplicamos a fórmula do vértice
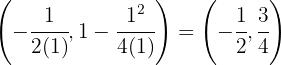
Assim, o vértice é 
2) Ponto de interseção com o eixo 
Igualamos a função a zero e calculamos suas soluções
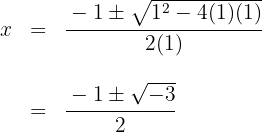
Como o discriminante é negativo,  , não há interseção com o eixo
, não há interseção com o eixo  é
é 
3) Ponto de interseção com o eixo 

Assim, a interseção com o eixo  é
é 
4) Com os dados anteriores, a representação gráfica é:
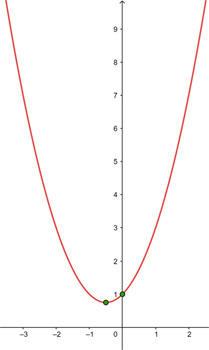
Encontre o vértice e a equação do eixo de simetria das seguintes parábolas:
O vértice da parábola  é dado por
é dado por 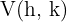 e o eixo de simetria por
e o eixo de simetria por  .
.
a) Para a parábola 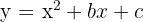 , o vértice é dado por
, o vértice é dado por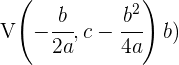 2
2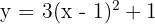
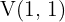

c) 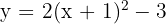


d) 


e) 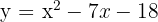
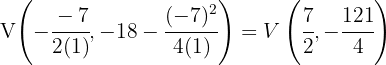
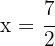
f) 
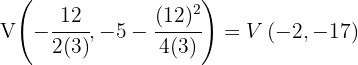

Indique, sem desenhar, em quantas interseções são cortadas o eixo de abscissas pelas seguintes parábolas:
Aplicamos o determinante  e a partir de seu sinal concluímos se as parábolas cortam vezes vez ou nenhuma vez o eixo das abscissas.
e a partir de seu sinal concluímos se as parábolas cortam vezes vez ou nenhuma vez o eixo das abscissas.
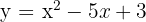 Calculamos o determinante de:
Calculamos o determinante de:  Como o determinante é positivo, temos dois pontos de interseção.
Como o determinante é positivo, temos dois pontos de interseção.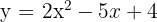 Calculamos o determinante:
Calculamos o determinante: 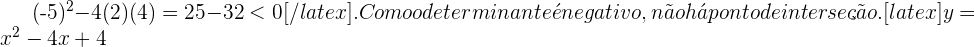 . Calculamos o determinante de
. Calculamos o determinante de 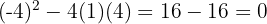 . Como o determinante é zero, há um ponto de interseção.
. Como o determinante é zero, há um ponto de interseção. . Calculamos o determinante
. Calculamos o determinante 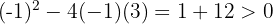 . Como o determinante é positivo, há dois pontos de interseção.
. Como o determinante é positivo, há dois pontos de interseção.
Para a equação \( y = x^2 - 4x + 4 \), calculamos o determinante de \( (-4)^2 - 4(1)(4) = 16 - 16 = 0 \). Como o determinante é zero, há um ponto de interseção.
Para a equação \( y = -x^2 - x + 3 \), calculamos o determinante \( (-1)^2 - 4(-1)(3) = 1 + 12 > 0 \). Como o determinante é positivo, há dois pontos de interseção.
Uma função quadrática tem uma expressão na fórmula  e passa pelo ponto
e passa pelo ponto  . Calcule o valor de
. Calcule o valor de  .
.
Substituímos o ponto na função 2Resolvemos
2Resolvemos 
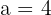
Sabe-se que a função quadrática da fórmula  passa pelos pontos
passa pelos pontos  e
e  . Calcule
. Calcule 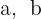 e
e  .
.
- Substituímos o valor de cada ponto em


- Obtemos o seguinte sistema de equações

- Resolvendo o sistema de equações obtemos

Uma parábola tem seu vértice no ponto 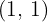 e passa pelo ponto
e passa pelo ponto  . Encontre sua equação.
. Encontre sua equação.
1A equação é expressa pela fórmula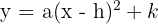 2Substituímos os valores do vértice
2Substituímos os valores do vértice
3Substituímos os valores do ponto  por onde passa e isolamos
por onde passa e isolamos 
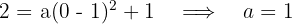
4Substituímos o valor de  e resolvemos
e resolvemos
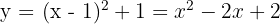
Partindo do gráfico da função  , represente:
, represente:
Usaremos o gráfico 
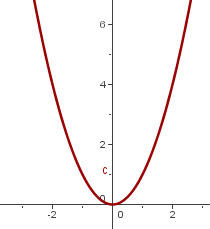
a) 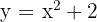 Passamos o gráfico de
Passamos o gráfico de  de maneira que o vértice se encontre em
de maneira que o vértice se encontre em  :
:
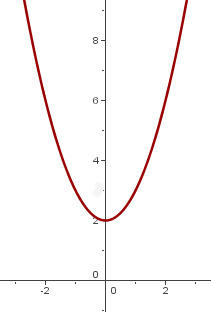
b) 
Passamos o gráfico de  de maneira que o vértice se encontre em
de maneira que o vértice se encontre em 
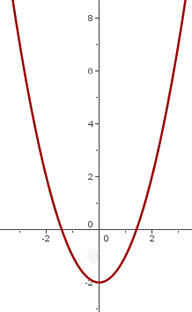
c) 
Passamos o gráfico de  de maneira que o vértice se encontre em
de maneira que o vértice se encontre em 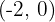
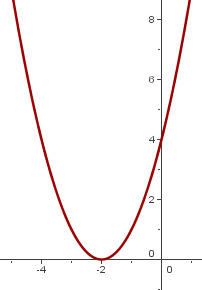
d) 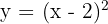
Passamos o gráfico de  de maneira que o vértice se encontre em
de maneira que o vértice se encontre em 
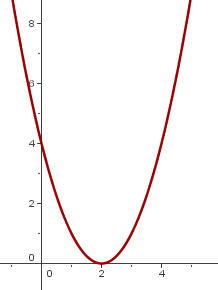
e) 
Passamos o gráfico de  de maneira que o vértice se encontre em
de maneira que o vértice se encontre em 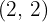
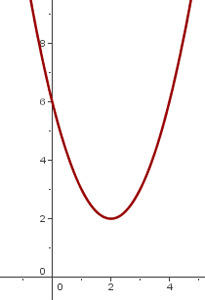
f) 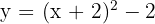
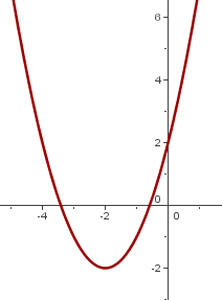
Passamos o gráfico de  de maneira que o vértice se encontre em
de maneira que o vértice se encontre em 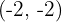
Resumir com IA: