Temas
- Tabela da distribuição normal
- Variável aleatória em distribuição normal
- Distribuição normal, média e desvio padrão
- Distribuição normal aplicada à temperatura ambiental
- Distribuição normal aplicada ao peso dos alunos
- Distribuição normal para aplicar provas
- Distribuição normal para classificar grupos
- Cálculo de coeficiente intelectual através de distribuição normal
- Uso da distribuição normal para calcular probabilidade
- Probabilidade de um evento com variável aleatória
- Distribuição normal para probabilidade

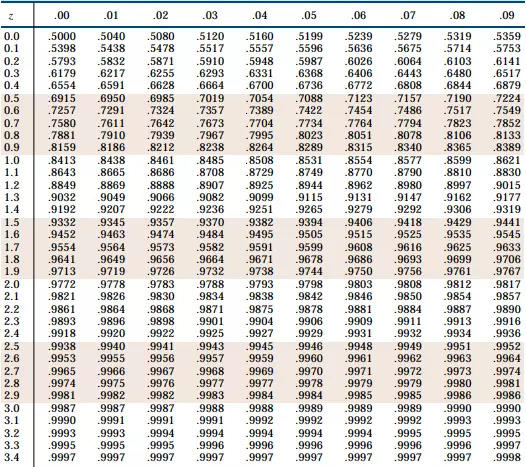
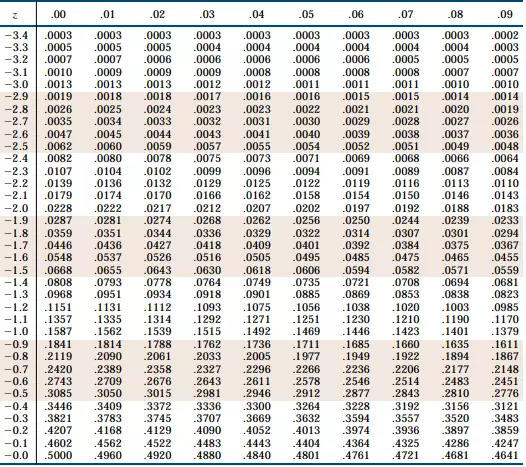
Tabela da distribuição normal
A tabela de distribuição normal é utilizada para localizar valores definidos para a variável z.
Variável aleatória em distribuição normal
Se  é uma variável aleatória de uma distribuição
é uma variável aleatória de uma distribuição 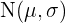 , encontre:
, encontre:  .
.
Se  é uma variável aleatória de uma distribuição
é uma variável aleatória de uma distribuição 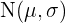 , encontre:
, encontre:  .
.
Neste caso, estamos utilizando uma distribuição normal estândar. Para resolver o problema usaremos a seguinte fórmula:
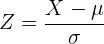
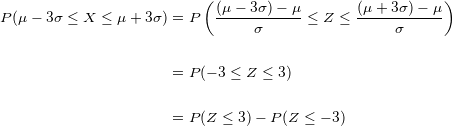
Agora temos que localizá-lo em nossa tabela de distribuição normal. Localizamos o valor quando 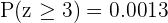 , mas precisamos do valor quando
, mas precisamos do valor quando 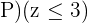 , então utilizamos
, então utilizamos 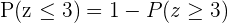 obtemos
obtemos  . Além disso, como a distribuição normal é simétrica, então
. Além disso, como a distribuição normal é simétrica, então  .
.
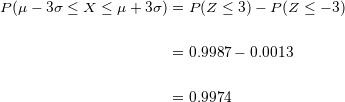
Quer dizer que, aproximadamente 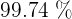 dos valores de
dos valores de  estão a menos de três desvios padrão da média.
estão a menos de três desvios padrão da média.
Distribuição normal, média e desvio padrão
Em uma distribuição normal de média  e desvio normal
e desvio normal  , calcule o valor de a para que:
, calcule o valor de a para que: 
Em uma distribuição normal de média  e desvio normal
e desvio normal  , calcule o valor de a para que:
, calcule o valor de a para que: 
Utilizando a fórmula 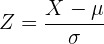 , vamos substituir o valor da média (
, vamos substituir o valor da média ( 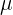 ), e o desvio padrão (
), e o desvio padrão ( 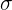 ).
).
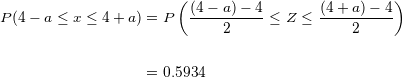
Ao simplificarmos, obtemos:
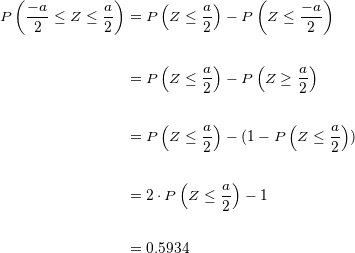
Onde continuamos

Agora devemos localizar na tabela de distribuição normal o valor 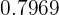 e observamos que corresponde a
e observamos que corresponde a  , então:
, então:

Distribuição normal aplicada à temperatura ambiental
Em uma cidade se estima que a temperatura máxima no mês de junho se mantém em uma distribuição normal com média de 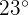 e desvio padrão de
e desvio padrão de 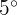 .
.
Calcule o número de dias do mês dos quais se esperam atingir máximas entre 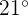 e
e 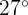 .
.
Em uma cidade se estima que a temperatura máxima no mês de junho se mantém em uma distribuição normal com média de 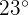 e desvio padrão de
e desvio padrão de 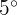 .
.
Calcule o número de dias do mês dos quais se esperam atingir máximas entre 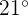 e
e 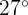 .
.
Utilizando a fórmula 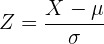 , vamos substituir o valor da média (
, vamos substituir o valor da média ( ), e o desvio padrão (
), e o desvio padrão (  ).
).
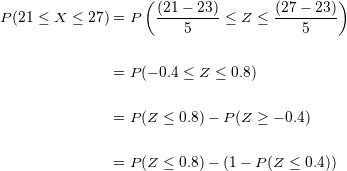
Procuramos os valores correspondentes na tabela de distribuição normal:

Portanto
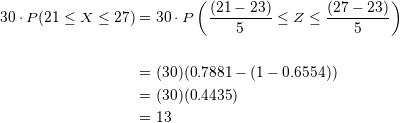
Isso quer dizer que durante todo o mês apenas  dias alcançarão temperaturas entre
dias alcançarão temperaturas entre  e
e  graus.
graus.
Distribuição normal aplicada ao peso dos alunos
A média do peso de  alunos de um colégio é
alunos de um colégio é 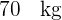 e o desvio padrão de
e o desvio padrão de 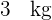 .
.
Supondo que os pesos são distribuídos normalmente, encontre quantos alunos pesam:
1. Entre 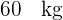 e
e  .
.
2. Mais de  .
.
3. Menos de  .
.
4.  .
.
5.  ou menos.
ou menos.
A média do peso de  alunos de um colégio é
alunos de um colégio é 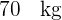 e o desvio padrão de
e o desvio padrão de 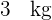 .
.
Supondo que os pesos são distribuídos normalmente, encontre quantos alunos pesam:
1 Entre 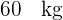 e
e  .
.
Substituindo:
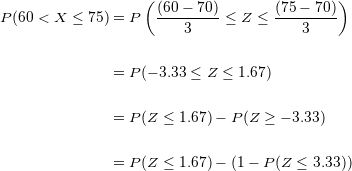
Localizando os valores na tabela de distribuição normal e operando:

Portanto, se multiplicarmos a probabilidade 
Dos  alunos
alunos  estão entre
estão entre  e
e  quilos.
quilos.
2 Mais de  .
.
Substituindo e simplificando temos:
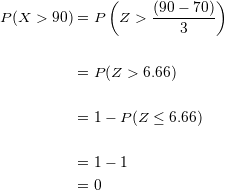
Multiplicando a probabilidade por  obtemos
obtemos
 .
.
É impossível encontrar algum aluno acima dos  quilos.
quilos.
3 Menos de  .
.
Substituindo e simplificando temos:
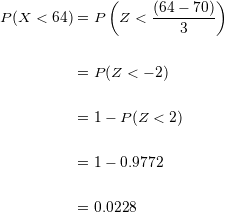
Multiplicando a probabilidade por  obtemos
obtemos
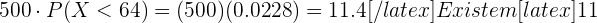 alunos que pesam menos de
alunos que pesam menos de  quilos
quilos
4  .
.
Quando a distribuição é contínua a probabilidade de que a variável tenha um valor exato é sempre nula ( ). Portanto
). Portanto
 .
.
5  ou menos.
ou menos.
Dados os resultados anteriores:
Existem zero alunos que pesam  quilos exatos e há
quilos exatos e há  alunos que pesam menos de
alunos que pesam menos de  quilos, portanto, existem
quilos, portanto, existem  alunos que pesam
alunos que pesam  quilos ou menos.
quilos ou menos.
 \displaystyle 500 \cdot P(X < 64) = 500 \cdot P(X \leq 64) = 11[/latex].
\displaystyle 500 \cdot P(X < 64) = 500 \cdot P(X \leq 64) = 11[/latex].
Distribuição normal para aplicar provas
Supõe-se que os resultados de uma prova mantém uma distribuição normal com média de 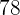 e desvio padrão de
e desvio padrão de  .
.
Se pede:
1. Qual é a probabilidade de que uma pessoa que faça a prova obtenha uma qualificação superior a  ?
?
2. Calcule a proporção de alunos que têm uma pontuação que exceda em, pelo menos, cinco pontos a marca entre apto e não-apto (são declarados não-aptos 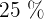 dos alunos que tiveram os pontos mais baixos)
dos alunos que tiveram os pontos mais baixos)
3. Sabendo que a qualificação de um aluno é maior do que  , qual é a probabilidade de que sua qualificação seja de fato superior a
, qual é a probabilidade de que sua qualificação seja de fato superior a  ?
?
Supõe-se que os resultados de uma prova mantém uma distribuição normal com média de 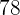 e desvio padrão de
e desvio padrão de  .
.
Se pede:
1. Qual é a probabilidade de que uma pessoa que faça a prova obtenha uma qualificação superior a  ?
?
Substituímos os valores na fórmula:
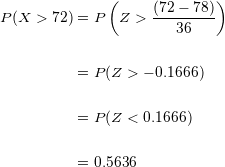
A probabilidade de que uma pessoa obtenha uma pontuação maior do que  ao fazer a prova é de
ao fazer a prova é de 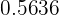 .
.
2 Calcule a proporção de alunos que têm uma pontuação que exceda em pelo menos cinco pontos a marca entre apto e não-apto (são declarados não-aptos 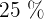 dos alunos que tiveram os pontos mais baixos).
dos alunos que tiveram os pontos mais baixos).
Substituímos os valores na fórmula:
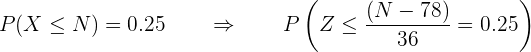
Localizamos a probabilidade  na tabela de distribuição normal, que é
na tabela de distribuição normal, que é 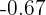 . Isto significa que
. Isto significa que
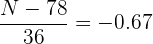
Isolamos  :
:
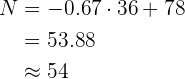
Calculamos 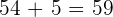 :
:
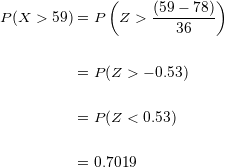
A porcentagem de alunos que são aptos e que excedem em  pontos a marca de não-aptos é de
pontos a marca de não-aptos é de  .
.
3 Sabendo que a qualificação de um aluno é maior do que  , qual é a probabilidade de que sua qualificação seja de fato superior a
, qual é a probabilidade de que sua qualificação seja de fato superior a  ?
?
Substituímos:
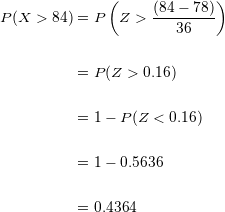
Com o primeiro cálculo deste exercício sabemos que a probabilidade de que um aluno obtenha uma pontuação maior do que  pontos ao fazer a prova é de
pontos ao fazer a prova é de 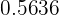 .
.
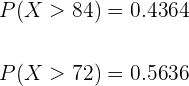
Agora utilizaremos a fórmula de probabilidade condicional:
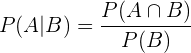
Substituímos:
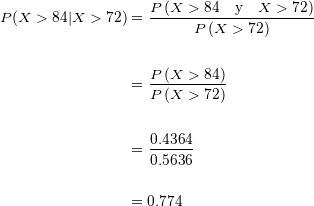
A probabilidade de que um aluno que obteve uma pontuação maior do que  tenha conseguido de fato uma pontuação acima de
tenha conseguido de fato uma pontuação acima de  é de
é de  .
.
Distribuição normal para classificar grupos
Após um teste de cultura geral podemos observar que os pontos obtidos mantém uma distribuição 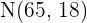 .
.
Desejamos classificar os examinados em três grupos (de baixa cultural geral, de cultura geral aceitável e de excelente cultura geral) de modo que no primeiro grupo estejam 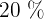 dos examinados,
dos examinados,  no segundo grupo e
no segundo grupo e  no terceiro grupo.
no terceiro grupo.
Quais são as pontuações que marcam a transição de um grupo ao outro?
Após um teste de cultura geral podemos observar que os pontos obtidos mantém uma distribuição 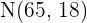 .
.
Desejamos classificar os examinados em três grupos (de baixa cultural geral de cultura geral aceitável e de excelente cultura geral) de modo que no primeiro grupo estejam 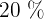 dos examinados,
dos examinados,  no segundo grupo e
no segundo grupo e  no terceiro grupo.
no terceiro grupo.
Quais são as pontuações que marcam a transição de um grupo ao outro?

Localizamos na nossa tabela o parâmetro correspondente à probabilidade  , que é
, que é  :
:

Desse modo, se  . Então
. Então
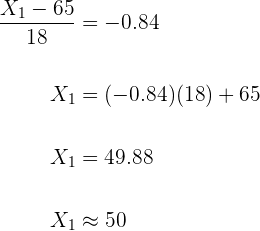
Agora localizamos na tabela o parâmetro para a probabilidade de  , que é
, que é 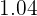 . O que significa que
. O que significa que

Desse modo, se 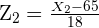 . Então
. Então
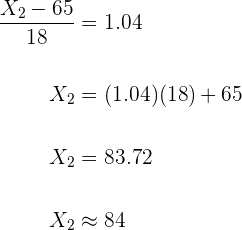
De baixa cultura até  pontos.
pontos.
De cultural aceitável entre  e
e  .
.
De excelente cultura a partir de  pontos.
pontos.
Cálculo de coeficiente intelectual através de distribuição normal
Vários testes de inteligência deram uma pontuação que mantém uma lei normal com média de  e desvio padrão de
e desvio padrão de  .
.
1 Determine a porcentagem de examinados que obteriam um coeficiente entre  e
e  .
.
2 Qual o intervalo centrado em  que contém
que contém 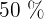 dos examinados?
dos examinados?
3 Em uma população de 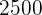 indivíduos, se espera que quantos obtenham um coeficiente superior a
indivíduos, se espera que quantos obtenham um coeficiente superior a  ?
?
Vários testes de inteligência deram uma pontuação que mantém uma lei normal com média de  e desvio padrão de
e desvio padrão de  .
.
1 Determine a porcentagem de examinados que obteriam um coeficiente entre  e
e  .
.
Substituímos os valores na fórmula:
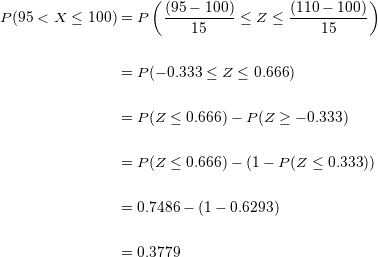
A porcentagem de examinados que obteriam uma pontuação entre  e
e  é de
é de  .
.
2 Qual o intervalo centrado em  que contém
que contém 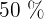 dos examinados?
dos examinados?

Como queremos pegar 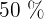 do centro de examinados, então devemos pegar o intervalo que está entre
do centro de examinados, então devemos pegar o intervalo que está entre 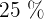 e
e 
Localizamos na tabela o parâmetro para a probabilidade de  e de
e de 
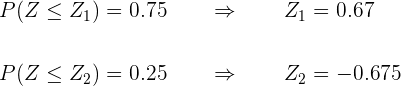
Substituímos e isolamos
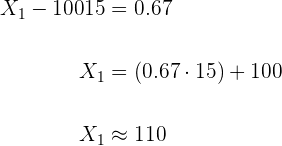
e
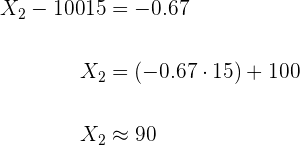
Então o intervalo é: 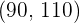 .
.
O intervalo centrado que contém 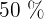 dos examinados obterá uma pontuação entre
dos examinados obterá uma pontuação entre  e
e  .
.
3 Em uma população de 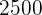 indivíduos, se espera que quantos obtenham um coeficiente superior a
indivíduos, se espera que quantos obtenham um coeficiente superior a  ?
?
Substituímos os valores na fórmula, calculamos o parâmetro e localizamos a probabilidade na tabela

Multiplicando esta probabilidade pelos 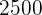 indivíduos, obtemos
indivíduos, obtemos
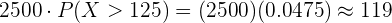
Em uma população de 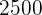 indivíduos, se espera que
indivíduos, se espera que 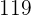 deles tenham um coeficiente superior a
deles tenham um coeficiente superior a  .
.
Uso da distribuição normal para calcular probabilidade
Em uma cidade, uma em cada três famílias possuem telefone.
Se escolhemos  famílias ao acaso, calcule a probabilidade de que entre elas existam pelo menos
famílias ao acaso, calcule a probabilidade de que entre elas existam pelo menos  com telefone.
com telefone.
Em uma cidade, uma em cada três famílias possuem telefone.
Se escolhemos  famílias ao acaso, calcule a probabilidade de que entre elas existam pelo menos
famílias ao acaso, calcule a probabilidade de que entre elas existam pelo menos  com telefone
com telefone
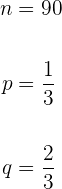
n: Quantidade de famílias para escolher.
p: Probabilidade de escolher uma família que tenha telefone.
q: Complemento da probabilidade.
Para resolver este tipo de exercício usaremos o Teorema de Moivre-Laplace para Probabilidade:.
Se  é uma variável aleatória binomial de parâmetros
é uma variável aleatória binomial de parâmetros  y
y ,
, 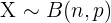 , então
, então  pode ser aproximado de uma distribuição normal de média
pode ser aproximado de uma distribuição normal de média  e desvio padrão
e desvio padrão 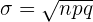 (onde
(onde 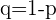 ) se se cumpre as duas condições seguintes:
) se se cumpre as duas condições seguintes:
Condição 1.  .
.
Condição 2. 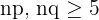 .
.
Então, a variável binomial 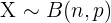 ficaria aproximada pela variável normal
ficaria aproximada pela variável normal  .
.
Como  , é cumprida a condição 1.
, é cumprida a condição 1.
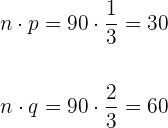
Então, é cumprida a condição 2.
Então utilizamos a fórmula  .
.
Substituímos os dados:

Agora utilizamos a fórmula de distribuição normal
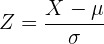
Substituímos, operamos e localizamos o valor da probabilidade na nossa tabela de distribuição normal:
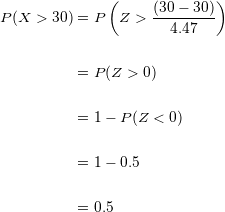
Ao escolher  famílias ao acaso, existe uma probabilidade de
famílias ao acaso, existe uma probabilidade de  de que pelo menos
de que pelo menos  famílias possuam um telefone.
famílias possuam um telefone.
Probabilidade de um evento com variável aleatória
Em uma prova há  perguntas de múltipla escolha. Cada pergunta tem uma resposta correta e uma incorreta.
perguntas de múltipla escolha. Cada pergunta tem uma resposta correta e uma incorreta.
Estará aprovado quem responde mais de  respostas corretas.
respostas corretas.
Supondo que as perguntas sejam respondidas ao acaso, calcule a probabilidade de aprovação na prova.
Em uma prova há  perguntas de múltipla escolha. Cada pergunta tem uma resposta correta e uma incorreta.
perguntas de múltipla escolha. Cada pergunta tem uma resposta correta e uma incorreta.
Estará aprovado quem responde mais de  respostas corretas.
respostas corretas.
Supondo que as perguntas sejam respondidas ao acaso, calcule a probabilidade de aprovação na prova
Utilizamos o Teorema de Moivre-Laplace para Probabilidade:
Comprovamos as  condições:
condições:
Primeira condição:
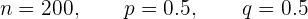
Segunda condição: 
Como ambas condições se cumprem, usaremos a fórmula
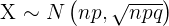 .
.
Substituímos:
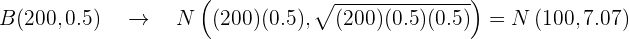
Agora utilizaremos 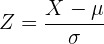
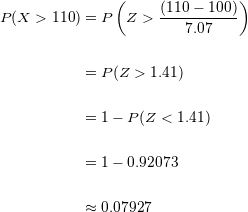
Ao responder ao acaso em uma prova de múltipla escolha existe a probabilidade de 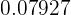 de aprovação.
de aprovação.
Distribuição normal para probabilidade
Um estudo mostrou que em um bairro,  dos lares têm pelo menos duas televisões. Escolhemos ao acaso uma amostra de
dos lares têm pelo menos duas televisões. Escolhemos ao acaso uma amostra de  lares em tal bairro.
lares em tal bairro.
Se pede:
1 Qual é a probabilidade de que pelo menos  dos lares citados tenham ao menos duas televisões?
dos lares citados tenham ao menos duas televisões?
2 Qual é a probabilidade de que entre  e
e  de lares tenham ao menos duas televisões?
de lares tenham ao menos duas televisões?
Um estudo mostrou que em um bairro,  têm pelo menos duas televisões. Escolhemos ao acaso uma amostra de
têm pelo menos duas televisões. Escolhemos ao acaso uma amostra de  lares em tal bairro.
lares em tal bairro.
Se pide:
1 Qual é a probabilidade de que pelo menos  dos lares citados tenham ao menos duas televisões?
dos lares citados tenham ao menos duas televisões?
Utilizamos o Teorema de Moivre-Laplace para Probabilidade. Comprovamos se se cumprem as  condições:
condições:
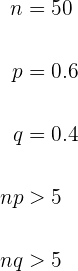
Como ambas condições são cumpridas, usaremos a fórmula  .
.
Substituímos:
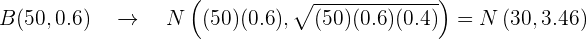
Agora utilizaremos 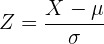 .
.
Substituímos:
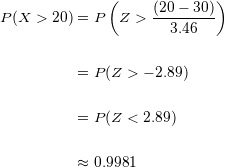
2 Qual é a probabilidade de que entre  e
e  dos lares tenham ao menos duas televisões?
dos lares tenham ao menos duas televisões?
Utilizando a fórmula 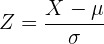 , vamos substituir o valor da média
, vamos substituir o valor da média  e o desvio padrão
e o desvio padrão 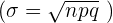
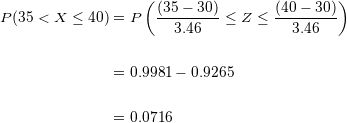
A probabilidade de que entre  e
e  lares tenham ao menos
lares tenham ao menos  televisões é de
televisões é de  .
.
Resumir com IA:












