Temas
- Quantos comitês de alunos podem ser formados?
- Combinações com as cores do arco-íris
- Calcule o número de cumprimentos em uma reunião
- Combinações com quatro garrafas
- Combinações possíveis na loteria nacional
- Quantidade de triângulos em um pentágono
- Combinações com condições
- Combinações com moedas
- Equações com combinações

Quantos comitês de alunos podem ser formados?
Em uma turma de  alunos querem escolher um comitê formado por três alunos.
alunos querem escolher um comitê formado por três alunos.
Quantos comitês diferentes podem ser formados?
Em uma turma de  alunos querem escolher um comitê formado por três alunos.
alunos querem escolher um comitê formado por três alunos.
Quantos comitês diferentes podem ser formados?
Primeiro, devemos ter em conta que:
Não entram todos os elementos. Isso porque vamos pegar apenas  alunos entre os
alunos entre os  .
.
Não importa a ordem. Isso porque dá no mesmo escolher João, Maria e Cíntia ou escolher Cíntia, João e Maria. Apenas importa quem conforma o comitê e não a ordem como sejam escolhidos.
Não repetem-se os elementos. Isso porque obviamente não podemos escolher mais de uma vez uma pessoa. Uma vez que alguém é escolhido, ele ou ela já não pertencem ao grupo de alunos restantes.
Dito isso, fica claro que estamos frente a um problema do qual podemos resolver com combinações da seguinte maneira
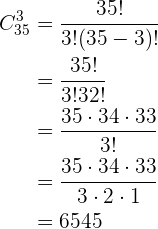
Combinações com as cores do arco-íris
Dadas as cores do arco-íris, quantos grupos de três cores podemos formar com elas?
Dadas as cores do arco-íris, quantos grupos de três cores podemos formar com elas?
Para resolver este problema primeiro devemos notar o seguinte:
Não entram todos os elementos. Isso porque vamos usar apenas  das
das  cores do arco-íris.
cores do arco-íris.
Não importa a ordem. Isso porque apenas as cores que escolhemos é importante e não a ordem em que escolhemos elas.
Não repetem-se os elementos. Está claro que não podemos escolher mais de uma vez uma cor. Ao ser escolhida essa cor, já não é mais considerada para a próxima seleção. Poderíamos dizer que ela já está fora do conjunto.
Dito isso, fica claro que este problema pode ser resolvido utilizando a fórmula de combinações:
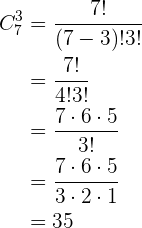
Calcule o número de cumprimentos em uma reunião
Em uma reunião de  pessoas trocam-se cumprimentos entre todos.
pessoas trocam-se cumprimentos entre todos.
Quantos cumprimentos foram trocados?
Em uma reunião de  pessoas trocam-se cumprimentos entre todos.
pessoas trocam-se cumprimentos entre todos.
Quantos cumprimentos foram trocados?
Devemos notar o seguinte:
Não entram todos os elementos. Isso porque um cumprimento pode ser analisado como um grupo de duas pessoas (já que apenas pode ser feito entre duas pessoas).
Não importa a ordem. Isso porque dá no mesmo que João tenha cumprimentado Maria ou que Maria tenha cumprimentado João.
Não repetem-se os elementos. Devemos ter em conta que a premissa de que os elementos se repetem seria como pensar que uma pessoa pode cumprimentar a si mesma, o que não teria sentido.
Dito isso, fica claro que este problema pode ser resolvido utilizando a fórmula de combinações:
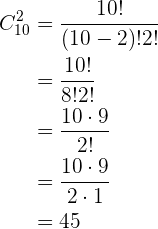
Combinações com quatro garrafas
Em uma barraca vendem-se cinco sabores diferentes de suco. Deseja-se comprar  , sem se importar que sejam escolhidos vários do mesmo sabor.
, sem se importar que sejam escolhidos vários do mesmo sabor.
De quantas formas podemos escolher os sabores de suco?
Em uma barraca vendem-se cinco sabores diferentes de suco. Deseja-se comprar  , sem se importar que sejam escolhidos vários do mesmo sabor.
, sem se importar que sejam escolhidos vários do mesmo sabor.
De quantas formas podemos escolher os sabores de suco?
Primeiro devemos notar os seguintes dados:
Não entram todos os elementos. Isso porque existem cinco sabores, mas queremos apenas  .
.
Não importa a ordem. Da igual se escolhemos duas bebidas sabor cola e dois sucos sabor maçã,
ou dois sucos sabor maçã e depois duas bebidas sabor cola.
Sim repetem-se os elementos. Isso porque podemos escolher quatro sabores diferentes ou quatro iguais, etc.
Dito isso, fica claro que usaremos combinações com repetição, assim, aplicando a fórmula, temos o seguinte resultado/p>
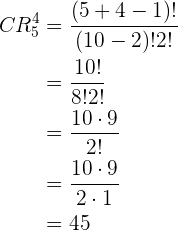
Combinações possíveis na loteria nacional
Quantas apostas de seis números em um jogo de Loteria com 49 números devem ser feitas para garantir o acerto dos seis números premiados entre os  ?
?
Quantas apostas de seis números em um jogo de Loteria com 49 números devem ser feitas para garantir o acerto dos seis números premiados entre os  ?
?
Devemos notar o seguinte:
Não entram todos os elementos. Isso porque vamos escolher apenas  entre
entre  elementos.
elementos.
Não importa a ordem. Neste caso, importa apenas os elementos que escolhemos, mas não sua ordem.
Não repetem-se os elementos. Isso porque não podemos escolher várias vezes o mesmo elemento.
Dito isso, fica claro que este problema pode ser resolvido utilizando a fórmula de combinações:
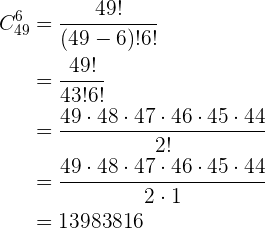
Quantidade de triângulos em um pentágono
Quantas diagonais têm um pentágono e quantos triângulos podem ser formados com seus vértices?
Quantas diagonais têm um pentágono e quantos triângulos podem ser formados com seus vértices?
Primeiro, precisamos determinar as retas que podem ser traçadas entre 2 vértices. Devemos notar que temos 5 vértices e que cada reta pode ser determinada como o par de vértices que a define, portanto, teríamos combinações.
Não entram todos os elementos. Isso porque uma reta é definida apenas por  dos
dos  vértices.
vértices.
Não importa a ordem. Uma reta é definida porque une dois vértices, mas não há nenhuma direção. Dessa forma, não importa qual vértice consideremos primeiro.
Não repetem-se os elementos. Isso porque considerar a repetição de elementos seria considerar retas que vão de um ponto a si mesmo, e isso não teria sentido.
Assim, teríamos 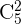 , do qual temos que subtrair dos dados que determinam
, do qual temos que subtrair dos dados que determinam  retas
retas
que não são diagonais.
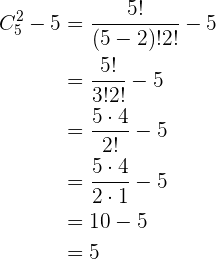
O número anterior não deu o número de diagonais dentro do pentágono. Agora, cada três diagonais quaisquer definem um triângulo dentro do pentágono, ainda que nem sempre o lado do triângulo será toda a diagonal, pois às vezes será apenas parte desta. Isso podemos ver no gráfico de qualquer pentágono com suas diagonais. Podemos ver que, não importa quais diagonais utilizemos, entre estas será formado um triângulo, ainda que este esteja definido apenas por uma parte das diagonais. Dito isso, então cada triângulo é definido por  das
das  diagonais. Assim, obtemos novamente combinações, já que
diagonais. Assim, obtemos novamente combinações, já que
Não entram todos os elementos. Isso porque uma reta é definida apenas por  das
das  diagonais.
diagonais.
Não importa a ordem. Um triângulo está definido por  diagonais, não importa a ordem em que estejam.
diagonais, não importa a ordem em que estejam.
Não repetem-se os elementos. Isso porque os três lados de um triângulo sempre são segmentos de retas diferentes.
Assim, teríamos  .
.
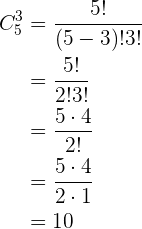
Combinações com condições
Um grupo composto por cinco homens e sete mulheres formam um comitê de 2 homens e 3 mulheres. De quantas maneiras pode ser formado este comitê, se:
1) Pode ser composto por qualquer homem ou mulher.
2) Uma mulher específica deve pertencer ao comitê.
3) Dois homens específicos não podem estar no comitê.
Um grupo composto por cinco homens e sete mulheres formam um comitê de 2 homens e 3 mulheres. De quantas maneiras pode ser formado este comitê, se:
1) Pode ser composto por qualquer homem ou mulher.
Podemos observar que, como podemos escolher qualquer homem, então podemos escolher  dos
dos  homens, não importando quais. Podemos notar que da mesma maneira se cumprem as condições do exercício 1:
homens, não importando quais. Podemos notar que da mesma maneira se cumprem as condições do exercício 1:
Não entram todos os elementos. Isso porque vamos escolher apenas  dos
dos  homens.
homens.
Não importa a ordem. Isso porque dá no mesmo escolher João e Pedro ou Pedro e João.
Não repetem-se os elementos. Isso porque obviamente não podemos escolher mais de uma vez uma pessoa.
Isso nos daria combinações de 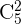 para poder escolher os dois homens. Do mesmo modo, podemos escolher entre todas as mulheres e, além disso, cumprem-se as mesmas condições, portanto, as combinações
para poder escolher os dois homens. Do mesmo modo, podemos escolher entre todas as mulheres e, além disso, cumprem-se as mesmas condições, portanto, as combinações 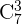 seriam formas diferentes de escolher
seriam formas diferentes de escolher  das
das  mulheres. Isso nos dá como resultado final o produto das combinações que obtemos. Isso é
mulheres. Isso nos dá como resultado final o produto das combinações que obtemos. Isso é
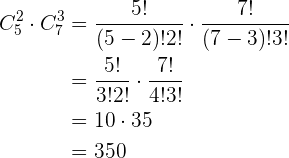
2) Uma mulher específica deve pertencer ao comitê.
Podemos observar que, igual que no enunciado anterior, podemos escolher entre todos os homens, portanto, novamente, teríamos combinações 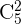 para os homens. Agora, diferente do enunciado anterior com as mulheres, aqui nos dizem que uma mulher específica já está escolhida, portanto, agora devemos escolher as
para os homens. Agora, diferente do enunciado anterior com as mulheres, aqui nos dizem que uma mulher específica já está escolhida, portanto, agora devemos escolher as  que faltam entre as
que faltam entre as  restantes. Isso calculamos com as combinações
restantes. Isso calculamos com as combinações  . Assim, novamente, nosso resultado final é o produto das combinações obtidas:
. Assim, novamente, nosso resultado final é o produto das combinações obtidas:
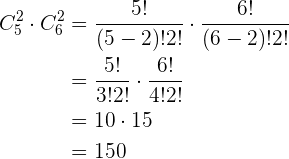
3) Dois homens específicos não podem estar no comitê.
Podemos observar que igual que no enunciado 1, podemos escolher entre todas as mulheres, portanto, novamente, teríamos combinações 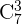 para as mulheres. Agora, diferente dos enunciados anteriores, aqui nos dizem que dois homens dos
para as mulheres. Agora, diferente dos enunciados anteriores, aqui nos dizem que dois homens dos  não podem ser escolhidos, portanto, temos que escolher
não podem ser escolhidos, portanto, temos que escolher  entre os
entre os  restantes. Isso calculamos com as combinações
restantes. Isso calculamos com as combinações 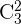 . Por último, nosso resultado final está dado pelo produto das combinações obtidas
. Por último, nosso resultado final está dado pelo produto das combinações obtidas
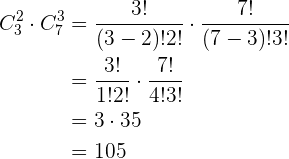
Combinações com moedas
Uma pessoa tem cinco moedas de diferentes valores.
Quantas somas diferentes de dinheiro podemos formar com as cinco moedas?
Uma pessoa tem cinco moedas de diferentes valores.
Quantas somas diferentes de dinheiro podemos formar com as cinco moedas?
Podemos observar que é uma pergunta um pouco duvidosa. Aqui é pedido para calcularmos as diferentes somas, das quais poderíamos nos equivocar em calcular quando usamos todas as moedas (as cinco moedas). No entanto, o que devemos considerar, são as diferentes somas, quando pegamos só uma moeda, quando pegamos duas moedas, três moedas, quatro moedas e cinco moedas, cujas diferentes somas estão dadas por 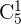 ,
, 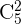 ,
,  ,
, 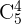 e
e  , respectivamente. Isso é, devemos somar as diferentes maneiras de formar grupos de uma moeda, de duas moedas, de três moedas, e assim, sucessivamente.
, respectivamente. Isso é, devemos somar as diferentes maneiras de formar grupos de uma moeda, de duas moedas, de três moedas, e assim, sucessivamente.
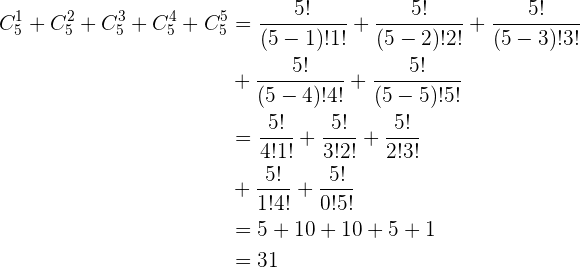
Equações com combinações
Resolva as seguintes equações com combinações:
Resolva as seguintes equações com combinações:
Resolveremos utilizando simplesmente as definições de variações e de combinações
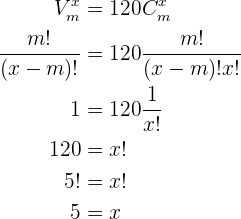
Portanto  .
.
2. 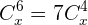
Novamente utilizaremos a definição de combinações para resolver este problema
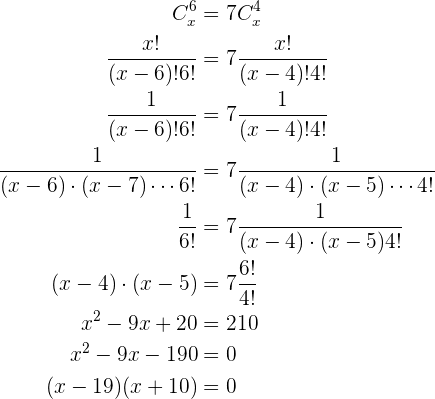
Com o anterior, compreendemos que 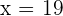 ou
ou 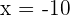 , no entanto, como
, no entanto, como  deve ser obrigatoriamente positivo, nossa única opção é
deve ser obrigatoriamente positivo, nossa única opção é 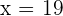 .
.
3. 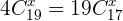
Novamente, utilizaremos a definição de combinações para resolver este problema
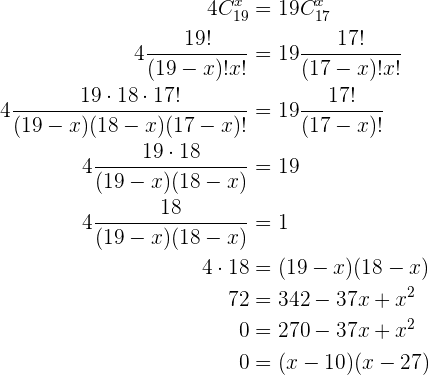
Com o anterior, compreendemos que 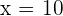 ou
ou 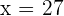 , no entanto, como
, no entanto, como  deve ser obrigatoriamente menor que
deve ser obrigatoriamente menor que  e
e  , já que não podemos pegar mais elementos dos que já existem no conjunto, nossa única opção é
, já que não podemos pegar mais elementos dos que já existem no conjunto, nossa única opção é 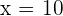 .
.
Resumir com IA:













