Encontre a probabilidade de que ao lançarmos duas moedas no ar, saiam:
- Duas caras
- Duas coroas
- Uma cara e uma coroa
Encontre a probabilidade de que ao lançarmos duas moedas no ar, saiam:
a) Duas caras.
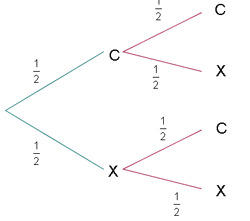
Multiplicamos a probabilidade de sucesso de que saia uma cara em uma moeda (1/2), pela probabilidade de sucesso na outra moeda (1/2), já que são probabilidades independentes:
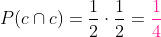
b) Duas coroas.
A chance de que saia uma coroa em uma moeda e também coroa na outra são probabilidades independentes e cada uma tem uma probabilidade de (1/2), como observamos no esquema. Por essa razão, multiplicamos ambas probabilidades:
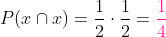
c) Uma cara e uma coroa.
A probabilidade de tirar uma cara e uma coroa se refere a duas possibilidades: cara e coroa ou coroa e cara. Isso significa que primeiro devemos tirar a probabilidade de cada opção (1/2) (1/2) e depois somá-las para obter o resultado. Observe:
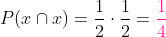
Encontre a probabilidade de que, ao levantarmos nossas fichas de dominó, obtemos um número de pontos maior do que 9 ou que seja múltiplo de 4.
Encontre a probabilidade de que, ao levantarmos nossas fichas de dominó, obtemos um número de pontos maior do que 9 ou que seja múltiplo de 4.
No conjunto A colocamos as fichas cujo o total de pontos de cada uma é maior do que nove e no conjunto B as fichas cujo a quantidade de pontos de cada uma é múltiplo de quatro:
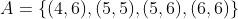
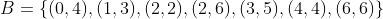
Neste caso observamos que a ficha (6, 6) pertence a ambos conjuntos. Em outras palavras: 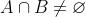
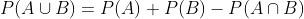
Agora, levando em conta que existem 28 fichas de dominó, os valores ficam da seguinte forma:
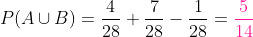
Um dado está viciado, de forma que as chances de obtermos os diferentes lados são proporcionais aos números destes. Encontre:
- A probabilidade de obtermos o 6 em um lançamento
- A probabilidade de conseguirmos um número ímpar em um lançamento
Um dado está viciado, de forma que as chances de obtermos os diferentes lados são proporcionais aos números destes. Encontre:
a) A probabilidade de obtermos o 6 em um lançamento
Já que o dado está viciado, a probabilidade de cada lado é proporcional ao número de lados correspondentes.
Por exemplo: 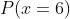
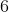
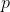
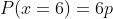
e assim com os demais lados.
Se por outro lado, somamos as probabilidades de cada lado, teremos:
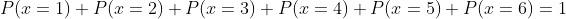
e então:
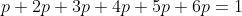
assim, portanto:
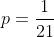
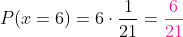
b) A probabilidade de conseguir um número ímpar em um lançamento
Neste caso, basta somar as probabilidades de conseguir todos os ímpares possíveis.
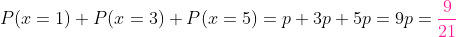
Dois dados são lançados ao ar e a soma dos pontos obtidos anotados. Pede-se:
- A probabilidade de que saia o 7
- A probabilidade de que o número obtido seja par
- A probabilidade de que o número obtido seja múltiplo de três
Dois dados são lançados ao ar e a soma dos pontos obtidos anotados. Pede-se:
a) A probabilidade de que saia o 7
Agrupamos todas as possibilidades onde a soma seja sete:

nos damos conta de que são possíveis 6 formas e como há 36 diferentes formas das quais os dois dados podem cair, então:
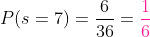
b) A probabilidade de que o número obtido seja par
Os pares para que o número obtido seja par são
(1,1)
(1,3), (2,2),(3,1)
(1,5),(2,4),(3,3),(4,2),(5,1)
(2,6),(3,5),(4,4),(5,3),(6,2)
(4,6),(5,5),(6,4)
(6,6)
um total de 18. Isso significa que a probabilidade de que o resultado obtido seja par é:
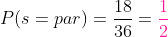
c) A probabilidade de que o número obtido seja múltiplo de três
Nos damos conta de que cada um dos pares somam algum múltiplo de três:
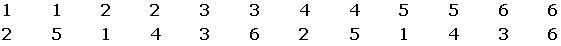
um total de 12. Então:
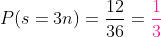
que representa os múltiplos de 3.
São lançados três dados. Encontre a probabilidade de que :
- Saia 6 em todos
- Os pontos obtidos somem 7
São lançados três dados. Encontre a probabilidade de que:
a) Saia 6 em todos
Existe apenas uma forma de que saia seis em todos (6, 6, 6) e se consideramos que há 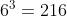
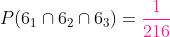
b) Os pontos obtidos somem 7
Aqui se encontram as formas das quais podem cair os dados, cuja soma dos pontos é sete:
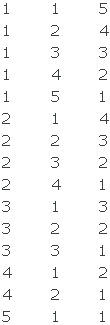
e com esta lista, nos damos conta de que existem 15 formas diferentes para que a soma seja 7. Então a probabilidade desejada é de:
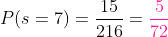
Encontre a probabilidade de que ao jogar um dado ao ar, saia:
- Um número par
- Um múltiplo de três
- Maior que quatro
Encontre a probabilidade de que ao jogar um dado ao ar, saia:
a) Um número par
Para que seja par, existem as seguintes opções: 2, 4, 6.
Isso significa que há 3 formas das 6 possíveis. Dessa maneira a probabilidade é de:
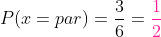
b) Um múltiplo de três
Neste caso os múltiplos de três são: 3 e 6. Portanto há 2 formas de que seja múltiplo de 3 e 6 formas em que pode cair um dado
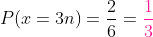
c) Maior que quatro
Neste caso, os maiores que quatro são 5 e 6. Assim, a probabilidade é de:
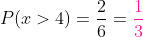
São retiradas duas bolas de uma urna que está composta de uma bola branca, uma vermelha, uma verde e uma preta. Descreva o espaço amostral quando:
- A primeira bola volta para a urna antes de se retirar a segunda
- A primeira bola não volta para a urna
São retiradas duas bolas de uma urna que está composta de uma bola branca, uma roxa, uma verde e uma neon. Descreva o espaço amostral quando:
a) A primeira bola volta para a urna antes de se retirar a segunda
A primeira bola pode ser qualquer uma das quatro B, R, V, N. No momento de registrar a que saiu e colocá-la de volta na urna, pode sair novamente qualquer uma das quatro. Isso significa que por exemplo se em um primeiro momento saiu B, então na segunda extração pode sair BB, BR, BV ou BN, e assim sucessivamente com as demais opções. Assim, nosso espaço amostral é
E = {BB, BR, BV, BN, RB, RR, RV, RN, VB, VR, VV, VN, NB, NR, NV, NN}
b) A primeira bola não volta para a urna
Como a bola que retiramos no início não volta para a urna, então na segunda extração deve sair alguma das quatro restantes. Isso significa que já não é possível que se repita a bola. Assim, nosso espaço amostral é
E = { BR, BV, BN, RB, RV, RN, VB, VR, VN, NB, NR, NV}
Uma urna tem oito bolas vermelhas cinco amarelas e sete verdes. Se retiramos uma ao acaso, qual é a chance de que:
- Seja vermelha
- Seja verde
- Seja amarela
- Não seja vermelha
- Não seja amarela
Uma urna tem oito bolas vermelhas, cinco amarelas e sete verdes. Se retiramos uma ao acaso, qual é a chance de que:
a) Seja vermelha
De um total de 20 bolas, há 8 bolas vermelhas. Então, a probabilidade é de:
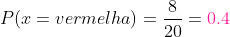
b) Seja verde
Como há 7 bolas verdes a probabilidade é de:
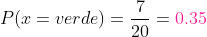
c) Seja amarela
De um total de 20 bolas, 5 são amarelas. Então:
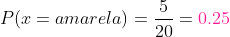
d) Não seja vermelha
Já que devemos calcular a probabilidade de que NÃO seja uma bola vermelha, então podemos subtrair do total (1) a probabilidade de que SIM seja vermelha. Assim, a probabilidade é de:
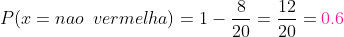
e) Não seja amarela
Aqui utilizamos o mesmo princípio do enunciado anterior:
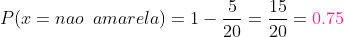
Uma urna contém três bolas vermelhas e sete brancas. Extraímos duas bolas ao acaso. Escreva o espaço amostral e encontre a probabilidade de:
- Extrair as duas bolas com substituição
- Sem substituição
Uma urna contém três bolas vermelhas e sete brancas. Extraímos duas bolas ao acaso. Escreva o espaço amostral e encontre a probabilidade de:
a) Extrair as duas bolas com substituição
Primeiro descrevemos o espaço amostral. Já que existem dois tipos de bolas, vermelhas (V) ou brancas (B), na nossa primeira extração podemos retirar qualquer uma das duas bolas. E como a quantidade de cada uma delas é maior do que um, então (com substituição ou sem substituição) na segunda extração, também podemos obter qualquer uma das duas. Assim, o espaço amostral é o seguinte:
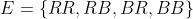
Agora, ao extrairmos uma bola e depois colocá-la de volta na urna (substituí-la), as condições da primeira e da segunda extração são exatamente iguais. Isso significa que são chances independentes. Aqui podemos aplicar a seguinte fórmula que funciona para chances independentes:
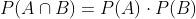
Primeira extração R, segunda R:
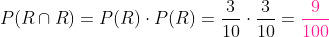
Primeira extração R, segunda B:
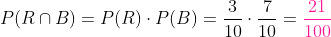
Primeira extração B, segunda R:
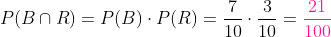
Primeira extração B, segunda B:
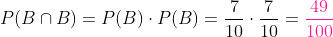
b) Sem substituição
Neste caso, como há substituição, a extração da primeira bola modifica as condições da segunda extração. Por exemplo, se na primeira extração obtemos uma bola vermelha, isso significa que na segunda extração há uma bola vermelha a menos na urna, ou seja, 2 bolas vermelhas. Além disso, uma bola a menos do total, ou seja, 9. Isso significa que são chances dependentes.
Vejamos todas as opções.
Primeira extração R, segunda R:
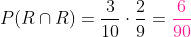
Primeira extração R, segunda B:
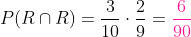
Primeira extração B, segunda R:
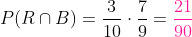
Primeira extração B, segunda B:
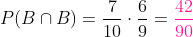
Extraímos uma bola de uma urna que contém 4 bolas vermelhas, 5 brancas e 6 pretas
- Qual a probabilidade de que a bola seja vermelha ou branca?
- Qual a probabilidade de que não seja branca?
Extraímos uma bola de uma urna que contém 4 bolas vermelhas, 5 brancas e 6 pretas
a) Qual a probabilidade de que a bola seja vermelha ou branca?
b) Qual a probabilidade de que não seja branca?
Aqui, tratam-se de chances onde não há elementos em comum. Desse modo, da fórmula:
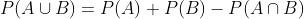
apenas ficamos com:
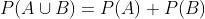
dessa maneira, a probabilidade de que a bola seja vermelha ou branca é de:
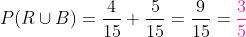
e a probabilidade de que a bola NÃO seja branca é de:
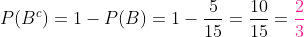
Em uma classe há 10 alunas loiras, 20 morenas, 5 alunos loiros e 10 morenos. Em um dia de aula qualquer, há 44 alunos. Encontre a probabilidade de que o aluno que faltou:
- Seja homem
- Seja uma mulher morena
- Seja homem ou mulher
Em uma classe há 10 alunas loiras, 20 morenas, 5 alunos loiros e 10 morenos. Em um dia de aula qualquer, há 44 alunos. Encontre a probabilidade de que o aluno que faltou:
a) Seja homem
Na seguinte tabela, temos a informação para o problema:
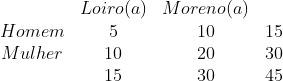
daqui podemos ver que há 15 homens e 45 alunos. Então, a probabilidade de que seja homem é de:
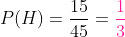
b) Seja uma mulher morena
Há 20 mulheres morenas, então:
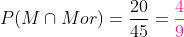
c) Seja homem ou mulher
Aqui a probabilidade é o total:
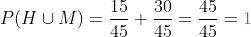
Em um envelope há 20 folhas. Oito delas têm um desenho de um carro e as restantes estão em branco. Encontre a probabilidade de extrairmos ao menos uma folha com o desenho de um carro:
- Se retirarmos uma folha
- Se retirarmos duas folhas
- Se retirarmos três folhas
Em um envelope há 20 folhas. Oito delas têm um desenho de um carro e as restantes estão em branco. Encontre a probabilidade de extrairmos ao menos uma folha com o desenho de um carro:
a) A Se retirarmos uma folha
Como há 8 folhas com o desenho de um carro e 20 folhas no total, a probabilidade de extrairmos uma folha com o desenho de um carro é de:
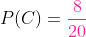
b) Se retirarmos duas folhas
Ao extrairmos duas folhas, podem sair BB, CB, BC ou CC. Poderíamos tirar a probabilidade de CB, BC, CC e depois somá-las. No entanto é mais prático calcular a probabilidade de BB e subtrair 1 do valor obtido:
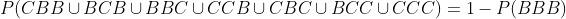
c) Se retirarmos três folhas
Aqui podemos nos basear na mesma dedução do enunciado anterior:
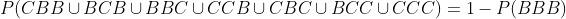
Então:
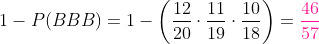
Os estudantes A e B têm respectivamente a probabilidade 1/2 e 1/5 de reprovarem em um exame. A probabilidade de que sejam simultaneamente reprovados no exame é de 1/10. Determine a probabilidade de que ao menos um dos estudantes seja reprovado no exame.
Os estudantes A e B têm respectivamente a probabilidade 1/2 e 1/5 de reprovarem em um exame. A probabilidade de que sejam simultaneamente reprovados no exame é de 1/10. Determine a probabilidade de que ao menos um dos estudantes seja reprovado no exame.
São chances compatíveis, ou seja, a probabilidade de eventos simultâneos é diferente de zero. Calculamos então a probabilidade da seguinte maneira:
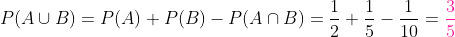
Dois irmãos saem para caçar. O primeiro mata em média 2 alvos a cada 5 disparos e o segundo 1 alvo a cada 2 disparos. Se os dois disparam ao mesmo tempo um mesmo alvo, qual é a probabilidade de que o mate?
Dois irmãos saem para caçar. O primeiro mata em média 2 alvos a cada 5 disparos e o segundo 1 alvo a cada 2 disparos. Se os dois disparam ao mesmo tempo um mesmo alvo, qual é a probabilidade de que o mate?
A probabilidade de que o primeiro irmão mate um alvo é de:
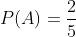
a probabilidade de que o segundo irmão mate um alvo é de:
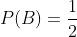
por outro lado a probabilidade de que ambos matem ao mesmo tempo um alvo é de:
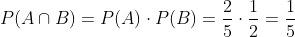
então, se eles disparam ao mesmo tempo, no mesmo alvo, seja o irmão A ou o irmão B, a chance de matarem o alvo é de:
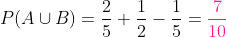
Uma turma é composta por 10 homens e 20 mulheres. A metade dos homens e a metade das mulheres tem olhos castanhos. Determine a probabilidade de que uma da pessoa escolhida ao acaso seja um homem ou tenha os olhos castanhos.
Uma turma é composta formada de 10 homens e 20 mulheres. A metade dos homens e a metade das mulheres tem olhos castanhos. Determine a probabilidade de que uma da pessoa escolhida ao acaso seja um homem ou tenha os olhos castanhos.

Aqui devemos observar que há tanto homens (10) como de olhos castanhos (15). Além de homens com olhos castanhos (5). Desse modo, a probabilidade de que seja homem ou tenha olhos castanhos é calculada com a fórmula:
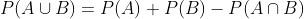
fazemos o cálculo:
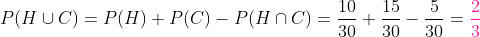
A probabilidade de que um homem viva 20 anos é de 1/4 e a de que sua mulher viva 20 anos é de 1/3. Pede-se para calcular a probabilidade:
- De que ambos vivam 20 anos.
- De que o homem viva 20 anos e sua mulher não.
- De que ambos morram antes dos 20 anos.
A probabilidade de que um homem viva 20 anos é de 1/4 e a de que sua mulher viva 20 anos é de 1/3. Pede-se para calcular a probabilidade:
a) De que ambos vivam 20 anos
O que ocorrer com um não afetará o outro. Por essa razão, são chances independentes. Assim, podemos calcular a probabilidade da seguinte maneira:
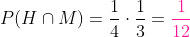
b) De que o homem viva 20 anos e sua mulher não
Aqui também são chances independentes, então podemos tratar como tal. Apenas utilizamos a fórmula que calcula a probabilidade de que NÃO ocorra algo:
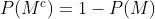
então:
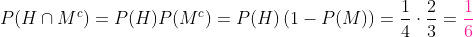
c) De que ambos morram antes dos 20 anos
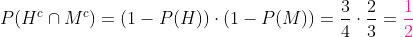
Calcule a probabilidade de tirar exatamente duas coroas ao jogar uma moeda quatro vezes.
Calcule a probabilidade de tirar exatamente duas coroas ao jogar uma moeda quatro vezes
Os resultados possíveis para cada lançamento são cara (C) ou coroa (X).
Primeiro podemos encontrar as maneiras em que podem sair duas coroas (X) em quatro lançamentos.
De quatro resultados possíveis n=4, vejamos de quantas maneiras r=2 eles são iguais. Ou seja, calculamos o total de grupos de dois elementos (resultados iguais) que podemos extrair de um total de quatro elementos (resultados possíveis).
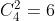
como vimos são 6. Com a finalidade de sermos mais claros, aqui mostramos as 6 maneiras
XXCC, XCXC, XCCX, CXXC, CXCX, CCXX
por fim, o total de maneiras em que as moedas podem sair ao serem lançadas quatro vezes, levando em conta que são duas opções para cada uma, é de 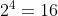
Portanto, a probabilidade de tirar exatamente duas coroas ao acaso ao jogarmos uma moeda quatro vezes é de:
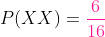
Um grupo de 10 pessoas se sentam em um banco. Qual é a probabilidade de que duas pessoas que já estavam sentadas anteriormente se sentem juntas.
Um grupo de 10 pessoas se sentam em um banco. Qual é a probabilidade de que duas pessoas que já estavam sentadas anteriormente se sentem juntas
Para conhecer todas as maneiras em que devem ser colocadas 10 pessoas em 10 lugares, usaremos a permutação:
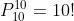
Agora, para saber o total de maneiras em que duas pessoas selecionadas previamente se sentem juntas, podemos pensar que ao se sentarem juntas ocupam um lugar entre nove possibilidades. Desse modo, as maneiras em que nove pessoas podem se sentar ocupando nove lugares é:
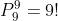
E o fato de que quando se sentam juntas possa ocorrer de duas maneiras possíveis: ab ou ba, então o total de maneiras em que duas pessoas selecionadas previamente possam se sentar juntas em 10 lugares possíveis é 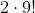
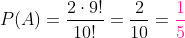
Extraímos cinco cartas de um baralho de 52 cartas. Encontre a probabilidade de extrairmos:
- 4 ases
- 4 ases e um rei
- 3 cincos e 2 valetes
- Um 9, 10, valete, cavaleiro e rei em qualquer ordem
- 3 de paus e 2 de outro
- Ao menos um às.
Extraímos cinco cartas de um baralho de 52 cartas. Encontre a probabilidade de extrairmos:
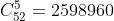
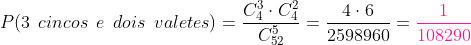
a) 4 ases
Primeiro, o total de maneiras em que podemos combinar 52 cartas, ao agrupá-las de 5 em 5, são:
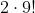
Agora, de 4 ases formamos um grupo (sem importar a ordem) de 4, sob a fórmula 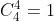
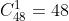
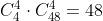
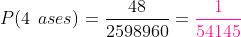
b) 4 ases e um rei
Para 4 ases existe apenas uma possibilidade, e para que obtemos um rei há quatro possibilidades. Em outras palavras, multiplicamos as possibilidades de 4 ases pelas do rei: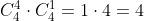
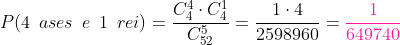
c) 3 cincos e 2 valetes
Há 4 cincos e destes queremos 3. Por outro lado, há 4 valetes e destes queremos 2. Então,
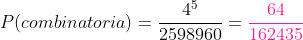
d) Um 9, 10, valete, cavaleiro e rei em qualquer ordem
Para cada carta há 4 possibilidades e como são 5 cartas, então temos 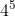
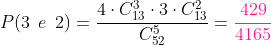
e) 3 de paus e 2 de outro
Para que tenhamos 3 de paus de um naipe (13 cartas), então calculamos e como são 4 paus, então 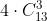
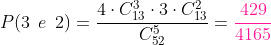
f) Ao menos um ás
Primeiro calculamos a probabilidade de que NÃO saia ás. Isso significa que vamos tirar todos os ases:
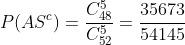
E então, a probabilidade de que saia ao menos um ás, é o restante:
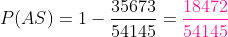
Resumir com IA:


