Definição de assíntotas
As assíntotas são retas às quais a função se aproxima indefinidamente.
Existem três tipos de assíntotas:
1Horizontais
2Verticais
3Oblíquas
Assíntotas horizontais
Se uma das seguintes condições for satisfeita:
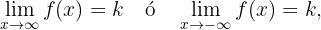
então a reta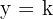 
é uma assíntota horizontal do gráfico da função 
Exemplo: Calcule as assíntotas horizontais da função:
Calculamos o limite quando 
tende a 
. Para isso, dividimos cada termo do numerador e do denominador por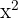 
:
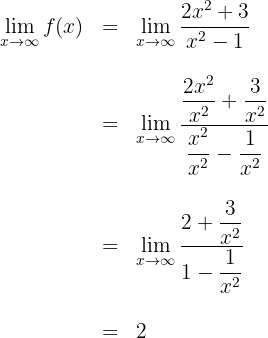
Assim, a função possui uma assíntota horizontal em: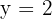 
Assíntotas verticais
Se uma das seguintes condições for satisfeita:
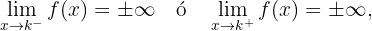
então a reta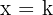 
é uma assíntota vertical do gráfico da função
Observe que 
são os valores que não pertencem ao domínio da função (no caso de funções racionais).
Exemplo: Calcule as assíntotas verticais da função.
O domínio da função é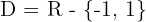 
Calculamos os limites laterais quando tende a 
Portanto, a função possui uma assíntota vertical em
Calculamos os limites laterais quando tende para 
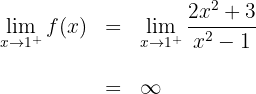
Portanto, a função possui outra assíntota vertical em 
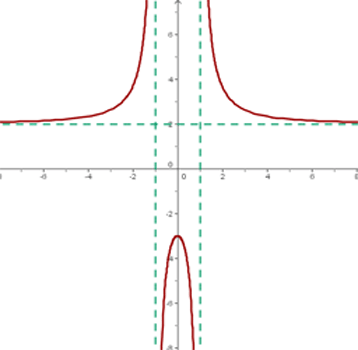
Esses comportamentos podem ser visualizados no gráfico da função.
Assíntotas oblíquas
Só buscamos assíntotas oblíquas quando não existem assíntotas horizontais.
Para que exista uma assíntota oblíqua, é necessário que o grau do numerador seja exatamente um grau maior que o grau do denominador. Nesse caso, a assíntota é dada por:
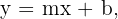
onde:
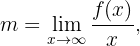
Exemplo: Calcule as assíntotas da função:
O grau do numerador é exatamente um a mais que o grau do denominador. Só falta verificar se existem assíntotas horizontais.
Calculamos o limite quando pende para , . Para isso, dividimos todos os termos por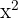
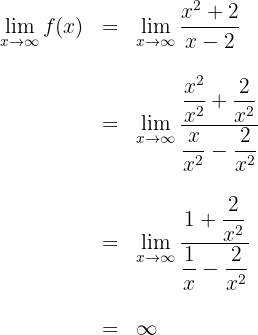
Portanto, a função não possui assíntotas horizontais.
Agora, verificamos se há assíntotas oblíquas, calculando:
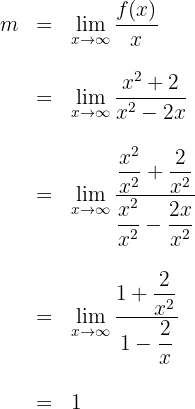
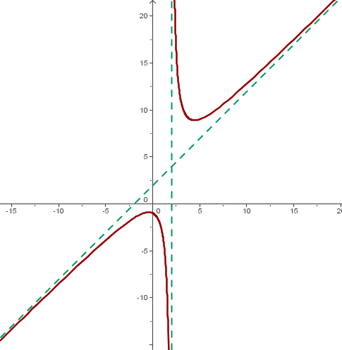
Portanto, a assíntota oblíqua é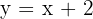 
Note que o domínio da função é
e que 
é uma assíntota vertical.
Gostou desse artigo? Deixe uma nota!
Loading...
