Temas

O que são equações lineares?
As equações lineares ou do primeiro grau são do tipo 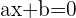 , com
, com  , ou qualquer outra equação da qual ao operarmos, trocarmos ou simplificarmos, adquiram essa expressão.
, ou qualquer outra equação da qual ao operarmos, trocarmos ou simplificarmos, adquiram essa expressão.
Passos para resolver uma equação linear
De maneira geral para resolver uma equação linear ou de primeiro grau devemos seguir os seguintes passos:
Retiramos os parênteses
Isto é, se há expressões como

Então desenvolvemos o cálculo, levando em conta a propriedade distributiva, isto é  e também a lei dos sinais será importante.
e também a lei dos sinais será importante.

Retiramos os denominadores
No caso em que existam termos fracionários na expressão, devemos identificar os diferentes denominadores que há, calcular o mínimo múltiplo comum (mmc) deles e multiplicar a equação pelo mmc. Ou em vez do mmc, também podemos calcular o produto de todos os denominadores, ainda que seja recomendado o primeiro procedimento, pois é um número menor ou mais simplificado. Por exemplo:
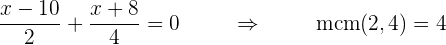
multiplicamos a primeira fração por 

Aqui, novamente, poderíamos ter que retirar os parênteses para simplificar

Agrupamos os termos com x em um membro e os termos independentes em outro
Já que fizemos o passo 1 e o passo 2, temos a soma e a subtração dos termos com x e os termos independentes de ambos os lados da equação, em seguida basta juntar os  de um lado e os termos independentes do outro. Para isso, lembre-se que se de um lado da equação estamos somando um
de um lado e os termos independentes do outro. Para isso, lembre-se que se de um lado da equação estamos somando um  , por exemplo, podemos passá-lo para o outro lado com uma operação inversa, assim, ficaria como
, por exemplo, podemos passá-lo para o outro lado com uma operação inversa, assim, ficaria como  do outro lado
do outro lado

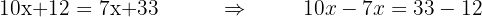
Reduzimos o termos semelhantes
Já que temos termos com  juntos, podemos somá-los ou diminuí-los, isso dependerá. Do mesmo modo com os termos independentes, por exemplo:
juntos, podemos somá-los ou diminuí-los, isso dependerá. Do mesmo modo com os termos independentes, por exemplo:

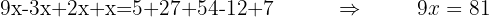
Isolamos a incógnita
Se há um coeficiente acompanhando a variável  , como ele está multiplicando, passamos ele para o outro lado com uma operação inversa, isto é, dividindo. Chamaremos isso de isolar
, como ele está multiplicando, passamos ele para o outro lado com uma operação inversa, isto é, dividindo. Chamaremos isso de isolar
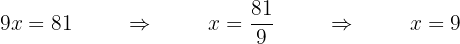
Exercícios de equações lineares
 .
.

Isolamos a incógnita:



Agrupamos os termos semelhantes e os independentes e somamos:



Retiramos os parênteses: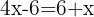
Agrupamos os termos e somamos:

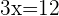
Isolamos a incógnita:
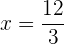
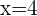


Retiramos os denominadores, para isso, em primeiro lugar, encontramos o mínimo múltiplo comum.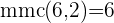
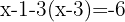
Retiramos os parênteses, agrupamos e somamos os termos semelhantes:
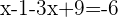
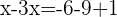
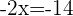
Isolamos a incógnita:
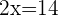
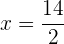

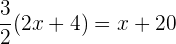
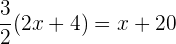
Retiramos parênteses e simplificamos
Retiramos os denominadores, agrupamos e somamos os termos semelhantes
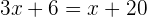
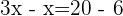
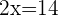

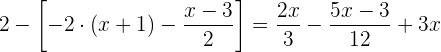
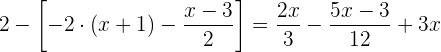
Retiramos o colchete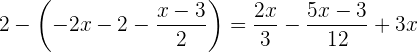
Retiramos os parênteses
Retiramos os denominadores
Retiramos os parênteses
Agrupamos os termos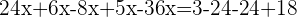
Somamos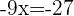
Dividimos os dois membros por 
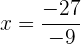



Retiramos os parênteses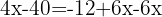
Agrupamos os termos com a variável x de um lado da equação e os independentes do outro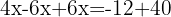
Somamos os termos semelhantes para simplificar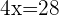
Dividimos a equação entre 




Retiramos os parênteses
Agrupamos os termos com a variável x de um lado da equação e os independentes do outro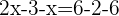
Somamos os termos semelhantes para simplificar
Dividimos entre 




Procuramos o mmc dos denominadores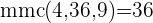
Multiplicamos a equação por 
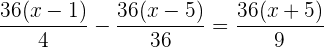
Simplificamos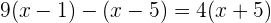
Retiramos os parênteses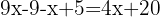
Agrupamos os termos com a variável  de um lado da equação e os independentes do outro
de um lado da equação e os independentes do outro
Somamos os termos semelhantes para simplificar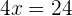
Dividimos entre 
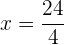
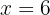


Retiramos os parênteses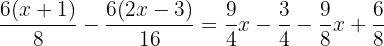
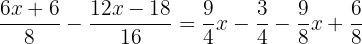
Procuramos o mmc dos denominadores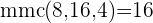
Multiplicamos a equação por 

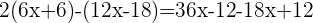
Retiramos os parênteses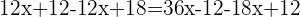
agrupamos os termos semelhantes e somamos

Dividimos entre  toda a equação e isolamos
toda a equação e isolamos 

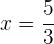
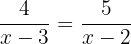
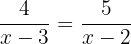
Multiplicamos toda a equação pelo produto dos denominadores, isto é, por 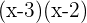

Simplificamos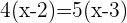
Retiramos os parênteses
Agrupamos os termos semelhantes e somamos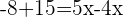

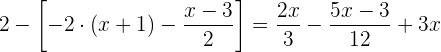
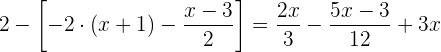
Retiramos os parênteses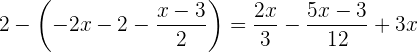

Encontramos o mmc dos denominadores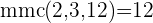
Multiplicamos a equação por 
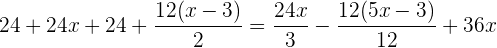

Retiramos os parênteses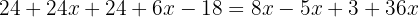
Agrupamos os termos semelhantes e somamos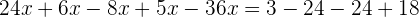

Isolamos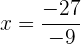

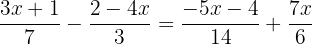
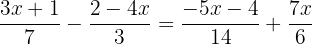
Encontramos o mmc dos denominadores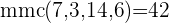
Multiplicamos por 
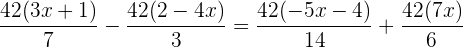
Simplificamos calculando quanto é  entre o respectivo denominador para obter o coeficiente, por exemplo
entre o respectivo denominador para obter o coeficiente, por exemplo
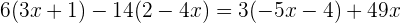
Retiramos os parênteses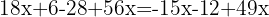
Agrupamos os termos semelhantes e somamos
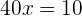
Dividimos entre  e isolamos
e isolamos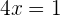
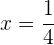
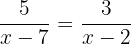
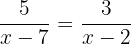
Multiplicamos toda a equação pelo produto dos denominadores, isto é, por 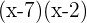

Simplificamos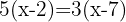
Retiramos os parênteses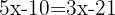
Agrupamos os termos semelhantes e somamos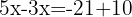
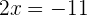
Isolamos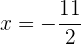
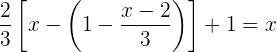
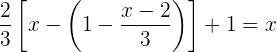
Retiramos os parênteses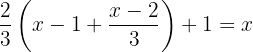
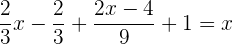
Calculamos o mmc dos denominadores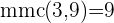
Multiplicamos a equação por 
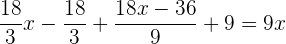
Simplificamos
Agrupamos os termos semelhantes e multiplicamos por 


Resumir com IA:












