Definição de função inversa
É chamada de função inversa ou recíproca de 
a outra função 
que satisfaz :
Se 
, então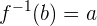 
Vamos ver um exemplo a partir da função 
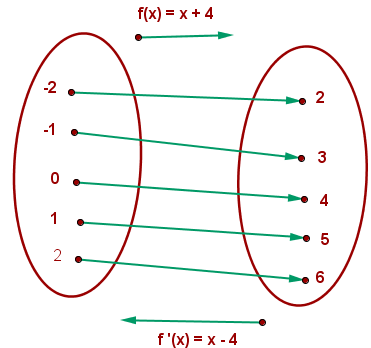
Podemos observar que:
- O domínio de é o alcance de .
- O alcance de é o domínio de .
Se queremos encontrar o alcance de uma função temos que encontrar o domínio de sua função inversa.
Se duas funções são inversas sua composição é a função identidade.
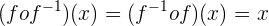
Os gráficos de e são simétricas em relação à bissetriz do primeiro e terceiro quadrante."
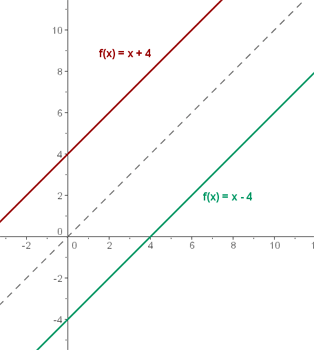
Deve-se distinguir entre a função inversa, , e a inversa de uma função: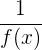 
.
A inversa da função é
.
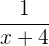A função inversa de é 
porque a combinação das duas funções é a função identidade
Cálculo da função inversa
Para construir ou calcular a função inversa de qualquer função, é necessário seguir os passos a seguir:
Passo 1: A função é escrita com 
e 
.
Passo 2: A variável é isolada em função da variável .
Passo 3:As variáveis são trocadas
Exemplos com exercícios resolvidos
Calcular a função inversa de:
1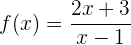 
Trocamos por
Removemos os denominadores
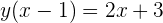
Resolvemos o parênteses
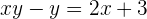
Transferimos para o primeiro membro como
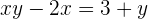
Extraímos o fator comum, ou seja, o
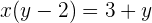
Agora, isolamos o
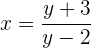
Trocamos x por e obteremos a função inversa
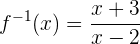
Vamos verificar o resultado para 
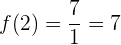
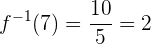
Como 
resulta em 
e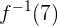 
resulta em 
, isso quer dizer que a função inversa está certa.
2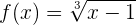 
Trocamos por
Elevamos ao cubo em ambos os lados
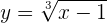
Isolamos e trocamos por
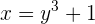
3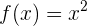 
Trocamos por
Isolamos a
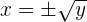
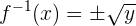
Não se trata de uma função
Não existe função inversa porque qualquer elemento possui duas imagens, e uma função pode ter, no máximo, uma imagem.
Gostou desse artigo? Deixe uma nota!
Loading...
