De um triângulo sabemos que:  ,
,  e
e  . Calcule os elementos restantes.
. Calcule os elementos restantes.
De um triângulo sabemos que:  ,
,  e
e  . Calcule os elementos restantes.
. Calcule os elementos restantes.
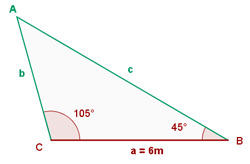
1) Como a soma dos três ângulos de um triângulo é 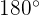 , podemos calcular facilmente o ângulo
, podemos calcular facilmente o ângulo  :
:

2) Aplicamos a lei de senos para calcular os lados  e
e  :
: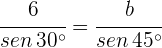
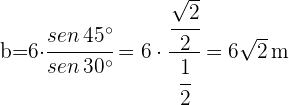
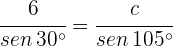

De um triângulo sabemos que:  ,
,  e
e  . Calcule os elementos restantes.
. Calcule os elementos restantes.
De um triângulo sabemos que:  ,
,  y
y  . Calcule os elementos restantes.
. Calcule os elementos restantes.
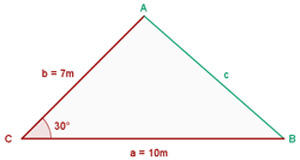
1) Aplicamos a lei de cossenos para calcular o lado  :
:
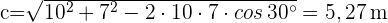
2) Aplicamos a lei de senos para calcular o ângulo  :
: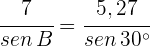
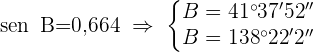
 já que
já que  , o ângulo obtuso será
, o ângulo obtuso será  .
.
3) Para calcular o ângulo  verificamos que somem
verificamos que somem  :
: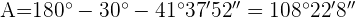
Resolva o triângulo com os seguintes dados: A = 30°, a = 3 m e b = 8 m.
Resolva o triângulo com os seguintes dados: 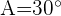 ,
, 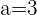 m e
m e 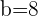 m.
m.
1) Aplicamos a lei de senos com os dados

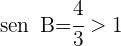
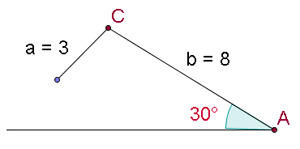
2) Como o seno de um ângulo nunca pode ser maior que  , o problema não tem solução. A figura mostra a impossibilidade de que tal ângulo exista.
, o problema não tem solução. A figura mostra a impossibilidade de que tal ângulo exista.

Resolva o triângulo com os seguintes dados: 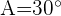 ,
, 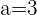 m e
m e 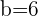 m.
m.
Resolva o triângulo com os seguintes dados: 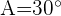 ,
, 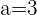 m e
m e 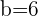 m.
m.
1) Aplicamos a lei de senos para calcular o ângulo  :
:
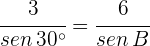
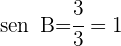
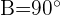
2) Como 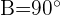 , é um triângulo retângulo, podemos calcular o ângulo
, é um triângulo retângulo, podemos calcular o ângulo  considerando que os ângulos agudos devem somar
considerando que os ângulos agudos devem somar  :
:
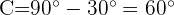
3) Calculamos o lado  aplicando funções trigonométricas:
aplicando funções trigonométricas:

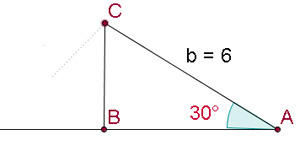
Resolva o triângulo com os seguintes dados: 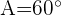 ,
,  m e
m e  m.
m.
Resolva o triângulo com os seguintes dados: 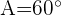 ,
,  m e
m e  m.
m.
1) Aplicamos a lei de senos para calcular o ângulo 

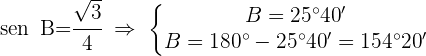
2) Como  , apenas a seguinte solução é válida:
, apenas a seguinte solução é válida: 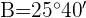
3) Calculamos o ângulo  considerando que os 3 ângulos devem somar
considerando que os 3 ângulos devem somar  :
:
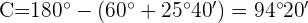
4) Calculamos o lado  aplicando a lei de senos:
aplicando a lei de senos:

 m
m
Resolva o triângulo com os seguintes dados: 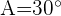 ,
,  e
e 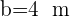 .
.
Resolva o triângulo com os seguintes dados: 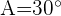 ,
,  e
e 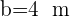 .
.
1) Aplicamos a lei de senos para calcular o ângulo  :
: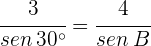
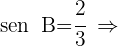

2) Como 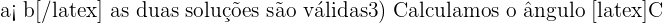 e o lado
e o lado  para o valor de
para o valor de 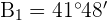
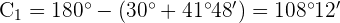

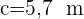
4) Calculamos o ângulo  e o lado
e o lado  para o valor de
para o valor de 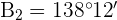
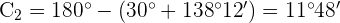
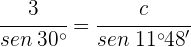
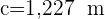
Resolva o triângulo com os seguintes dados:  ,
, 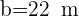 e
e 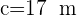 .
.
Resolva o triângulo com os seguintes dados:  ,
, 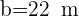 e
e 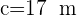 .
.
1) Aplicamos a lei de cossenos para calcular os ângulos  e
e 
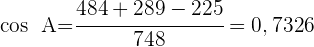
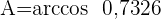
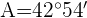
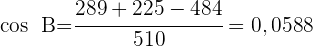
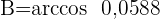

2) Calculamos o ângulo  considerando que os três ângulos somam
considerando que os três ângulos somam

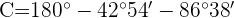
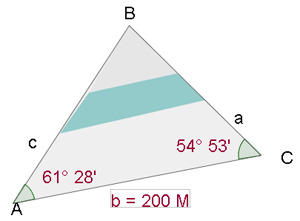
Calcule a altura,  , da figura:
, da figura:
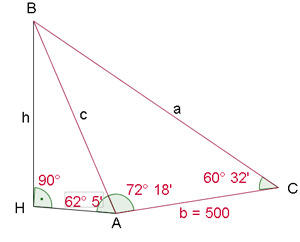
Calcule a altura,  , da figura:
, da figura:

1) Como conhecemos 2 ângulos do triângulo  , podemos calcular o
, podemos calcular o  considerando que a soma dos três ângulos deve ser
considerando que a soma dos três ângulos deve ser 
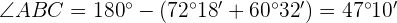
2) Aplicamos a lei de senos para calcular o lado  :
:
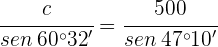
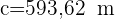
3) Como o triângulo 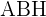 é retângulo, aplicamos funções trigonométricas para calcular o lado
é retângulo, aplicamos funções trigonométricas para calcular o lado  :
:
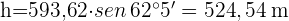
Calcule a distância que separa o ponto  do ponto inacessível
do ponto inacessível  .
.
Calcule a distância que separa o ponto  do ponto inacessível
do ponto inacessível  .
.

1) Calculamos o ângulo  considerando que a soma dos três ângulos é
considerando que a soma dos três ângulos é  :
:
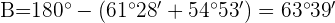
2) Aplicamos a lei de senos para calcular o lado  :
:
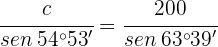
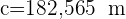
Calcule a distância que separa dois pontos inacessíveis  e
e  .
.
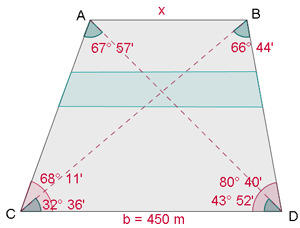
Calcule a distância que separa dois pontos inacessíveis  e
e  .
.

1) Considerando o triângulo 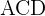 , aplicamos a lei de senos para calcular
, aplicamos a lei de senos para calcular 

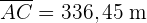
2) Considerando o triângulo 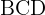 , aplicamos a lei de senos para calcular
, aplicamos a lei de senos para calcular 


3) Aplicamos a lei de cossenos para calcular a distância 


Calcule o raio do círculo circunscrito em um triângulo, onde 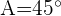 ,
, 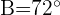 e
e 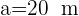 .
.
Calcule o raio do círculo circunscrito em um triângulo, onde 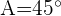 ,
, 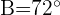 e
e 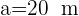 .
.
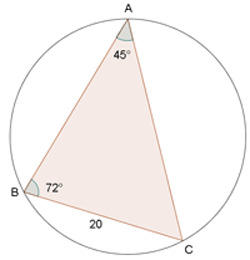
1) Considerando que 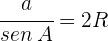

O raio de uma circunferência mede  m. Calcule o ângulo que as tangentes formarão em tal circunferência que está traçada pelos extremos de uma corda com longitude de
m. Calcule o ângulo que as tangentes formarão em tal circunferência que está traçada pelos extremos de uma corda com longitude de  m.
m.
O raio de uma circunferência mede  m. Calcule o ângulo que as tangentes formarão em tal circunferência que está traçada pelos extremos de uma corda com longitude de
m. Calcule o ângulo que as tangentes formarão em tal circunferência que está traçada pelos extremos de uma corda com longitude de  m.
m.
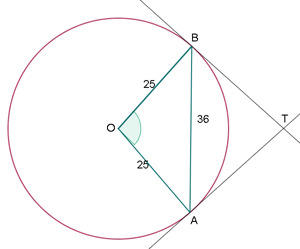
1) Aplicamos a lei de cossenos para calcular o ângulo 
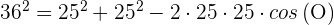

2) No quadrilátero 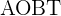 , os ângulos
, os ângulos  e
e  são retos.
são retos.
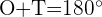

As diagonais de um paralelogramo medem  cm e
cm e  cm, e o ângulo que formam é de
cm, e o ângulo que formam é de  . Calcule os lados.
. Calcule os lados.
As diagonais de um paralelogramo medem 10 cm e 12 cm, e o ângulo que formam é de  . Calcule os lados.
. Calcule os lados.
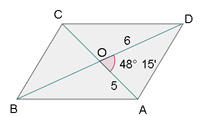
1) Calculamos 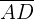 aplicando a lei de cossenos
aplicando a lei de cossenos
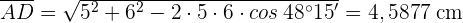
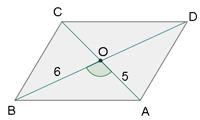
2) Calculamos o 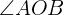 considerando que é suplementário ao
considerando que é suplementário ao 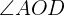 :
:

3) Aplicamos a lei de cossenos para calcular 
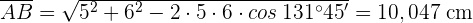
Resumir com IA:


