Teorema Fundamental do Cálculo
O Teorema Fundamental do Cálculo afirma que a derivada da integral 
de uma função contínua 
é próprio .
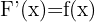
O Teorema Fundamental do Cálculo indica que a derivação e a integração são operações inversas.
Ao integrar uma função contínua e, em seguida, derivá-la, recupera-se a função original.
Exemplo:
Determine a derivada de:
1 Observamos que 
, portanto seu diferencial é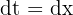 
2 Aplicando o Teorema Fundamental do Cálculo, temos:
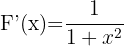
Exemplo:
Encontre a derivada de:
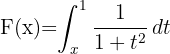
1 Primeiramente, trocamos os limites de integração; isso faz com que a integral mude de sinal:
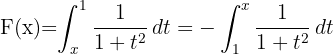
2 Observamos que , portanto seu diferencial é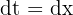
3 Aplicando o Teorema Fundamental do Cálculo, temos:
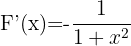
Exemplo:
Determine a derivada de:
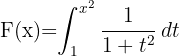
1 Observamos que 
, portanto seu diferencial é 
2 Aplicando o Teorema Fundamental do Cálculo, temos:
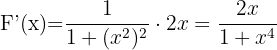
Teorema do Valor Médio para Integrais
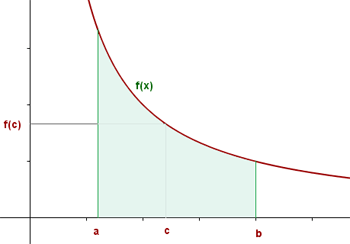
Se uma função é contínua em um intervalo fechado 
, então existe um ponto 
no interior do intervalo tal que:
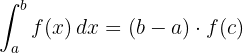
Exemplo:
Determine o valor de no Teorema do Valor Médio, para a função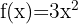 
no intervalo 
.
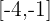1 Calculamos o valor da integral definida:
2 Como a função é contínua no intervalo 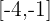, [−4,−1], pode-se aplicar o Teorema do Valor Médio para Integrais.
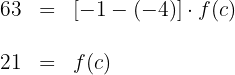
3 O valor de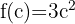 
, substituímos na igualdade anterior e resolvemos para
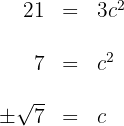
A solução positiva não é válida, pois não pertence ao intervalo.
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
