Teorema do seno
Cada lado de um triângulo é diretamente proporcional ao seno do ângulo oposto.
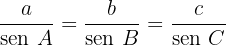
Usos
Este teorema é útil para resolver problemas se os dados fornecidos se enquadrarem em um dos seguintes casos:
1 Se conhecemos as medidas de dois lados de um triângulo e o ângulo oposto a um deles.
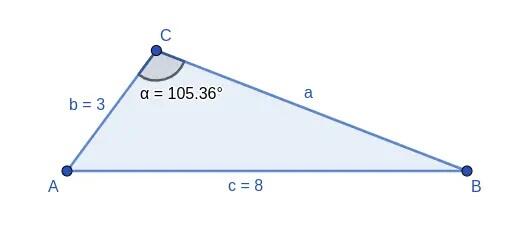
Aplicando o teorema, podemos obter imediatamente o ângulo oposto ao outro lado conhecido.
2 Se conhecemos as medidas de dois ângulos de um triângulo e de um dos lados:
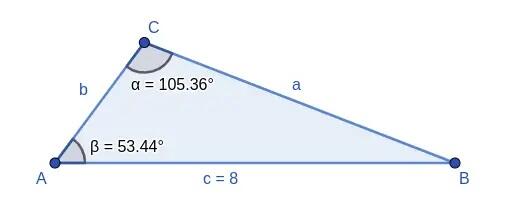
Aplicando o teorema, podemos obter imediatamente o lado oposto ao outro ângulo conhecido.
3 Também é possível aplicá-lo quando conhecemos dois ângulos do triângulo e um lado que não é oposto a nenhum deles, embora isso exija um passo adicional: determinar o terceiro ângulo do triângulo.
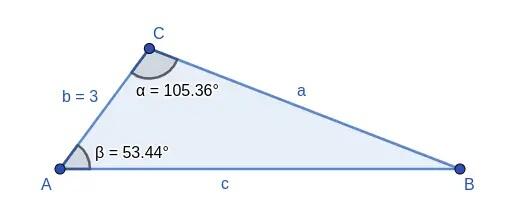
Isso é possível porque sabemos que a soma dos ângulos internos de um triângulo é 180°. Por exemplo, na imagem acima, o ângulo B é obtido subtraindo-se os outros dois ângulos de 180°:
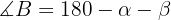
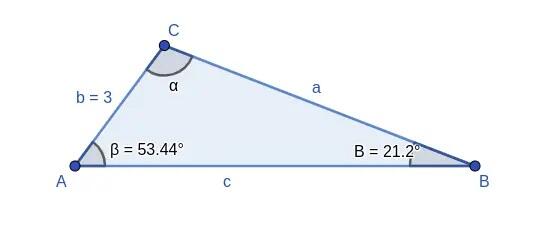
Ignorando um dos ângulos fornecidos originalmente, passamos a ter os dados de dois ângulos e o lado oposto a um deles, como no segundo caso mencionado nas aplicações.
Teorema do cosseno
Em um triângulo, o quadrado de cada lado é igual à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.
Usos
Este teorema é útil para resolver problemas:
1 Se conhecemos a medida de um ângulo e dos lados adjacentes a ele.
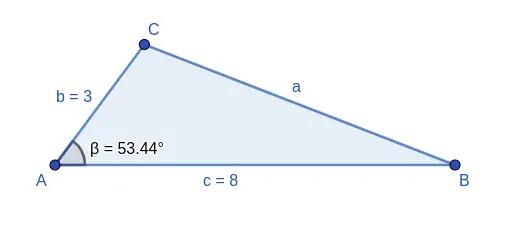
Aplicando o teorema, podemos obter o terceiro lado, ou seja, o lado oposto ao ângulo conhecido, pois:
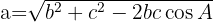
2 Se conhecemos as medidas dos três lados de um triângulo.
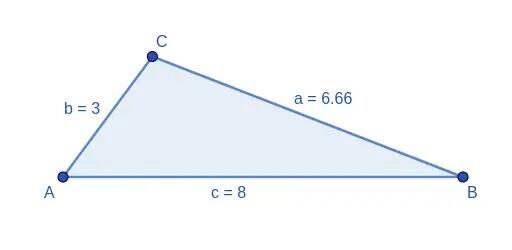
Aplicando o teorema, podemos obter qualquer um dos ângulos, pois:
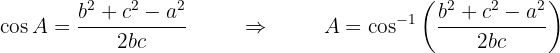
Teorema da tangente
O teorema da tangente relaciona um par de lados de um triângulo e seus respectivos ângulos opostos:
Usos:
Este teorema é tão útil quanto os teoremas do seno e do cosseno, mas é menos popular. Pode ser utilizado nos seguintes casos:
1 São conhecidos dois lados e um ângulo oposto.
2 São conhecidos dois ângulos e um lado oposto.
Área de um triângulo
1 A área 
de um triângulo é a metade do produto da base pela altura correspondente.
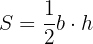
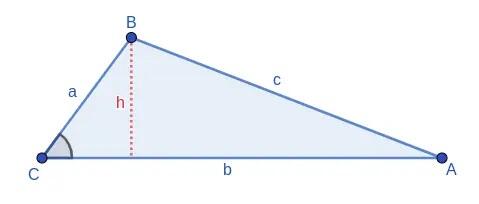
Por definição:
Substituindo 
na fórmula da área acima, obtemos o seguinte resultado.
2 A área de um triângulo é o semiproduto de dois de seus lados pelo seno do ângulo entre eles.
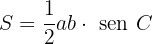
3 A área de um triângulo é o quociente entre o produto de seus lados e quatro vezes o raio da circunferência circunscrita.
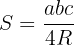
4 A área de um triângulo é igual ao produto do raio 
da circunferência inscrita pelo seu semiperímetro 
.
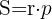
5 Fórmula de Herón: Seja o semiperímetro do triângulo, então,
Gostou desse artigo? Deixe uma nota!
Loading...
