
Obtenha os elementos da parábola
Dada a parábola 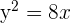 , calcule seu vértice, seu foco e a reta diretriz.
, calcule seu vértice, seu foco e a reta diretriz.
O parâmetro é

Trata-se de uma equação reduzida, dessa forma, o vértice está na origem
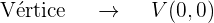
O termo quadrático na equação é o  , dessa forma, o eixo da parábola coincide com o eixo OX. Além disso, a parábola encontra-se no lado positivo do eixo OX, já que o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola coincide com o eixo OX. Além disso, a parábola encontra-se no lado positivo do eixo OX, já que o coeficiente que acompanha o termo no quadrático (neste caso  ) é 8, que é positivo. Assim
) é 8, que é positivo. Assim
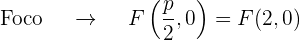
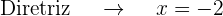
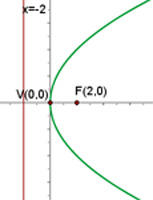
O gráfico da parábola 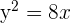 é:
é:
Dada a parábola 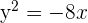 , calcule seu vértice, seu foco e a reta diretriz.
, calcule seu vértice, seu foco e a reta diretriz.
O parâmetro é

Trata-se de uma equação reduzida, dessa forma, o vértice está na origem
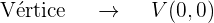
O termo quadrático na equação é o  , dessa forma, o eixo da parábola coincide com o eixo OX. Além disso, a parábola encontra-se no lado negativo do eixo OX, já que o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola coincide com o eixo OX. Além disso, a parábola encontra-se no lado negativo do eixo OX, já que o coeficiente que acompanha o termo no quadrático (neste caso  ) é -8, que é negativo. Assim
) é -8, que é negativo. Assim
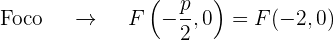
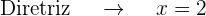
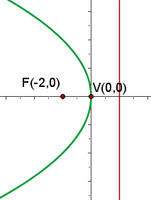
O gráfico da parábola 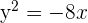 é:
é:
Dada a parábola 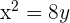 , calcule seu vértice, seu foco e a reta diretriz.
, calcule seu vértice, seu foco e a reta diretriz.
O parâmetro é

Trata-se de uma equação reduzida, dessa forma, o vértice está na origem
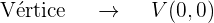
O termo quadrático na equação é o  , dessa forma, o eixo da parábola coincide com o eixo OY. Além disso, a parábola encontra-se no lado positivo do eixo OY, já que o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola coincide com o eixo OY. Além disso, a parábola encontra-se no lado positivo do eixo OY, já que o coeficiente que acompanha o termo no quadrático (neste caso  ) é 8, que é positivo. Assim
) é 8, que é positivo. Assim
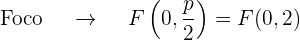
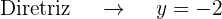
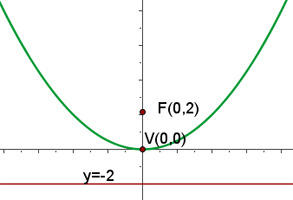
O gráfico da parábola 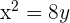 é:
é:
Dada a parábola 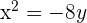 , calcule seu vértice, seu foco e a reta diretriz.
, calcule seu vértice, seu foco e a reta diretriz.
O parâmetro é

Trata-se de uma equação reduzida, dessa forma, o vértice está na origem
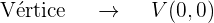
O termo quadrático na equação é o  , dessa forma, o eixo da parábola coincide com o eixo OY. Além disso, a parábola encontra-se no lado negativo do eixo OY, já que o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola coincide com o eixo OY. Além disso, a parábola encontra-se no lado negativo do eixo OY, já que o coeficiente que acompanha o termo no quadrático (neste caso  ) é 8, que é negativo. Assim
) é 8, que é negativo. Assim
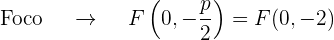
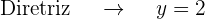
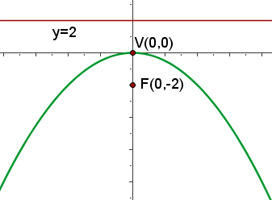
O gráfico da parábola 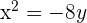 é:
é:
Dada a parábola 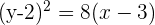 , calcule seu vértice, seu foco e a reta diretriz.
, calcule seu vértice, seu foco e a reta diretriz.
O parâmetro é

Não se trata de uma equação reduzida, dessa forma, o vértice está em

O termo quadrático na equação é  dessa forma, o eixo da parábola é paralelo ao eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso
dessa forma, o eixo da parábola é paralelo ao eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso  ) é 8, que é positivo, portanto, o foco está ao lado direito do vértice
) é 8, que é positivo, portanto, o foco está ao lado direito do vértice
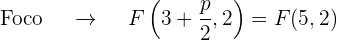
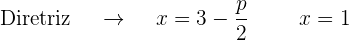
O gráfico da parábola 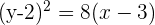 é:
é:
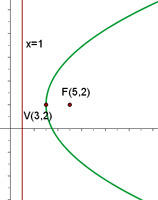
Dada a parábola 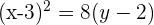 , calcule seu vértice, seu foco e a reta diretriz.
, calcule seu vértice, seu foco e a reta diretriz.
O parâmetro é

Não se trata de uma equação reduzida, dessa forma, o vértice está em

O termo quadrático na equação é  , dessa forma, o eixo da parábola é paralelo ao eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola é paralelo ao eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso  ) é 8, que é positivo, portanto, o foco está ao lado direito do vértice
) é 8, que é positivo, portanto, o foco está ao lado direito do vértice

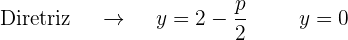
O gráfico da parábola 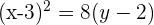 é:
é:
Determine, em forma reduzida, as equações das seguintes parábolas, indicando o valor do parâmetro, as coordenadas do foco e a equação da diretriz.
a)  Isolamos o termo
Isolamos o termo 


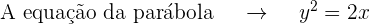
O parâmetro é

Trata-se de uma equação reduzida, dessa forma, o vértice está na origem
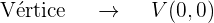
O termo quadrático na equação é  , dessa forma, o eixo da parábola coincide com o eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola coincide com o eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso  ) é 2, que é positivo, portanto, o foco está ao lado direito do vértice
) é 2, que é positivo, portanto, o foco está ao lado direito do vértice
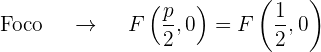
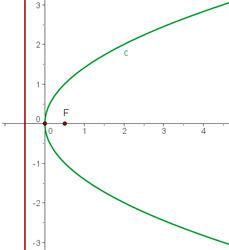
O gráfico da parábola  é:
é:
b) 
Isolamos o término 


O parâmetro é

Trata-se de uma equação reduzida, dessa forma, o vértice está na origem
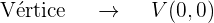
O termo quadrático na equação é  , dessa forma, o eixo da parábola coincide com o eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola coincide com o eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso  ) é
) é 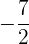 que é negativo, portanto, o foco está ao lado esquerdo do vértice
que é negativo, portanto, o foco está ao lado esquerdo do vértice
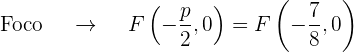
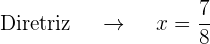
O gráfico da parábola  é:
é:
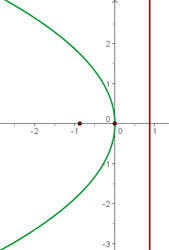
c) 
Isolamos o termo 


O parâmetro é

Trata-se de uma equação reduzida, dessa forma, o vértice está na origem
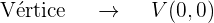
O termo quadrático na equação é  , dessa forma, o eixo da parábola coincide com o eixo OY. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola coincide com o eixo OY. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso  ) é
) é 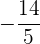 que é negativo, portanto, o foco está abaixo do vértice
que é negativo, portanto, o foco está abaixo do vértice
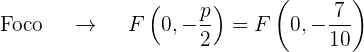
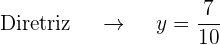
O gráfico da parábola 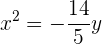 é:
é:
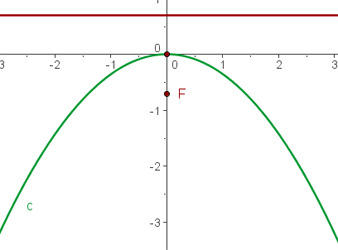
Calcule as coordenadas do vértice e dos focos e as equações das diretrizes das parábolas:
Calcule as coordenadas do vértice e dos focos e as equações das diretrizes das parábolas:
a) 
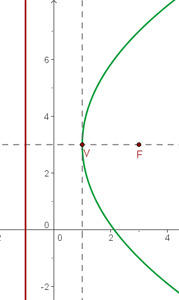
Completamos o quadrado

Simplificamos
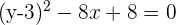
Isolamos
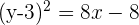

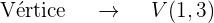
O parâmetro é

O termo quadrático na equação é  , dessa forma, o eixo da parábola é paralelo ao eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola é paralelo ao eixo OX. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso  ) é 8, que é positivo, portanto, o foco está ao lado direito do vértice
) é 8, que é positivo, portanto, o foco está ao lado direito do vértice
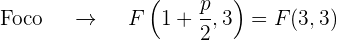
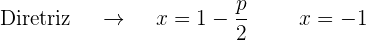
b) 
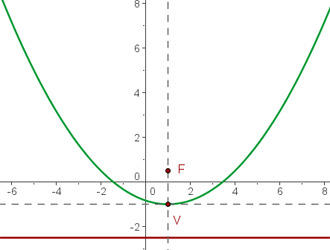
Completamos o quadrado

Simplificamos

Isolamos
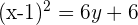

Então,

O parâmetro é

O termo quadrático na equação é  , dessa forma, o eixo da parábola é paralelo ao eixo OY. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso
, dessa forma, o eixo da parábola é paralelo ao eixo OY. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso  ) é 6, que é positivo, portanto, o foco está mais acima do vértice
) é 6, que é positivo, portanto, o foco está mais acima do vértice
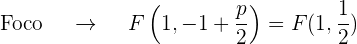
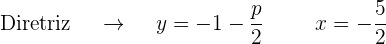
c) 
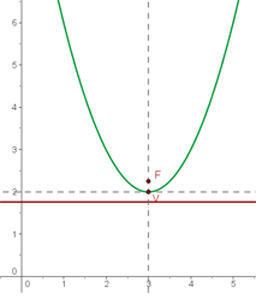
Completamos o quadrado

Simplificamos
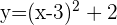
Isolamos
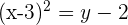

O parâmetro é

O termo quadrático na equação é  dessa forma, o eixo da parábola é paralelo ao eixo OY. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso
dessa forma, o eixo da parábola é paralelo ao eixo OY. Além disso, o coeficiente que acompanha o termo no quadrático (neste caso  ) é 1, que é positivo, portanto, o foco está mais acima do vértice
) é 1, que é positivo, portanto, o foco está mais acima do vértice
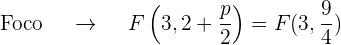
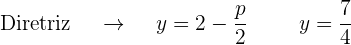
Obtenha a equação da parábola
Determine as equações das parábolas que têm:
- Diretriz
 , foco
, foco 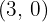 .
. - Diretriz
 , vértice
, vértice  .
. - Diretriz
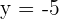 , foco
, foco  .
. - Diretriz
 , foco
, foco 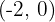 .
. - Foco
 , vértice
, vértice  .
. - Foco
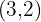 , vértice
, vértice 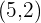 .
. - Foco
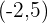 , vértice
, vértice 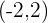 .
. - Foco
 , vértice
, vértice 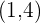 .
.
Determine as equações das parábolas que têm:
a) Diretriz  , foco
, foco 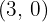 .
.
Primeiro calculamos a distância entre o foco e a diretriz, para assim obter o parâmetro  .
.

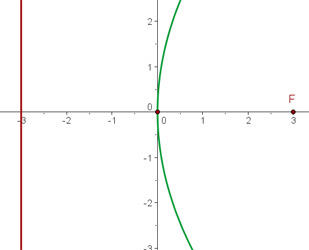
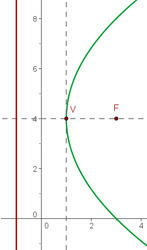
Como o foco encontra-se sobre o eixo OX, a diretriz é paralela ao eixo OY e são equidistantes da origem, trata-se de uma equação reduzida
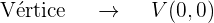
Então, como o eixo coincide com o eixo OX e o foco está mais à direita que o vértice, a equação está dada por

b) Diretriz  , vértice
, vértice  .
.
Primeiro calculamos a distância entre o vértice e a diretriz, para assim obter 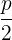 .
.

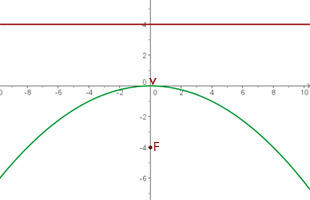
Devemos notar que o vértice está na origem e a diretriz é paralela ao eixo OX, dessa forma, trata-se de uma equação reduzida.
Como o eixo coincide com o eixo OY e o foco está mais abaixo que o vértice, a equação será
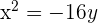
c) Diretriz 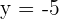 , foco
, foco  .
.
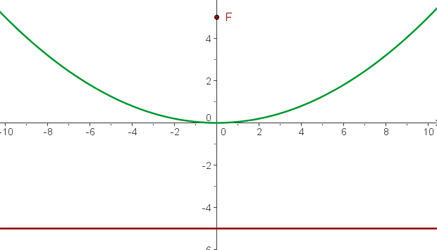
Primeiro calculamos a distância entre o foco e a diretriz, para assim obter o parâmetro  .
.
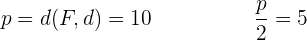
Devemos notar que a diretriz é paralela ao eixo OX, que o foco está sobre o eixo OY e são equidistantes da origem. Dessa forma, trata-se de uma equação reduzida.
Como o foco está mais acima do que a diretriz, a equação será
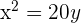
d) Diretriz  , foco
, foco 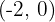 .
.
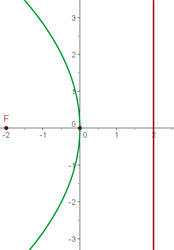
Primeiro calculamos a distância entre o foco e a diretriz, para assim obter o parâmetro  .
.
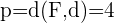
Devemos notar que a diretriz é paralela ao eixo OY, que o foco está sobre o eixo OX e são equidistantes da origem. Dessa forma, trata-se de uma equação reduzida.
Como o foco está mais à esquerda do que a diretriz, a equação será
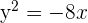
e) Foco  , vértice
, vértice  .
.
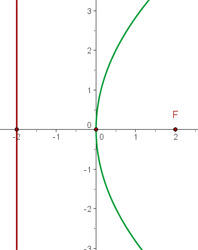
Primeiro calculamos a distância entre o foco e o vértice, para assim obter o parâmetro 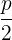 .
.
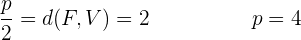
Devemos notar que a diretriz é paralela ao eixo OY, que o foco está sobre o eixo OX e são equidistantes da origem. Dessa forma, trata-se de uma equação reduzida.
Como o foco está mais à direita do que a diretriz, a equação será
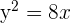
f) Foco 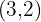 , vértice
, vértice 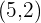 .
.
Primeiro calculamos a distância entre o foco e a diretriz, para assim obter 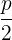 .
.
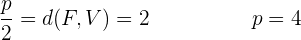
Devemos notar que a diretriz é paralela ao eixo OY.
Como o foco está mais à esquerda do que o vértice, a equação será
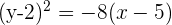
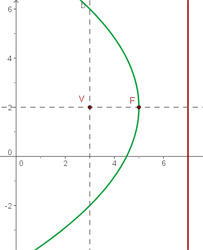
g) Foco 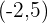 , vértice
, vértice 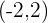 .
.
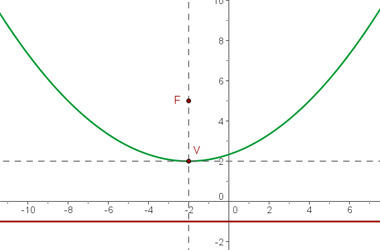
Primeiro calculamos a distância entre o foco e a vértice, para assim obter 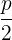 .
.
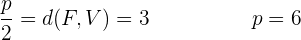
Devemos notar que a diretriz é paralela ao eixo OX.
Como o foco está mais acima do que o vértice, a equação será

h) Foco  , vértice
, vértice 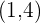 .
.
Primeiro calculamos a distância entre o foco e o vértice, para assim obter o parâmetro  .
.
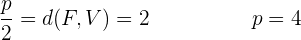
Devemos notar que a diretriz é paralela ao eixo OY.
Como o foco está mais à esquerda do que o vértice, a equação será

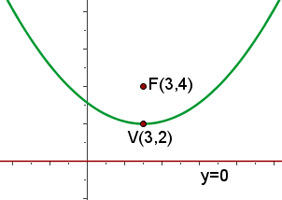
Encontre a equação da parábola cujo vértice coincide com a origem de coordenadas e que passa pelo ponto  , sendo seu eixo OX.
, sendo seu eixo OX.
Como seu vértice é a origem e seu eixo coincide com o eixo OX do plano, sua equação é na forma reduzida. Em particular, é

Passa pelo ponto (3,4), dessa forma, suas coordenadas cumprem a equação anterior, isso é:
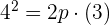
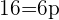
Dividimos entre 3

Então, a equação fica assim
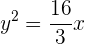
Escreva a equação da parábola com eixo paralelo a OY, vértice em OX e que passa pelos pontos  e
e 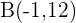 .
.
Do problema, sabemos que
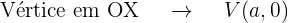
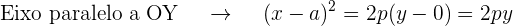
Como a curva passa pelos pontos A e B, suas coordenadas devem satisfazer a equação da parábola,
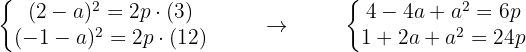
Pegamos a primeira equação e multiplicamos por 4 para obter:

Subtraímos a segunda equação, isso é, somamos com o negativo

Para assim obter


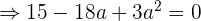
Simplificamos dividindo tudo entre 3
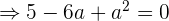
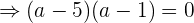
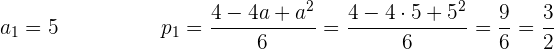
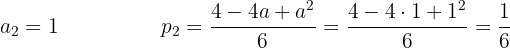
As duas soluções de  nos dão duas soluções de equações de parábolas diferentes.
nos dão duas soluções de equações de parábolas diferentes.

Determine a equação da parábola que tem como diretriz a reta: 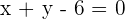 e como foco a origem de coordenadas.
e como foco a origem de coordenadas.
Sabemos que a distância de um ponto 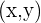 em relação a diretriz deve ser igual à distância desse ponto em relação ao foco, isso é
em relação a diretriz deve ser igual à distância desse ponto em relação ao foco, isso é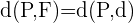

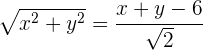
Elevamos o quadrado para desfazermos da raiz
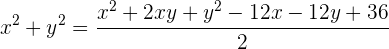
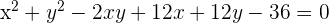
Encontre a equação da parábola do eixo vertical e que passa pelos pontos: 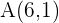 ,
, 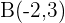 ,
,  .
.
A equação tem que ser com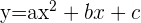
Se passa pelos pontos A, B e C, suas coordenadas cumprem a equação anterior
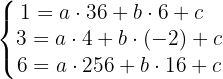
Resolvendo o sistema de 3 incógnitas, obtemos
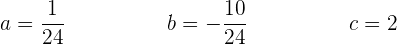
Por fim

Determine a equação da parábola que tem como diretriz a reta:  e como foco o ponto
e como foco o ponto  .
.
Determine a equação da parábola que tem como diretriz a reta: y = 0 e como foco o ponto (2, 4).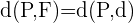
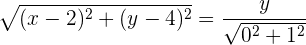
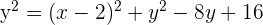
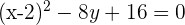
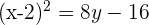
Por fim, a equação parabólica que obtemos é:

Calcule a posição relativa da reta  em relação à parábola
em relação à parábola 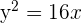 .
.
Calcule a posição relativa da reta r ≡ x + y − 5 = 0 em relação à parábola y² = 16 x.
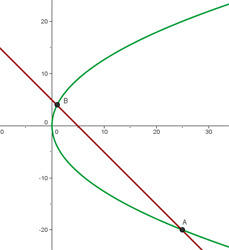

Calculamos


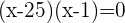
Resolvemos

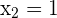
Resumir com IA:












