Temas
Definição de Distribuição de Frequências
A distribuição de frequências ou tabela de frequências é uma organização em forma de tabela dos dados estatísticos, atribuindo a cada dado a sua frequência correspondente.
Tipos de Frequências
Frequência absoluta
A frequência absoluta é o número de vezes que um determinado valor aparece em um estudo estatístico.
Ao jogar uma moeda 
vezes, saem 
caras
É representada por 
, embora outros autores a representem como 
.
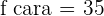
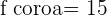
A soma das frequências absolutas é igual ao número total de dados, representado por 
.
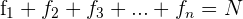
Para indicar resumidamente essas somas, utiliza-se a letra grega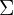 
(sigma maiúscula) que significa soma ou somatório.
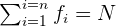
Frequência relativa
A frequência relativa é o quociente entre a frequência absoluta de um determinado valor e o número total de dados.
Pode ser expressa em percentagem e é representada por .
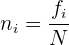
A frequência relativa é um número compreendido entre 
e 
.
A soma das frequências relativas é igual a .
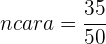
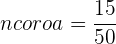
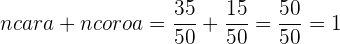
Frequência acumulada
A frequência acumulada é a soma das frequências absolutas de todos os valores inferiores ou iguais ao valor considerado.
É representada por 
.
Frequência relativa acumulada
A frequência relativa acumulada é o quociente entre a frequência acumulada de um determinado valor e o número total de dados.
Pode ser expressada em porcentagem.
Exemplo:
Durante o mês de julho, em uma cidade, foram registradas as seguintes temperaturas máximas:
.
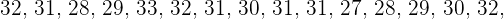
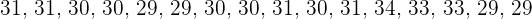Na primeira coluna da tabela, colocamos a variável ordenada de menor para maior
Na segunda, fazemos a contagem
Na terceira, anotamos a frequência absoluta
Na quarta, anotamos a frequência acumulada:
Na primeira célula, colocamos a primeira frequência absoluta:
Na segunda célula, somamos o valor da frequência acumulada anterior mais a frequência absoluta correspondente:
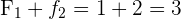
Na terceira célula, somamos o valor da frequência acumulada anterior mais a frequência absoluta correspondente:
A última célula tem que ser igual a (soma de ).
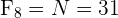
Na quinta coluna, disponibilizamos as frequências relativas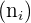 
que são o resultado da divisão de cada frequência absoluta por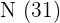 
Na sexta, anotamos a frequência relativa acumulada 
.
Na primeira célula, colocamos a primeira frequência relativa acumulada.
Na segunda célula, somamos o valor da frequência relativa acumulada anterior mais a frequência relativa correspondente, e assim por diante até a última, que tem que ser igual a .
| Altura | Nº de jogadores |
|---|---|
| [1.70, 1.75) | 1 |
| [1.75, 1.80) | 3 |
| [1.80, 1.85) | 4 |
| [1.85, 1.90) | 8 |
| [1.90, 1.95) | 5 |
| [1.95, 2.00) | 2 |
Esse tipo de tabelas de frequência é usado com variáveis discretas.
Distribuição de Frequências Agrupadas
A distribuição de frequências agrupadas ou tabela com dados agrupados é utilizada se as variáveis assumem um grande número de valores ou se a variável é contínua.
Os valores são agrupados em intervalos que tenham a mesma amplitude, chamados de classes. A cada classe é atribuída a sua frequência correspondente.
Limites da Classe
Cada classe é delimitada pelo limite inferior da classe e pelo limite superior da classe.
Amplitude da classe
A amplitude da classe é a diferença entre o limite superior e o limite inferior da classe.
Marca da classe
A marca da classe é o ponto médio de cada intervalo e é o valor que representa todo o intervalo para o cálculo de alguns parâmetros.
A marca da classe é representada por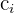 
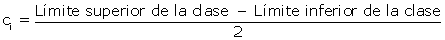
Construção de uma Tabela de Dados Agrupados
.
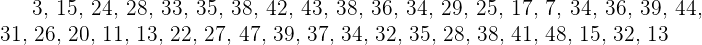1º Localizam-se os valores mínimo e máximo da distribuição. Neste caso, são 
e 
.
2º Subtraem-se e procura-se um número inteiro um pouco maior que a diferença e que seja divisível pelo número de intervalos que se quer estabelecer
É conveniente que o número de intervalos oscile entre 
e 
.
Neste caso,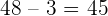 
, aumentamos o número para , 
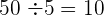intervalos.
Formam-se os intervalos tendo em mente que o limite inferior de uma classe pertence ao intervalo, mas o limite superior não pertence ao intervalo, ele é contado no próximo intervalo.
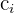é a marca de classe, que é o ponto médio de cada intervalo:
| xi | fi | Fi | xi · fi | xi² · fi | |
|---|---|---|---|---|---|
| [1.70, 1.75) | 1.725 | 1 | 1 | 1.725 | 2.976 |
| [1.75, 1.80) | 1.775 | 3 | 4 | 5.325 | 9.452 |
| [1.80, 1.85) | 1.825 | 4 | 8 | 7.3 | 13.323 |
| [1.85, 1.90) | 1.875 | 8 | 16 | 15 | 28.125 |
| [1.90, 1.95) | 1.925 | 5 | 21 | 9.625 | 18.53 |
| [1.95, 2.00) | 1.975 | 2 | 23 | 3.95 | 7.802 |
| 23 | 42.925 | 80.213 |
Se você ainda tem dúvidas com a construção de tabelas de frequência, procure um professor particular de matemática no Superprof. Ficamos felizes em ajudar!
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
