Temas

O que é a solução de uma inequação?
A solução de uma inequação é o conjunto de valores da variável que torna verdadeira a inequação. Esse conjunto de soluções representa uma região geométrica: na reta real, quando a inequação tem uma variável; ou no plano, quando possui duas variáveis.
Exemplo:
- A inequação
 gera a seguinte região no plano:
gera a seguinte região no plano:
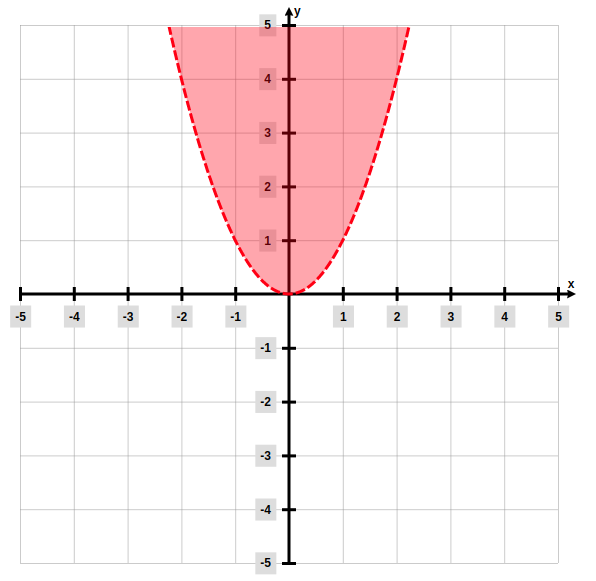
Sistema de inequações
A solução de um sistema de inequações é a interseção das regiões que correspondem à solução de cada inequação tomada separadamente.
Dizemos que um sistema é linear quando, em ambos os lados de cada inequação, aparecem apenas expressões de primeiro grau.
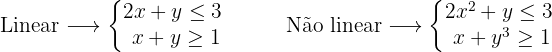
Exemplos de sistemas de inequações lineares com duas incógnitas
Vamos resolver o sistema:
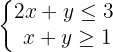
Representamos a região solução da primeira inequação
1. Transformamos a desigualdade em igualdade:

2 . Atribuímos dois valores a uma das variáveis para obter dois pontos:


3 Ligando os dois pontos, obtemos uma reta.
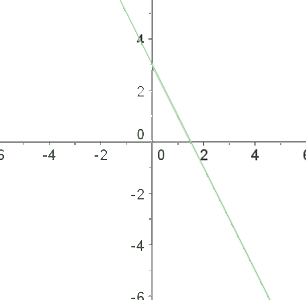
Finalmente, escolhemos um ponto, por exemplo, (0, 0) e o substituímos na desigualdade. Se a desigualdade for satisfeita, a solução corresponde ao semiplano onde o ponto se encontra; caso contrário, a solução será o semiplano oposto.


A desigualdade é satisfeita.
Como ela é satisfeita, a solução é o semiplano onde está o ponto (0, 0), incluindo a reta.

Representamos a região solução da segunda inequação
1 Transformamos a desigualdade em igualdade.
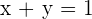
2 Atribuímos dois valores a uma das variáveis, obtendo dois pontos.
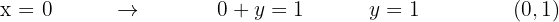
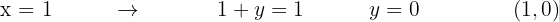
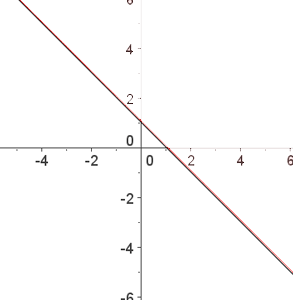
3 Escolhemos novamente o ponto (0, 0) e o substituímos na desigualdade.
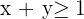
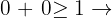
A desigualdade não se satisfaz. Portanto, a solução é o semiplano onde o ponto (0, 0) não se encontra, incluindo a reta.

A solução do sistema é a interseção das regiões
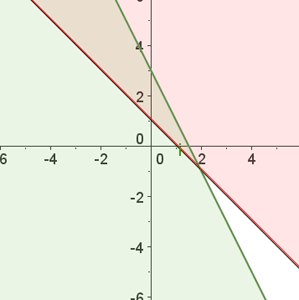
Exemplos de sistemas de inequações lineares com uma incógnita
Cada inequação é resolvida separadamente. O conjunto solução do sistema é a interseção dos conjuntos solução de cada inequação.
1

Resolvemos a primeira inequação

Resolvemos a segunda inequação
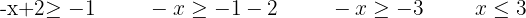
Consideramos a interseção das soluções:

Intervalo de solução é: [−1, 3]
2
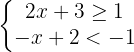
Resolvemos a primeira inequação

Resolvemos a segunda inequação
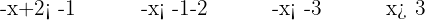
Consideramos a interseção das soluções:
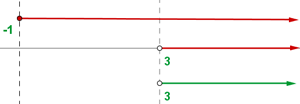
Intervalo de solução é: (3, ∞)
3

Resolvemos a primeira inequação

Resolvemos a segunda inequação

Consideramos a interseção das soluções:

Não existe solução.
Resumir com IA:












