Escreva a equação da circunferência de centro  e raio
e raio  .
.
Escreva a equação da circunferência de centro  e raio
e raio  .
.
a) Substituímos os dados na equação ordinária da circunferência: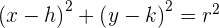
onde:
 são as coordenadas do centro e
são as coordenadas do centro e  é o raio.
é o raio.
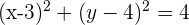
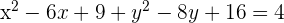
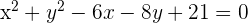
Dada a circunferência da equação  , encontre o centro e o raio.
, encontre o centro e o raio.
Dada a circunferência da equação  , encontre o centro e o raio. Convertemos a equação geral para a forma ordinária
, encontre o centro e o raio. Convertemos a equação geral para a forma ordinária 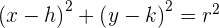 ; para isso seguimos o passo a passo:
; para isso seguimos o passo a passo:
a) Reescrevemos a equação ordenando os  e
e  e completamos os trinômios quadrados perfeitos
e completamos os trinômios quadrados perfeitos 
b) Fatoramos os trinômios quadrados perfeitos

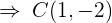 y
y 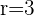
Determine as coordenadas do centro e o raio das circunferências:
Determine as coordenadas do centro e o raio das circunferências:
a) 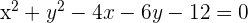
Reescrevemos a equação na sua forma ordinária:
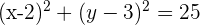
 e
e 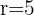
b) 
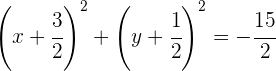 e
e 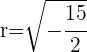
Já que  é imaginário, ele não é uma circunferência real
é imaginário, ele não é uma circunferência real
c) 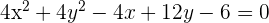
Dividimos por 4 e reescrevemos a equação na forma ordinária:
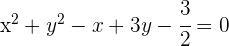
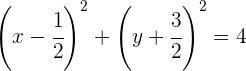
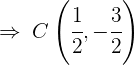 e
e 
d) 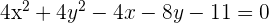
Dividimos por 4 e reescrevemos a equação na forma ordinária: 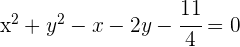
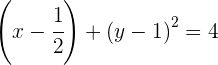
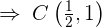 e
e 
Calcule a equação da circunferência que tem por centro 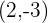 e é tangente ao eixo das abscissas.
e é tangente ao eixo das abscissas.
Calcule a equação da circunferência que tem por centro 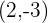 e é tangente ao eixo das abscissas.
e é tangente ao eixo das abscissas.
1) Fazemos o gráfico da circunferência a partir dos dados:
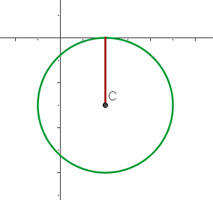
2) A partir dos dados podemos deduzir que
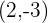

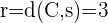
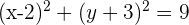
Calcule a equação da circunferência que tem por centro 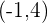 e é tangente ao eixo das ordenadas.
e é tangente ao eixo das ordenadas.
Calcule a equação da circunferência que tem por centro 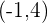 e é tangente ao eixo das ordenadas.
e é tangente ao eixo das ordenadas.
1) Fazemos o gráfico da circunferência a partir dos dados:
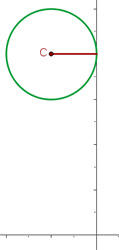
2) A partir do gráfico podemos deduzir que
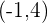
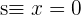
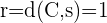

Calcule a equação da circunferência que tem por centro o ponto de interseção das retas  ,
,  , e um raio igual a
, e um raio igual a  .
.
Calcule a equação da circunferência que tem por centro o ponto de interseção das retas  ,
,  , e um raio igual a
, e um raio igual a  .
.
1) Propomos um sistema de equação com as retas. A solução do sistema de equações corresponde ao centro da circunferência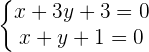

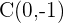
2) Substituímos 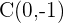 e
e 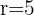 na forma ordinária
na forma ordinária
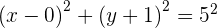
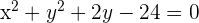
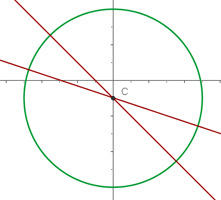
Encontre a equação da circunferência concêntrica com a equação  , e que passa pelo ponto
, e que passa pelo ponto 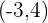
Encontre a equação da circunferência concêntrica com a equação  , e que passa pelo ponto
, e que passa pelo ponto 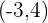 .
.
1) Por serem concêntricas têm o mesmo centro:
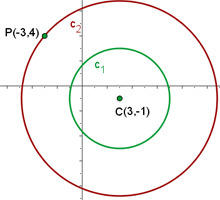
2) Calculamos o centro da circunferência 
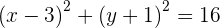
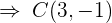
3) Para calcular o raio calculamos a distância de 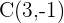 a
a 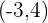

4) Substituímos o centro e o raio na forma ordinária
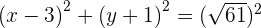

Encontre a equação da circunferência que tem por centro o ponto 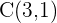 e é tangente à reta:
e é tangente à reta:  .
.
Encontre a equação da circunferência que tem por centro o ponto 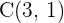 e é tangente à reta:
e é tangente à reta:  .
.
1) O raio é calculado com a distância do ponto 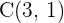 em relação a reta
em relação a reta 
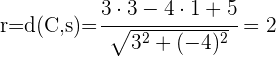
2) Substituímos 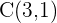 e
e  na forma ordinária
na forma ordinária
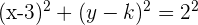
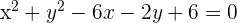
Encontre a equação da circunferência que passa pelos pontos 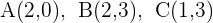 .
.
Encontre a equação da circunferência que passa pelos pontos 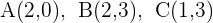 .
.
1) Considerando a equação geral de uma circunferência como  , substituímos os pontos e construímos um sistema de equações:
, substituímos os pontos e construímos um sistema de equações:
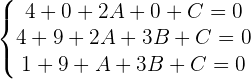
2) Resolvemos o sistema de equações e substituímos na forma geral:

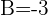
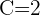

Encontre a equação da circunferência circunscrita ao triângulo de vértices: 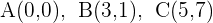 .
.
Encontre a equação da circunferência circunscrita ao triângulo de vértices: 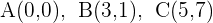 .
.
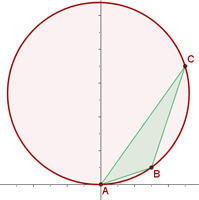
1) Considerando que os vértices do triângulo são pontos em que passa a circunferência, podemos considerar a equação da circunferência como
 e substituir os pontos:
e substituir os pontos:
2) Resolvemos o sistema de equações e substituímos na forma geral:
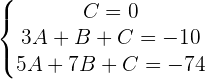
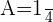

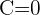
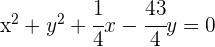
Encontre a equação da circunferência que passa pelos pontos  e
e 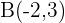 e tem seu centro sobre a reta:
e tem seu centro sobre a reta: 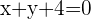 .
.
Encontre a equação da circunferência que passa pelos pontos  e
e 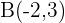 e tem seu centro sobre a reta
e tem seu centro sobre a reta 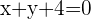 .
.
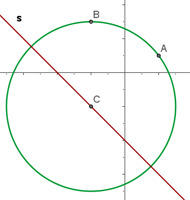
1) Consideramos que o ponto  é o centro da circunferência e encontra-se sobre a reta
é o centro da circunferência e encontra-se sobre a reta 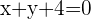 . Podemos assim propor o sistema:
. Podemos assim propor o sistema:

2) Das duas primeiras equações obtemos:
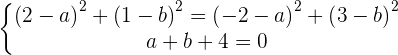
3) Resolvendo o sistema:
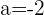

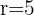
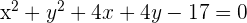
Calcule a equação da circunferência que passa pelo ponto 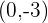 , cujo raio é
, cujo raio é  e cujo centro encontra-se na bissetriz do primeiro e terceiro quadrantes.
e cujo centro encontra-se na bissetriz do primeiro e terceiro quadrantes.
Calcule a equação da circunferência que passa pelo ponto 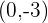 , cujo raio é
, cujo raio é  e cujo centro encontra-se na bissetriz do primeiro e terceiro quadrantes.
e cujo centro encontra-se na bissetriz do primeiro e terceiro quadrantes.
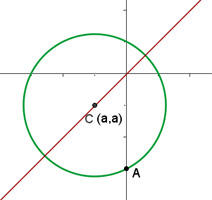
1) Consideramos que o ponto  é o centro da circunferência, além disso, a bissetriz do primeiro e terceiro quadrante é a reta
é o centro da circunferência, além disso, a bissetriz do primeiro e terceiro quadrante é a reta 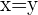 :
:



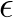

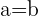

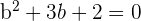
2) Obtemos duas soluções para  :
:


3) Para 

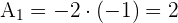
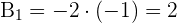
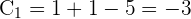
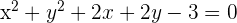
4) Para 
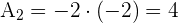
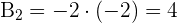
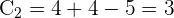
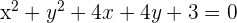
Os extremos do diâmetro de uma circunferência são os pontos 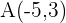 e
e  . Qual é a equação desta circunferência?
. Qual é a equação desta circunferência?
Os extremos do diâmetro de uma circunferência são os pontos 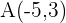 e
e  . Qual é a equação desta circunferência?
. Qual é a equação desta circunferência?
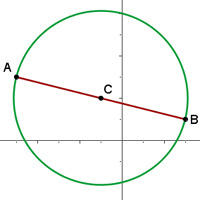
1) O raio da circunferência será a metade da distância entre os pontos  e
e  :
:

2) O centro da circunferência será encontrado no ponto médio entre os pontos  e
e  :
:

3) Obtemos os coeficientes  e
e  para a fórmula
para a fórmula 

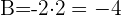
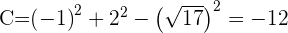

Encontre a equação da circunferência concêntrica na circunferência  que seja tangente à reta
que seja tangente à reta 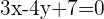 .
.
Encontre a equação da circunferência concêntrica na circunferência  que seja tangente à reta
que seja tangente à reta 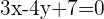 .
.
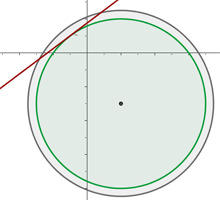
1) Obtemos o centro da circunferência com coordenadas  :
:

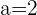
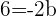
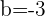
2) O raio será a distância entre  e a reta
e a reta 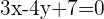 :
:
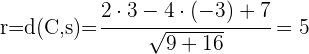
3) Obtemos os coeficientes  e
e  para a fórmula
para a fórmula 


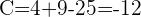
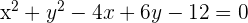
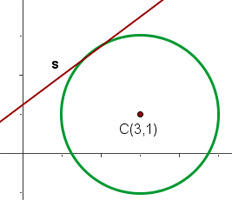
Calcule a posição relativa da circunferência 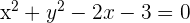 e a reta
e a reta 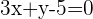 .
.
Calcule a posição relativa da circunferência 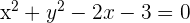 e a reta
e a reta 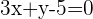 .
.
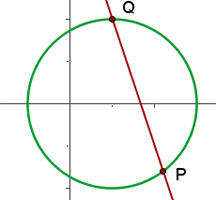
1) Propomos um sistema de equação entre a equação da circunferência e a equação da reta para encontrar suas interseções
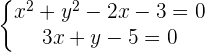
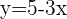
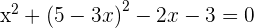
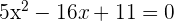

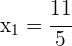
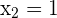
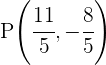

Já que existem dois pontos de interseção, podemos dizer que a reta e a circunferência são secantes.
Encontre a posição relativa da circunferência 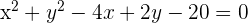 com as retas:
com as retas:
a) Encontre a posição relativa da circunferência 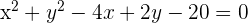 com as retas:A
com as retas:A 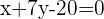
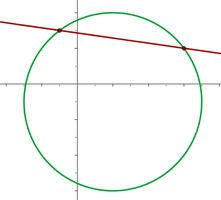
Propomos um sistema de equação entre a equação da circunferência e a equação da reta para encontrar suas interseções:
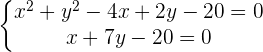

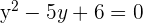
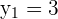

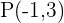

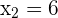
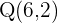
Já que existem dois pontos de interseção, podemos dizer que a reta e a circunferência são secantes.
b) 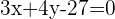
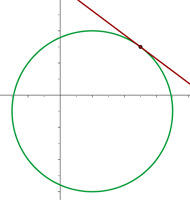
Propomos um sistema de equação entre a equação da circunferência e a equação da reta para encontrar suas interseções:


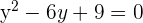



Já que existe apenas um ponto de interseção entre a circunferência e a reta, podemos dizer que são tangentes.
c) 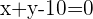
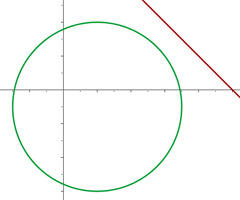
Propomos um sistema de equação entre a equação da circunferência e a equação da reta para encontrar suas interseções:
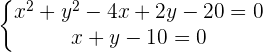
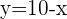

 \Delta =(-13)^{2}-4.50< 0[/latex]
\Delta =(-13)^{2}-4.50< 0[/latex]
Já que não existem pontos de interseção entre a reta e a circunferência podemos dizer que são exteriores.
Resumir com IA:


