Temas

Estude a monotonicidade, a convergência ou divergência e os limites das sequências
Estude a monotonicidade, a convergência ou divergência e os limites das sequências.
1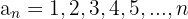
2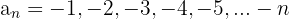
3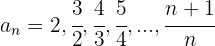
4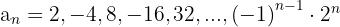
5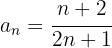
6
7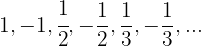
8
1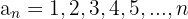
É crescente.
Está limitada inferiormente.
Cotas inferiores: 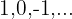
O mínimo é: 
Não está limitada superiormente.
Divergente
2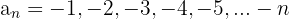
É decrescente.
Está limitada superiormente.
Cotas superiores: 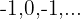
O máximo é: 
Não está limitada inferiormente.
Divergente
3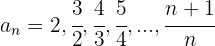
É decrescente.
Está limitada superiormente.
Cotas superiores: 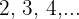
O máximo é: 
Está limitada inferiormente.
Cotas inferiores: 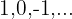
O ínfimo é: 
Convergente, 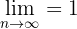
4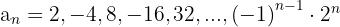
Não é monótona.
Não está limitada.
Não é convergente nem divergente.
5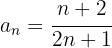
Os primeiros termos desta sequência são:
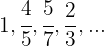
É monotônica estritamente decrescente.
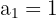


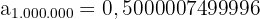
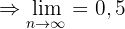
Sequência convergente
Por ser decrescente,  é uma cota superior, o máximo.
é uma cota superior, o máximo.
 é uma cota inferior, o ínfimo ou extremo inferior.
é uma cota inferior, o ínfimo ou extremo inferior.
Portanto, a sequência está limitada.
$0,5 < a_{n} \leq 1$
6
Os primeiros termos da sequência são:

Não é monótona.
Não é convergente nem divergente.
Não está limitada.
7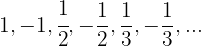
Não é monótona.
É convergente porque 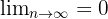
Está limitada superiormente,  é o máximo.
é o máximo.
Está limitada inferiormente,  é o mínimo.
é o mínimo.
Está limitada.
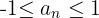
8
Os primeiros termos da sequência são:
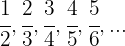
É monotônica estritamente crescente.
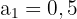

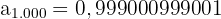

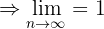
Sequência convergente
Está limitada inferiormente, é o mínimo
Está limitada superiormente.  é supremo.
é supremo.
Portanto, a sequência está limitada.
 \( 0,5 < a_{n} \leq 1 \) [/latex]
\( 0,5 < a_{n} \leq 1 \) [/latex]
Encontre o termo geral das seguintes sequências
Encontre o termo geral das seguintes sequências
1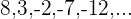
2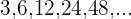
3
4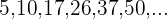
5
6
7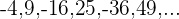
8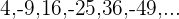
9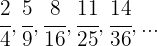
10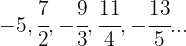
1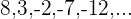
Podemos obter a diferença entre os termos consecutivos:

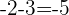
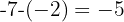
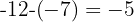
Como a diferença é constante, 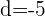
É uma progressão aritmética
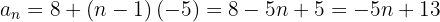
2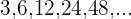
Podemos dividir cada termo pelo seu antecessor:

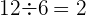
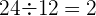
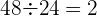
Como o quociente é constante, 
trata-se uma progressão geométrica
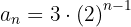
3
A sequência pode ser reescrita como:
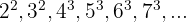
Observamos que as bases estão em progressão aritmética, com  ,e o expoente é constante. Logo, podemos escrever a base da sequência:
,e o expoente é constante. Logo, podemos escrever a base da sequência:
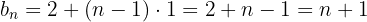
Portanto, o termo geral é:
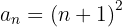
4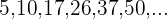
Cada termo desta sequência é o próximo da sequência anterior, então podemos reescrevê-la como:

Encontramos o termo geral conforme vimos no exercício anterior e adicionamos + 1.
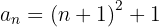
5
A sequência pode ser reescrita como:
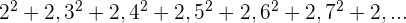
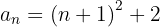
6
A sequência pode ser reescrita como:
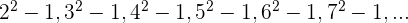
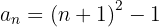
7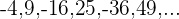
Cada um dos termos desta sequência é o oposto dos termos da sequência  , logo:
, logo:
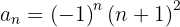
8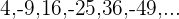
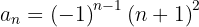
9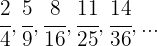
Temos duas sequências, uma para o numerador e outra para o denominador:


A primeira sequência é uma progressão aritmética com  , e a segunda é uma sequência de quadrados perfeitos.
, e a segunda é uma sequência de quadrados perfeitos.
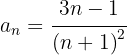
10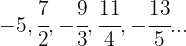
Se ignorarmos o sinal, o numerador é uma progressão aritmética com 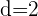 .
.
O denominador é uma progressão aritmética com  .
.
Como os termos ímpares são negativos, multiplicamos 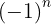 .
.
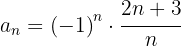
Calcule o termo geral das seguintes sequências
Calcule o termo geral das sequências a seguir:
1
2
3
4
5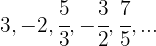
6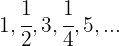
7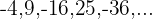
8
9
10
1
O numerador é constante.
O denominador é uma progressão aritmética com  .
.
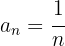
2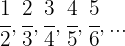
O numerador é uma progressão aritmética com 
O denominador é uma progressão aritmética com 

3
Se escrevemos cada termo da sequência como fração, teríamos:

O numerador é uma progressão aritmética com 
O denominador é uma progressão aritmética com 
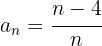
4
Se ignorarmos o sinal, é uma progressão aritmética com 
Como os termos ímpares são negativos, multiplicamos por 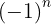
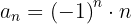
5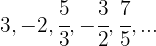
A sequência pode ser reescrita como:
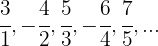
Se ignorarmos o sinal, o numerador é uma progressão aritmética com 
O denominador é uma progressão aritmética com 
Como os termos pares são negativos, multiplicamos por 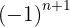
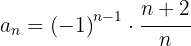
6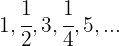
É uma sequência oscilante.
Os termos ímpares formam uma progressão aritmética com  , se não contarmos os termos pares.
, se não contarmos os termos pares.
O denominador dos termos pares forma uma progressão aritmética com 
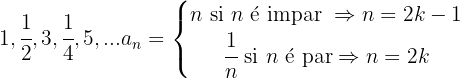
7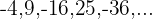
A sequência pode ser reescrita como:

Se ignorarmos o sinal e o expoente, temos uma progressão aritmética com 
Como os termos estão elevados ao quadrado, também temos que elevar o termo geral ao quadrado.
Como os termos ímpares são negativos, multiplicamos por 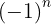
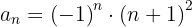
8
A sequência pode ser reescrita como:

É uma sequência oscilante.
O numerador dos termos ímpares forma uma progressão aritmética com  , se não contarmos os termos pares.
, se não contarmos os termos pares.
Como os termos estão elevados ao quadrado, também temos que elevar o termo geral ao quadrado.
O primeiro somatório do denominador (sem contar o quadrado) é uma progressão aritmética com  (sem contar os termos pares).
(sem contar os termos pares).
Elevamos o termo geral ao quadrado e somar + 
Os termos pares formam uma sequência constante.
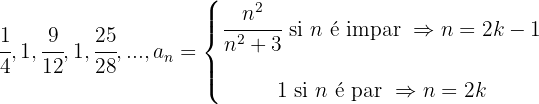
9
Separando as sequências do numerador e do denominador:
Numerador: 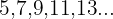
Denominador: 
O numerador é uma progressão aritmética com 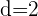
O denominador é uma progressão geométrica com 
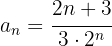
10
Se ignorarmos o sinal, o numerador é uma progressão aritmética com 
O denominador é uma progressão geométrica com 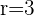
Como os termos pares são negativos, multiplicamos por 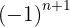
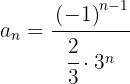
Resumir com IA:












