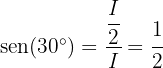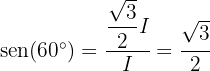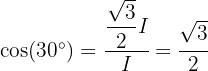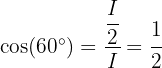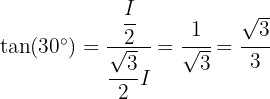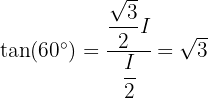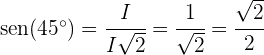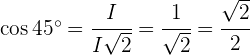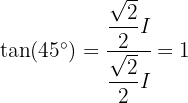Temas
Neste artigo, obteremos os valores exatos das funções trigonométricas - seno, cosseno e tangente - para os ângulos de 30°, 45° e 60°. Estes ângulos fazem parte, juntamente com os ângulos de 0° e 90°, dos bem conhecidos ângulos notáveis.

Seno, cosseno e tangente de 30º e 60º
Para obter o valor das razões trigonométricas seno, cosseno e tangente de 30° e 60°, desenhamos um triângulo equilátero com os vértices A, B e C, conforme mostrado na imagem. Como é um triângulo equilátero, cada um dos seus três ângulos mede 60°. Agora, traçamos a altura h dividindo o vértice A pela metade. O resultado nos dá dois ângulos de 30° cada.
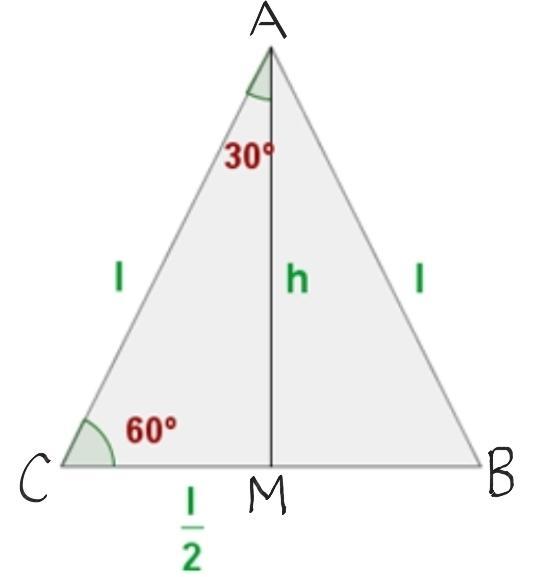
Assim, usando o Teorema de Pitágoras o triângulo retângulo dos vértices AMC, descobriremos que a altura é:

Agora, usando a definição das razões trigonométricas em um triângulo retângulo, sabemos que
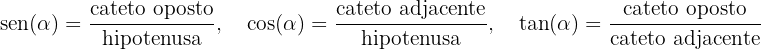
para um ângulo interno  do triângulo, diferente do ângulo reto. Portanto, temos que
do triângulo, diferente do ângulo reto. Portanto, temos que
Seno, cosseno e tangente de 45º
Para obter o valor das funções trigonométricas seno, cosseno e tangente no ângulo de 45°, construímos um quadrado. Cada ângulo interno do quadrado mede 90°. Traçamos a diagonal, a qual divide dois de seus ângulos internos e obtemos ângulos de 45°.

Novamente, utilizando o Teorema de Pitágoras, a referida diagonal tem um comprimento de

De novo, usando a definição das razões trigonométricas em um triângulo retângulo, se obtém que
Razões trigonométricas de ângulos notáveis
Finalmente, podemos resumir toda a informação que apresentamos neste artigo na seguinte tabela, conhecida como a tabela de razões trigonométricas de ângulos notáveis:
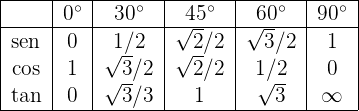
Aqui, para completar a tabela, usamos os conhecidos valores das funções trigonométricas dos ângulos de 0° e 90°:
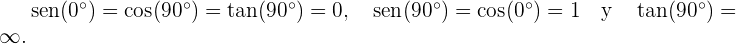
Resumir com IA: