Temas
Dois triângulos são semelhantes quando têm seus ângulos correspondentes iguais e seus lados correspondentes proporcionais.

Definição de semelhança de triângulos
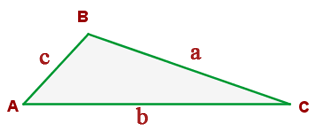
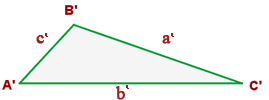
Dados os triângulos  e
e 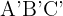 , os lados
, os lados  e
e  ,
,  e
e  ,
,  e
e  são chamados lados correspondentes. Os ângulos correspondentes são:
são chamados lados correspondentes. Os ângulos correspondentes são: 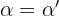 ,
,  e
e 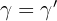 . Dois triângulos são semelhantes quando têm seus ângulos correspondentes iguais e seus lados correspondentes proporcionais, ou seja, quando satisfaz a:
. Dois triângulos são semelhantes quando têm seus ângulos correspondentes iguais e seus lados correspondentes proporcionais, ou seja, quando satisfaz a:
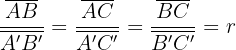
e

A razão da proporção  , entre os lados correspondentes dos triângulos é chamada razão de semelhança.
, entre os lados correspondentes dos triângulos é chamada razão de semelhança.
Observações:
1. A razão entre os perímetros de triângulos semelhantes é igual à razão de semelhança.
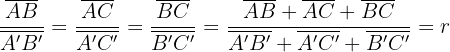
2. A razão entre as áreas de triângulos semelhantes é igual ao quadrado da razão de semelhança. Assim, se as áreas dos triângulos  e
e 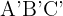 são
são  e
e 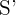 , respectivamente, então:
, respectivamente, então:
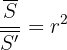
Exemplos práticos
1 Calcule a altura de um edifício que projeta uma sombra de 6,5 m no mesmo instante em que um poste de 4,5 m de altura projeta uma sombra de 0,90 m.
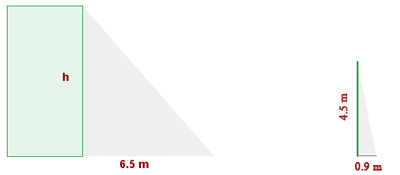
Como as sombras são projetadas ao mesmo tempo, podemos supor que há semelhança para resolver o problema. Assim, pela semelhança, temos a igualdade:

isolando  obtemos:
obtemos:
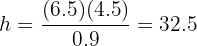
2 Os catetos de um triângulo retângulo medem 24 m e 10 m. Quanto medirão os catetos de um triângulo semelhante ao primeiro, cuja hipotenusa mede 52 m?
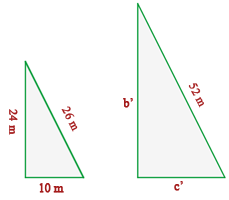
Como temos os catetos de um dos triângulos retângulos, podemos calcular sua hipotenusa:
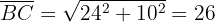
Sabendo a hipotenusa e que os triângulos são semelhantes, usaremos o fato de que os lados são proporcionais para determinar os catetos do outro triângulo. Primeiro, vamos calcular:


isolando  obtemos:
obtemos:
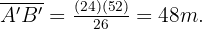
Agora, vamos calcular: 
isolando  obtemos:
obtemos:

Critérios de semelhança
Ângulos iguais
Dois triângulos são semelhantes se têm dois ângulos iguais.
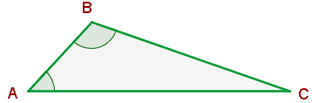
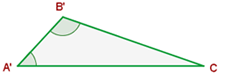
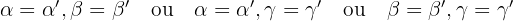
Lados proporcionais
Dois triângulos são semelhantes se têm os lados proporcionais.
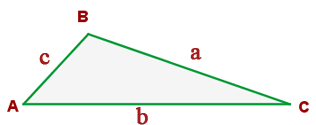
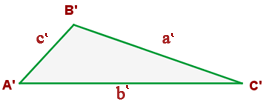
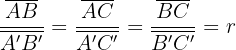
Ângulo entre lados
Dois triângulos são semelhantes se têm dois lados proporcionais e o ângulo compreendido entre eles igual.
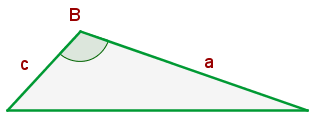
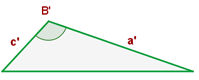
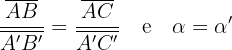
ou
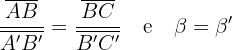
ou
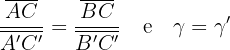
Exercícios sobre semelhança de triângulos
Verifique se os seguintes triângulos são semelhantes:
1
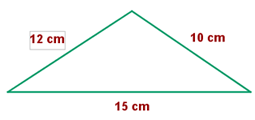
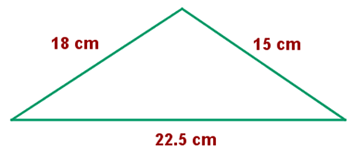
Neste exemplo, analisaremos se os lados são proporcionais. Para isso, podemos proceder de diferentes formas. O que faremos é reduzir cada razão de lados à sua forma mais simples e verificar se elas coincidem. Se coincidirem, teremos encontrado a razão de semelhança  . Assim:
. Assim:
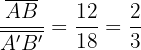 ,
,
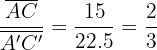 ,
,
E, por fim,
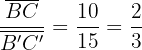 .
.
Portanto,

Concluímos que os triângulos são semelhantes porque possuem lados proporcionais.
2
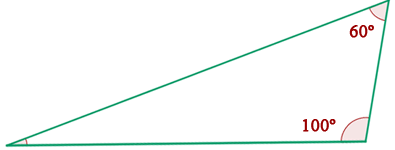
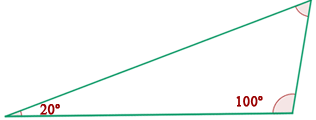
Recordemos que a soma dos ângulos internos de um triângulo é sempre  . Assim:
. Assim:
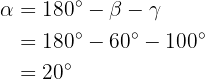
Notamos que  e
e  . Logo, os triângulos são semelhantes porque possuem dois ângulos iguais.
. Logo, os triângulos são semelhantes porque possuem dois ângulos iguais.
3
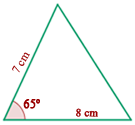
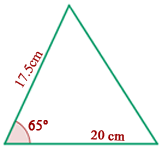
Vamos verificar se os dois lados dados em cada triângulo são proporcionais e se o ângulo entre eles é igual. Primeiro, vemos que  .
.
Falta apenas verificar a proporcionalidade dos lados:
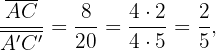
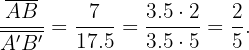
Portanto:

Assim, os triângulos são semelhantes porque têm dois lados proporcionais e os ângulos compreendidos entre eles iguais.
Semelhança de triângulos retângulos
Ângulo
Dois triângulos retângulos são semelhantes se têm um ângulo (diferente do ângulo reto) igual.
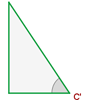
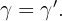
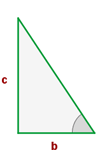
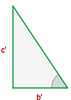
Catetos proporcionais
Dois triângulos retângulos são semelhantes se tiverem os dois catetos proporcionais.

Hipotenusa e cateto
Dois triângulos retângulos são semelhantes se têm a hipotenusa e um cateto proporcionais.
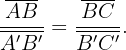
Resumir com IA:












