Temas

Unidade imaginária
Chama-se unidade imaginária o número 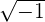 , que é representado pela letra
, que é representado pela letra  .
.
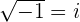
A raiz cúbica de  não é um número imaginário nem complexo.
não é um número imaginário nem complexo.
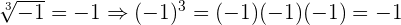
Exemplos com a unidade imaginária
1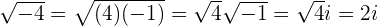
2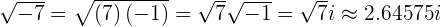
3
4 
Número complexo
O número 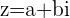 é chamado de número complexo na forma algébrica (ou binômica). Em geral, qualquer número complexo é representado pela letra
é chamado de número complexo na forma algébrica (ou binômica). Em geral, qualquer número complexo é representado pela letra  .
.
O número  é chamado de parte real do número complexo e é indicado por
é chamado de parte real do número complexo e é indicado por 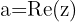 , enquanto o número
, enquanto o número  é chamado de parte imaginária e é indicado por
é chamado de parte imaginária e é indicado por 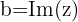 .
.
Se a parte imaginária de um número complexo for zero, isto é,  , o número se reduz a um número real
, o número se reduz a um número real  , pois
, pois 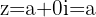 .
.
Se a parte real de um número complexo for zero, isto é, 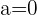 , o número complexo se reduz a
, o número complexo se reduz a  , sendo chamado de número imaginário puro.
, sendo chamado de número imaginário puro.
O conjunto de todos os números complexos é representado por 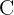 . De forma mais formal:
. De forma mais formal:
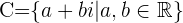
Os números complexos 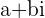 e
e 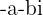 são chamados de opostos.
são chamados de opostos.
Os números complexos 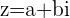 e
e  são chamados de conjugados.
são chamados de conjugados.
Dois números complexos são iguais quando possuem a mesma parte real e a mesma parte imaginária, ou seja:

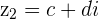
com  ou
ou 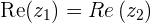 e
e  ou
ou 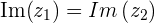
Representação gráfica dos números complexos
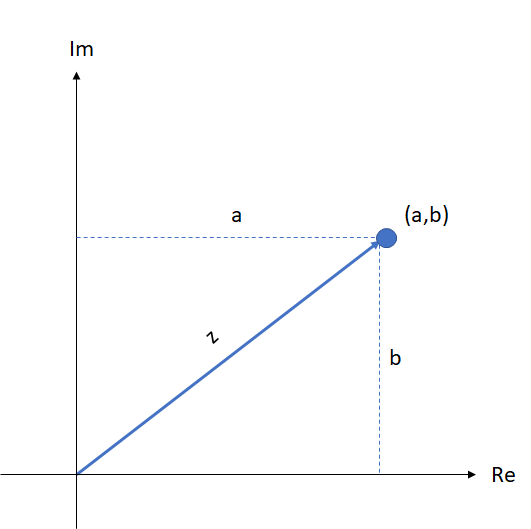
Os números complexos são representados no plano cartesiano, chamado de plano complexo  , na forma de vetor posição, cujo ponto inicial é a origem e o ponto final é o ponto
, na forma de vetor posição, cujo ponto inicial é a origem e o ponto final é o ponto  , chamado de afixo do número complexo.
, chamado de afixo do número complexo.
O eixo  é chamado de eixo real e o eixo
é chamado de eixo real e o eixo  , de eixo imaginário.
, de eixo imaginário.
O plano complexo também é conhecido como plano de Argand-Gauss.
Potências de unidade imaginária

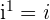
 , pois
, pois 
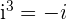 , pois
, pois 
 , pois
, pois  ou
ou 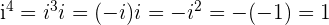
Exemplos de potências maiores de números complexos
1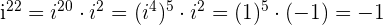
2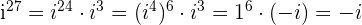
3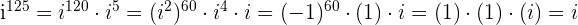
4
Números imaginários puros
Un número imaginario puro é dado por:
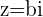
onde:
 é um número real.
é um número real.
 é a unidade imaginária.
é a unidade imaginária.
Lembrando que sua parte real é  , isto é,
, isto é, 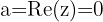 . Quando a parte real é diferente de zero, o número passa a ter parte real e parte imaginária e, portanto, é classificado como número complexo, e não apenas como número imaginário.
. Quando a parte real é diferente de zero, o número passa a ter parte real e parte imaginária e, portanto, é classificado como número complexo, e não apenas como número imaginário.
Operações com números complexos na forma algébricaSoma e subtração de números complexos
A regra para somar ou subtrair dois números complexos 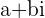 e
e  é somar ou subtrair a parte real de um com a parte real do outro e a parte imaginária de um com a parte imaginária do outro.
é somar ou subtrair a parte real de um com a parte real do outro e a parte imaginária de um com a parte imaginária do outro.
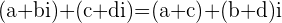

Quando aparecem somas e subtrações combinadas envolvendo vários números complexos, somam-se e/ou subtraem-se as partes reais entre si e as partes imaginárias entre si.
Exemplos:
1
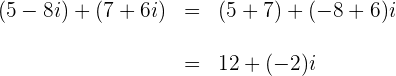
2

3
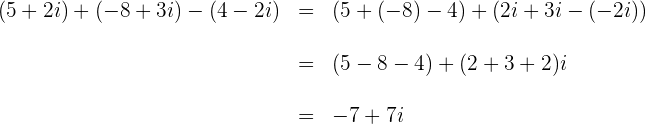
A soma e a subtração de números complexos também podem ser feitas da mesma forma que a soma e a subtração de polinômios, pois os números complexos estão escritos na forma algébrica.
Exemplo:

Produto de números complexos
O produto, ou multiplicação, de números complexos escritos na forma algébrica é feito de acordo com a seguinte fórmula:
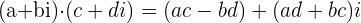
ou
Esse produto também pode ser realizado como a multiplicação de dois binômios.
Exemplo de acordo com a fórmula:

Exemplo como produto de binômios:
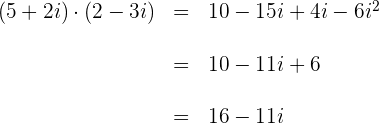
Quociente de números complexos
A divisão de dois números complexos escritos na forma de fração é feita multiplicando-se tanto o numerador quanto o denominador pelo conjugado do denominador. Em seguida, realizam-se as simplificações necessárias até que o resultado fique escrito na forma algébrica:
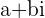 .
.
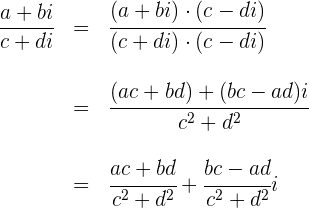
Exemplos:
1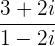
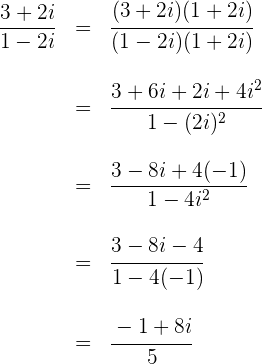
2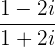
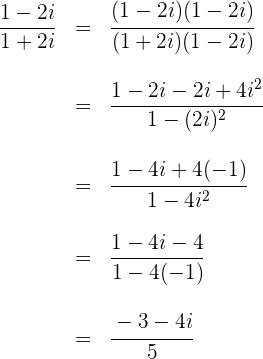
Módulo e argumento de números complexos
O módulo de um número complexo (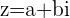 ), quando representado graficamente, corresponde ao comprimento do vetor que vai da origem até o seu afixo, ou ponto final
), quando representado graficamente, corresponde ao comprimento do vetor que vai da origem até o seu afixo, ou ponto final . O módulo é indicado por:
. O módulo é indicado por:
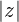 .
.
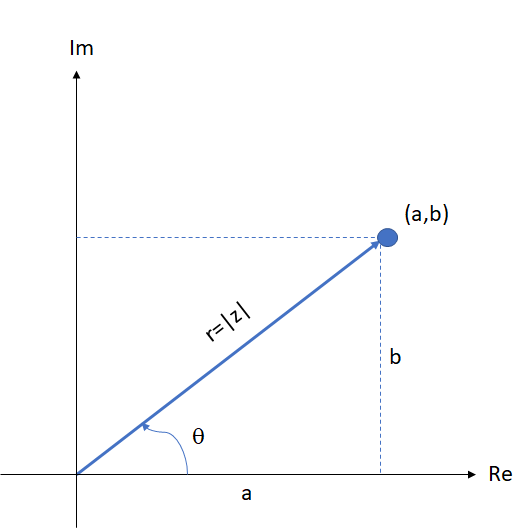
Aplicando o Teorema de Pitágoras ao triângulo 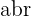 da figura, obtém-se a fórmula para calcular o módulo de um número complexo:
da figura, obtém-se a fórmula para calcular o módulo de um número complexo:
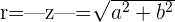
O argumento de um número complexo é o ângulo positivo, medido no sentido anti-horário, que o vetor forma com a parte positiva do eixo real. Ele é indicado por 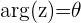 e é calculado por meio das fórmulas a seguir, de acordo com o quadrante em que o número complexo se encontra.
e é calculado por meio das fórmulas a seguir, de acordo com o quadrante em que o número complexo se encontra.
Primeiro quadrante
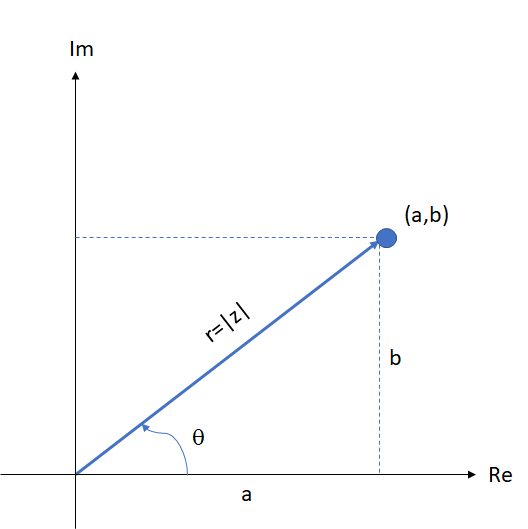
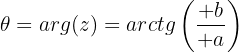
Segundo quadrante
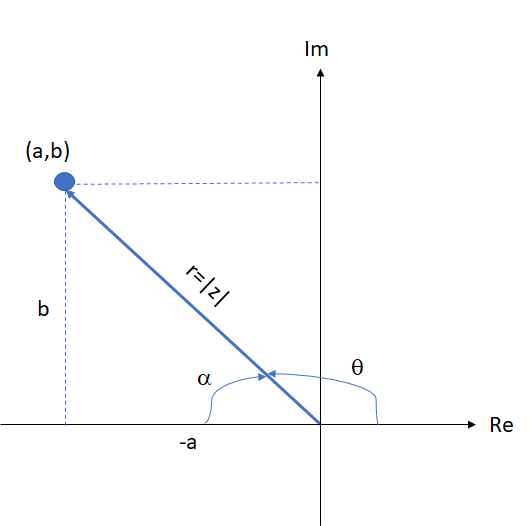
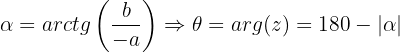
Terceiro quadrante
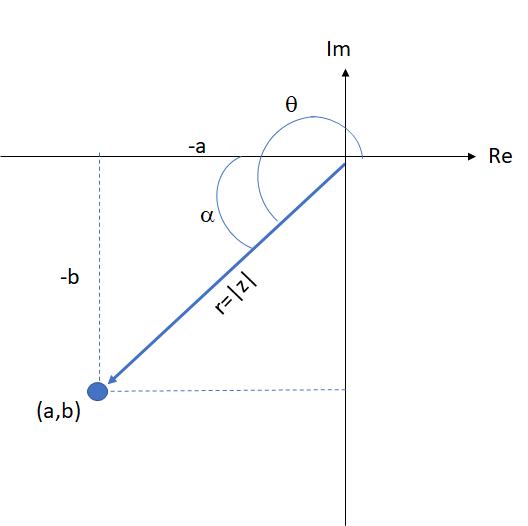
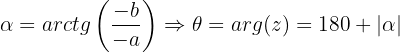
Quarto quadrante
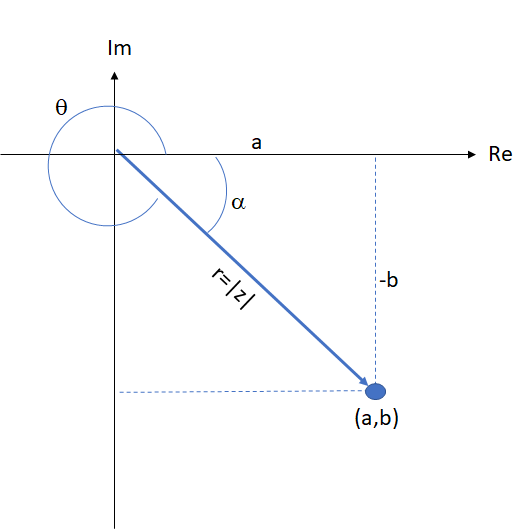
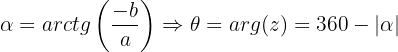
Exemplos: Vamos calcular o módulo e o argumento dos seguintes números complexos e também fazer sua representação gráfica.
1 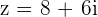
Calculamos o módulo:

Calculamos o argumento:
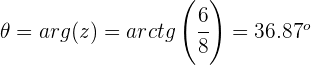
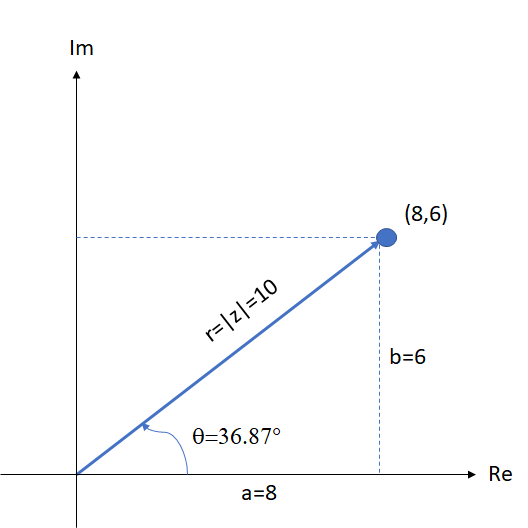
Representação gráfica:
2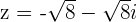
Calculamos o módulo:
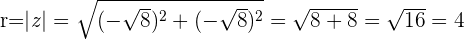
Calculamos o argumento:
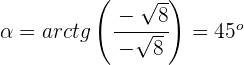
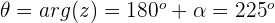
Representação gráfica:
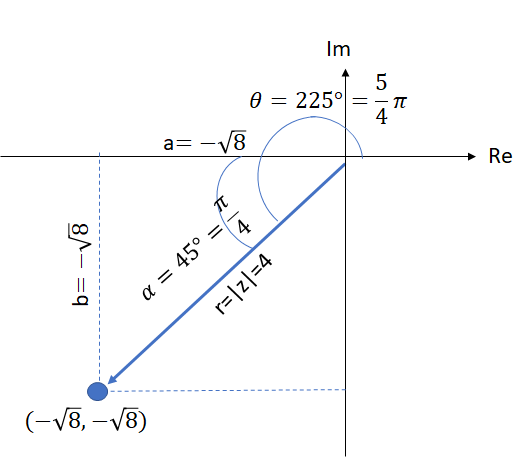
Números complexos em forma trigonométrica ou polar
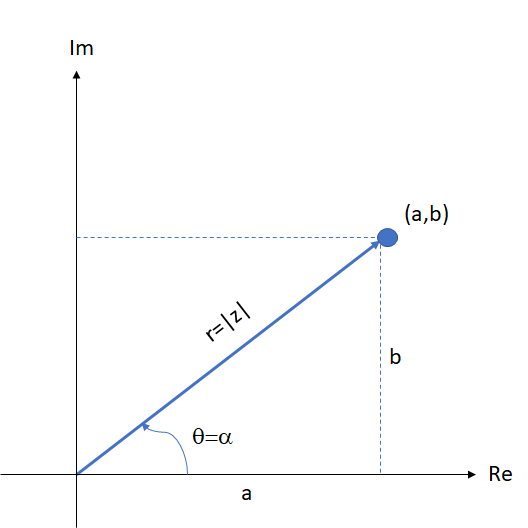
Para obter as partes real e imaginária,  e
e  , respectivamente, de um número complexo em função do seu módulo e do seu argumento, aplicam-se as definições das funções seno e cosseno do ângulo
, respectivamente, de um número complexo em função do seu módulo e do seu argumento, aplicam-se as definições das funções seno e cosseno do ângulo  , no triângulo
, no triângulo 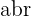 da figura anterior.
da figura anterior.

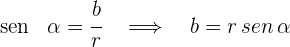
Posteriormente, la forma trigonométrica y polar del número completo se expresa así:

Na tabela abaixo, estão os resumos das formas algébrica ou binômica, polar e trigonométrica de qualquer número complexo.
| Algébrica (binômica) | 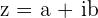 |
|---|---|
| Polar | 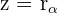 |
| Trigonométrica | 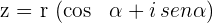 |
Números complexos iguais, conjugados e opostos nas formas trigonométrica e polar
O gráfico a seguir mostra a representação, tanto na forma polar quanto na forma trigonométrica, de um número complexo 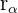 , do seu complexo conjugado
, do seu complexo conjugado 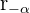 e do seu complexo oposto
e do seu complexo oposto 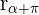 .
.
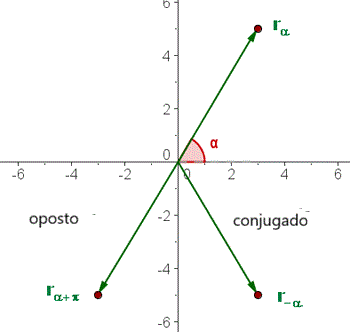
Números Complexos Iguais

Números Complexos Conjugados


Números Complexos Opostos


Produto de números complexos na forma polar
Fórmula

Exemplos:
1

2

Produto por um número complexo de módulo 1
Al multiplicar un número complejo 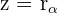 por
por  se gira
se gira  un ángulo
un ángulo  alrededor del origen.
alrededor del origen.
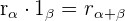
Quociente de números complexos na forma polar
Fórmula:

Exemplos:
1

2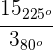
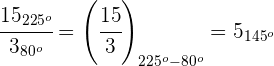
Potência de números complexos na forma polar
Fórmula:

Exemplos:
1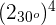
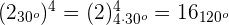
2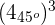

Fórmula de Moivre
O Teorema de Moivre é utilizado para calcular potências inteiras positivas de números complexos escritos na forma trigonométrica.
A fórmula de Moivre é:
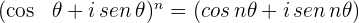
Se aplicarmos à  -ésima potência de um número complexo escrito na forma polar:
-ésima potência de um número complexo escrito na forma polar:
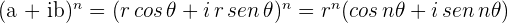
Exemplo:
Vamos calcular a potência do seguinte número complexo, escrito na forma algébrica (binômica), usando a forma trigonométrica e o Teorema de Moivre, já que fazer pela expansão binomial seria mais demorado e trabalhoso.

Passo 1. Calcula-se o módulo e o argumento da base da potenciação, que é o número complexo sem expoente.
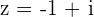
Módulo:

Argumento:
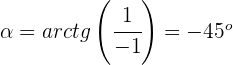
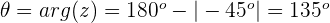
Passo 2. Expressa-se o número complexo na sua forma trigonométrica
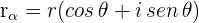

Passo 3. Aplica-se a fórmula de Moivre.

Paso 4. Escreve-se o resultado sem o procedimento.

Raiz n-ésima de números complexos na forma polar
Todo número complexo (exceto o zero) possui exatamente  raízes n-ésimas distintas.
raízes n-ésimas distintas.
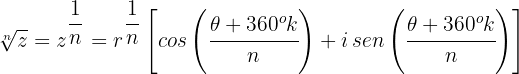

Exemplo:

Passo 1. Calculam-se o módulo e o argumento do número complexo do qual se está extraindo a raiz sexta.

Módulo
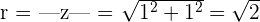
Argumento
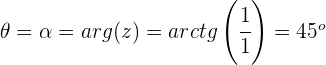
Paso 2. Substituem-se os dados na fórmula para calcular as 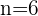 raízes n-ésimas do número complexo
raízes n-ésimas do número complexo 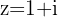 .
.
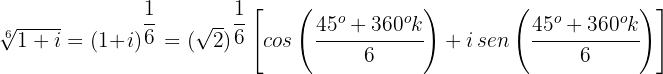
Paso 3. Varia-se o valor de  de
de 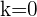 até
até 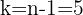 para obter as
para obter as  raízes n-ésimas de
raízes n-ésimas de 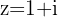 .
.
Para 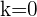
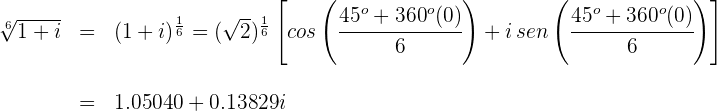
Para 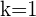

Para 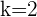

Para 
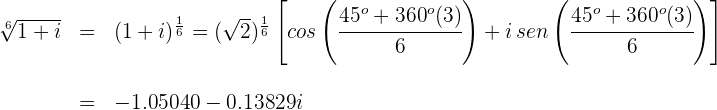
Para 
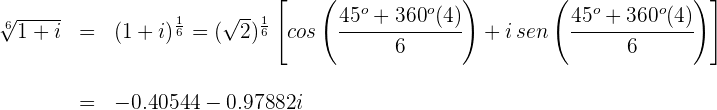
Para 
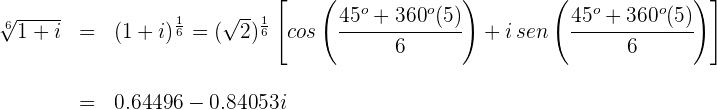
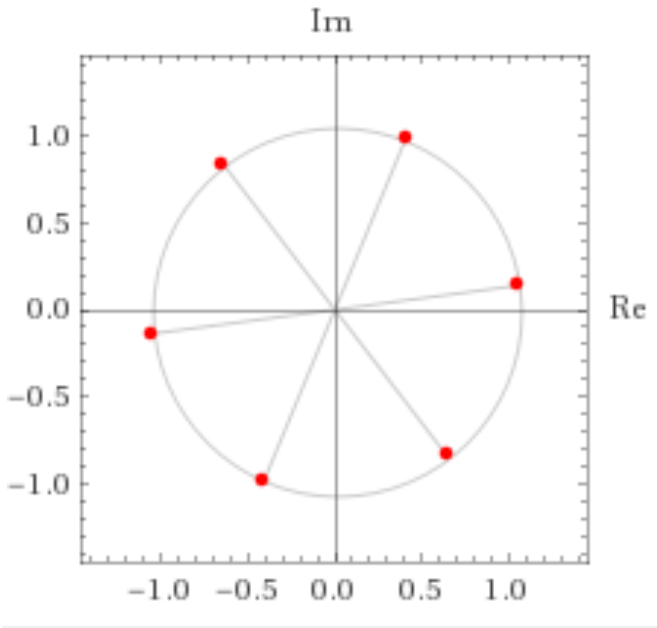
Representação gráfica das  raízes do número complexo
raízes do número complexo 
Resumir com IA:












