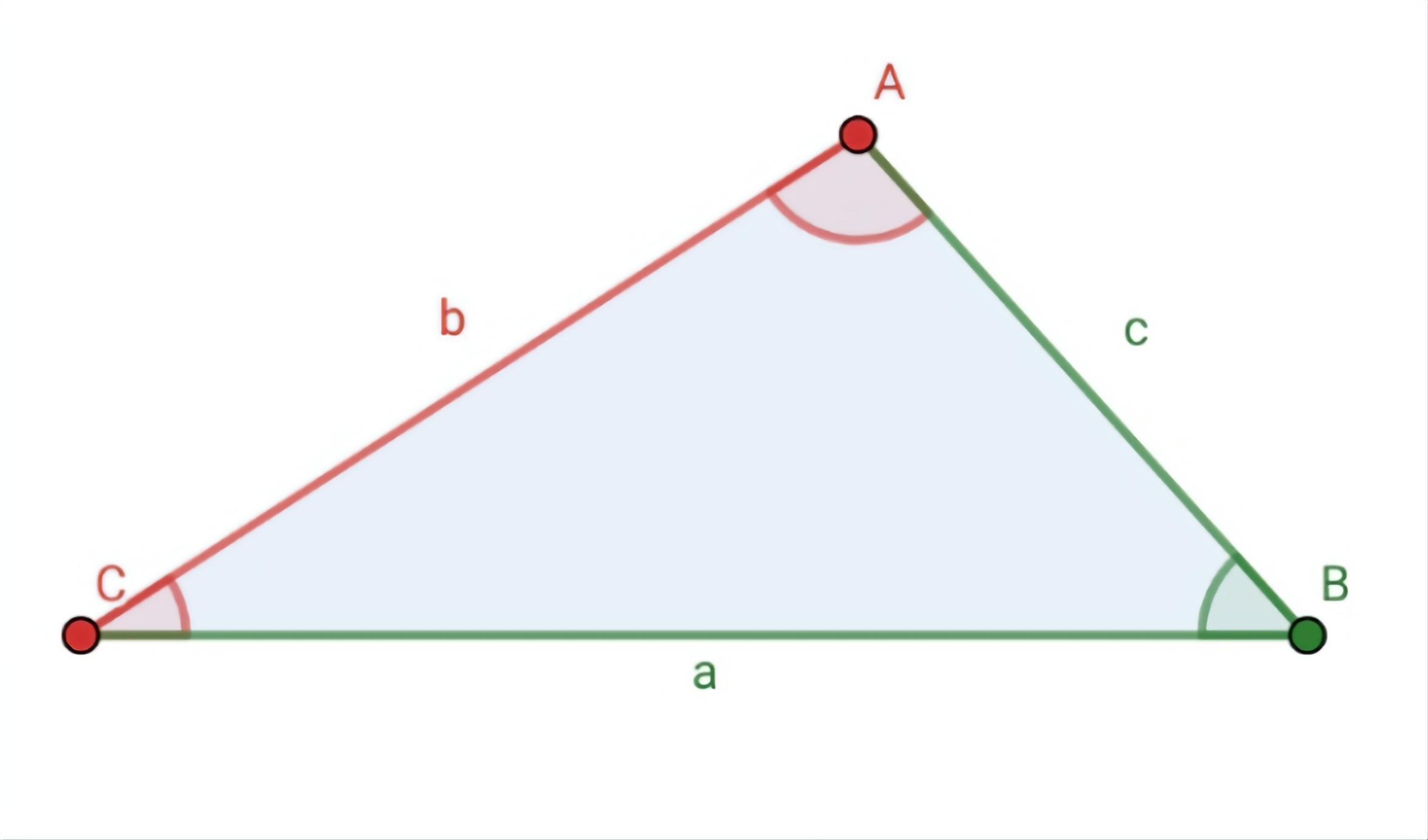
Seja bem-vindo à nossa página dedicada a exercícios de resolução de triângulos! Alguma vez você já se perguntou como determinar o comprimento de um lado desconhecido de um triângulo? Ou como encontrar aqueles ângulos ocultos que desafiam a sua intuição? Nosso objetivo é fornecer as ferramentas e técnicas necessárias para resolver esses quebra-cabeças geométricos com facilidade.
Nos acompanhe na exploração dos diferentes métodos para resolver triângulos, desde o clássico Teorema de Pitágoras até as sofisticadas Leis dos Senos e Cossenos. Além disso, vamos aprender sobre triângulos especiais e suas propriedades únicas, e como aplicar essas informações em situações do mundo real.
Temos certeza de que esta série de exercícios que desenvolvemos para você será útil para se tornar um verdadeiro especialista na resolução de triângulos. Partiu!
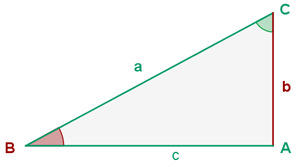
De um triângulo retângulo  , sabemos que
, sabemos que  e
e 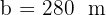 . Resolva o triângulo.
. Resolva o triângulo.
1. Veja essa expressão do seno do ângulo 
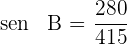
Aplicamos a função  a ambos os lados da equação e se obtém
a ambos os lados da equação e se obtém

2. O ângulo 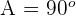 . Calculamos o ângulo
. Calculamos o ângulo 
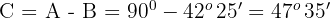
3. Para calcular o lado  usamos a função cosseno para o ângulo
usamos a função cosseno para o ângulo 
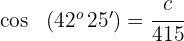
Isolamos  e resolvemos
e resolvemos
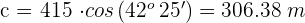
De um triângulo retângulo  , se sabe
, se sabe  e
e 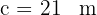 . Resolva o triângulo.
. Resolva o triângulo.

1. Expressamos a tangente do ângulo 

Aplicamos a função  a ambos os lados da equação e se obtém
a ambos os lados da equação e se obtém

2. O ângulo 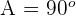 . Calculamos o ângulo
. Calculamos o ângulo 
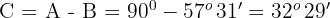
3. Para calcular o lado  Usamos a função seno para o ângulo.
Usamos a função seno para o ângulo. 
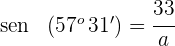
Isolamos  e resolvemos
e resolvemos
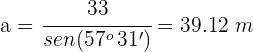
De um triângulo retângulo  , se sabe
, se sabe 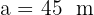 e
e  . Resolva o triângulo.
. Resolva o triângulo.

1. O ângulo 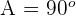 . Calculamos o ângulo
. Calculamos o ângulo 
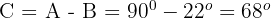
2. Expressamos o seno do ângulo 
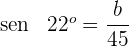
Isolamos  e resolvemos
e resolvemos
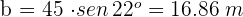
3. Para calcular o lado  usamos a função cosseno para o ângulo.
usamos a função cosseno para o ângulo. 
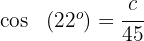
Isolamos  e resolvemos
e resolvemos
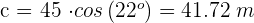
De um triângulo retângulo  , é conhecido
, é conhecido  e
e 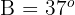 . Resolva o triângulo
. Resolva o triângulo

1. O ângulo 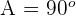 . Calculamos o ângulo
. Calculamos o ângulo 
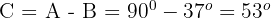
2. Expressamos o seno do ângulo 

Isolamos  e resolvemos
e resolvemos
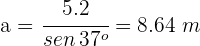
3. Para calcular o lado  usamos a função tangente para o ângulo.
usamos a função tangente para o ângulo. 
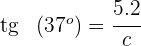
Isolamos  e resolvemos
e resolvemos

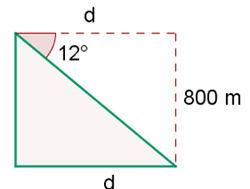
Um dirigível que está voando a  de altura, avista uma cidade com um ângulo de depressão de
de altura, avista uma cidade com um ângulo de depressão de  . Qual a distância que o dirigível se encontra da cidade?
. Qual a distância que o dirigível se encontra da cidade?
1. Vamos representar os dados informados em um gráfico
2. Fazemos a expressão da tangente do ângulo 

Isolamos a distância  e resolvemos
e resolvemos
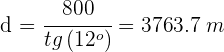
Encontre o raio de uma circunferência sabendo que uma corda de 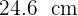 tem um arco correspondente de
tem um arco correspondente de 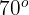 .
.
1. Vamos representar os dados informados através de um gráfico
2. Forma-se um triângulo isósceles, cujos lados iguais correspondem ao raio da circunferência. Consideramos  o ponto médio do segmento
o ponto médio do segmento  , assim, o triângulo
, assim, o triângulo  é retângulo e
é retângulo e 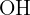 dividindo o ângulo em duas partes iguais
dividindo o ângulo em duas partes iguais 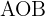
3. Calculamos o seno do ângulo 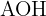
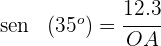
Isolamos a distância  e resolvemos
e resolvemos
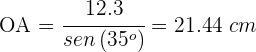
Desta forma, o raio que estamos buscando é 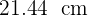 .
.
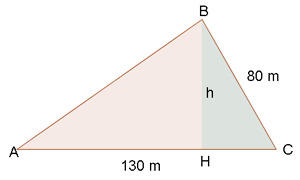
Calcule a área de um triângulo, sabendo que dois de seus lados medem 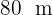 e
e 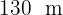 , e formam entre si um ângulo de
, e formam entre si um ângulo de 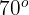 .
.
1. Vamos representar através de um gráfico os dados informados
2. Calculamos a altura  do triângulo, para isso, calculamos o seno de
do triângulo, para isso, calculamos o seno de 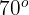
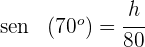
3. Isolamos  e resolvemos
e resolvemos

A área solicitada é
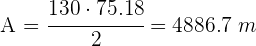
Calcule a altura de uma árvore, sabendo que de um ponto no terreno sua copa é observada sob um ângulo de 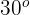 e ao nos aproximar
e ao nos aproximar  , o ângulo passa a ser de
, o ângulo passa a ser de 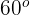 .
.
1. Vamos registrar as informações disponíveis em um gráfico
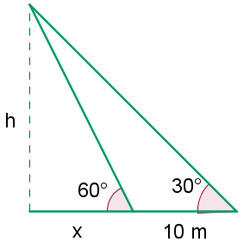
2. Calculamos a tangente de 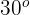 e isolamos
e isolamos 

3. Calculamos a tangente de 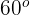 e isolamos
e isolamos 
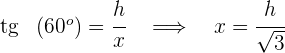
Igualamos ambos valores de  e temos o resultado em
e temos o resultado em 
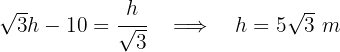
O comprimento do lado de um octógono regular é  . Determine os raios da circunferência inscrita e circunscrita.
. Determine os raios da circunferência inscrita e circunscrita.
1. Vamos organizar os dados informados em um gráfico
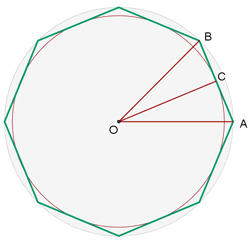
2. O ângulo 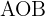 é igual a
é igual a 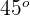 , no qual, o ângulo
, no qual, o ângulo  é igual a
é igual a  . Para calcular o raio da circunferência inscrita, vamos usar
. Para calcular o raio da circunferência inscrita, vamos usar
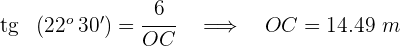
3. Para calcular el raio da circunferência circunscrita, vamos utilizar

Calcule o comprimento do lado e da apótema de um octógono regular inscrito em uma circunferência de 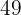 centímetros de raio.
centímetros de raio.
1. Vamos representar, em um gráfico, os dados disponíveis
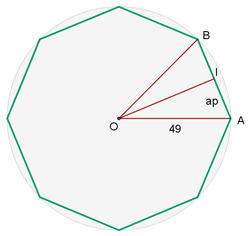
2. O ângulo 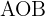 é igual a
é igual a 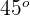 , assim, se traçamos a bissetriz, por se tratar de um triângulo isósceles, obtemos dois triângulos retângulos iguais. Para calcular o lado, usamos
, assim, se traçamos a bissetriz, por se tratar de um triângulo isósceles, obtemos dois triângulos retângulos iguais. Para calcular o lado, usamos

3. Para calcular o apótema utilizamos
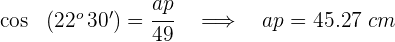
Três cidades A, B e C são unidas por rodovias. A distância de A a C é  km e a de B a C é
km e a de B a C é  km. O ângulo que formam estas rodovias é de
km. O ângulo que formam estas rodovias é de  . Qual a distância entre A e B?
. Qual a distância entre A e B?
1. Vamos organizar as informações dos dados do problema e construir um  de modo que
de modo que  se encontre no segmento
se encontre no segmento 

2. Vamos calcular a altura
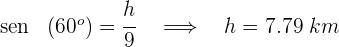
3. Calculamos a distância 
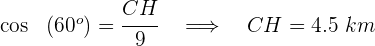
4. Vamos calcular a distância  usando o teorema de Pitágoras
usando o teorema de Pitágoras
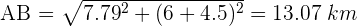
De um triângulo  , se sabe
, se sabe 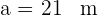 ,
,  e
e 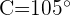 . Resolva o triângulo.
. Resolva o triângulo.
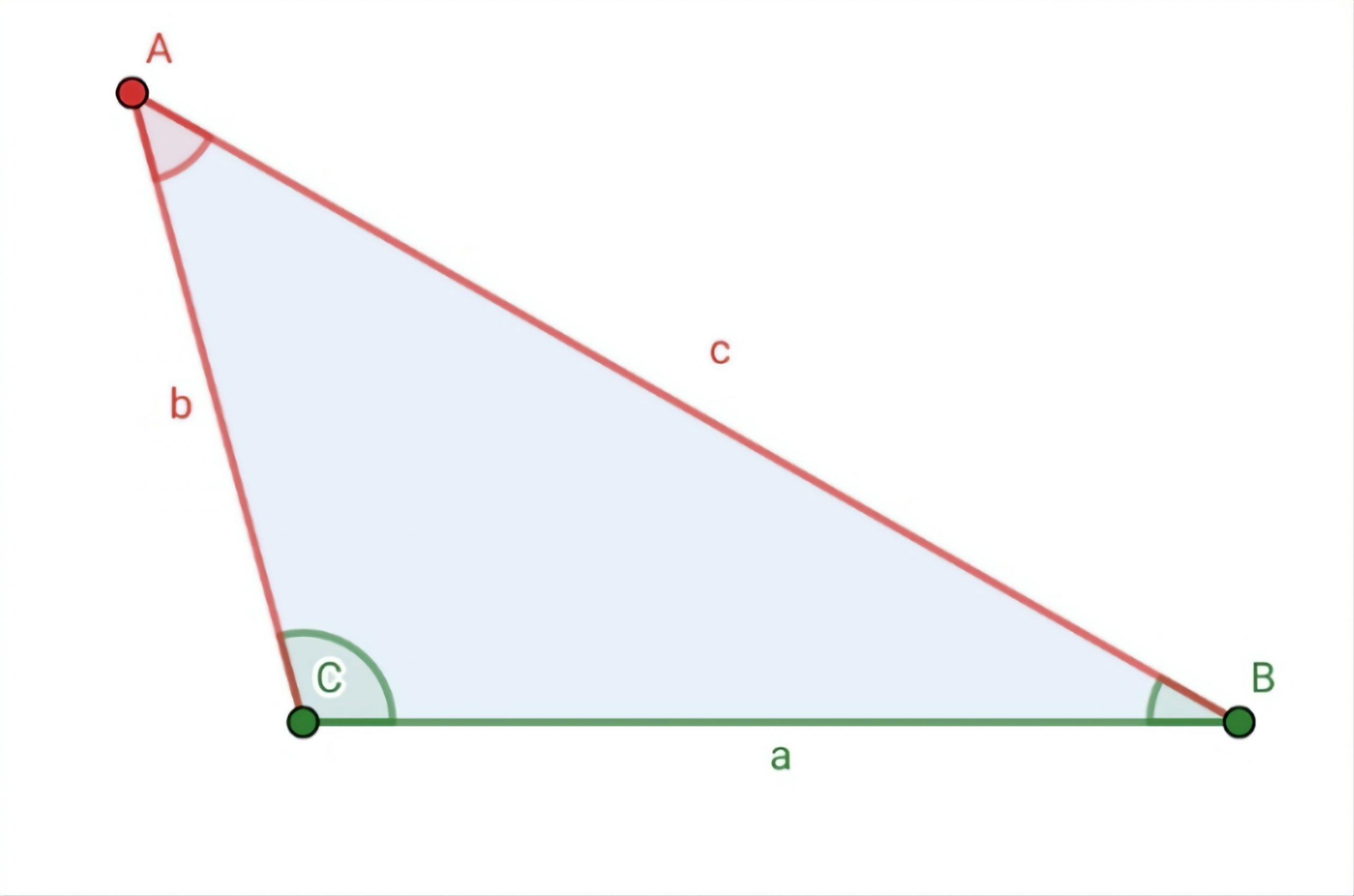
Para resolver o triângulo, devemos encontrar os valores do ângulo  e dos lados
e dos lados  e
e  .
.
Para encontrar o ângulo restante, utilizamos que

Dessa forma,

Para encontrar os lados que faltam do triãngulo, utilizamos o Teorema do seno:

Ou seja,

Da mesma maneira,

Do triângulo  , se sabe
, se sabe 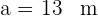 ,
,  e
e  . Resolve o triângulo.
. Resolve o triângulo.
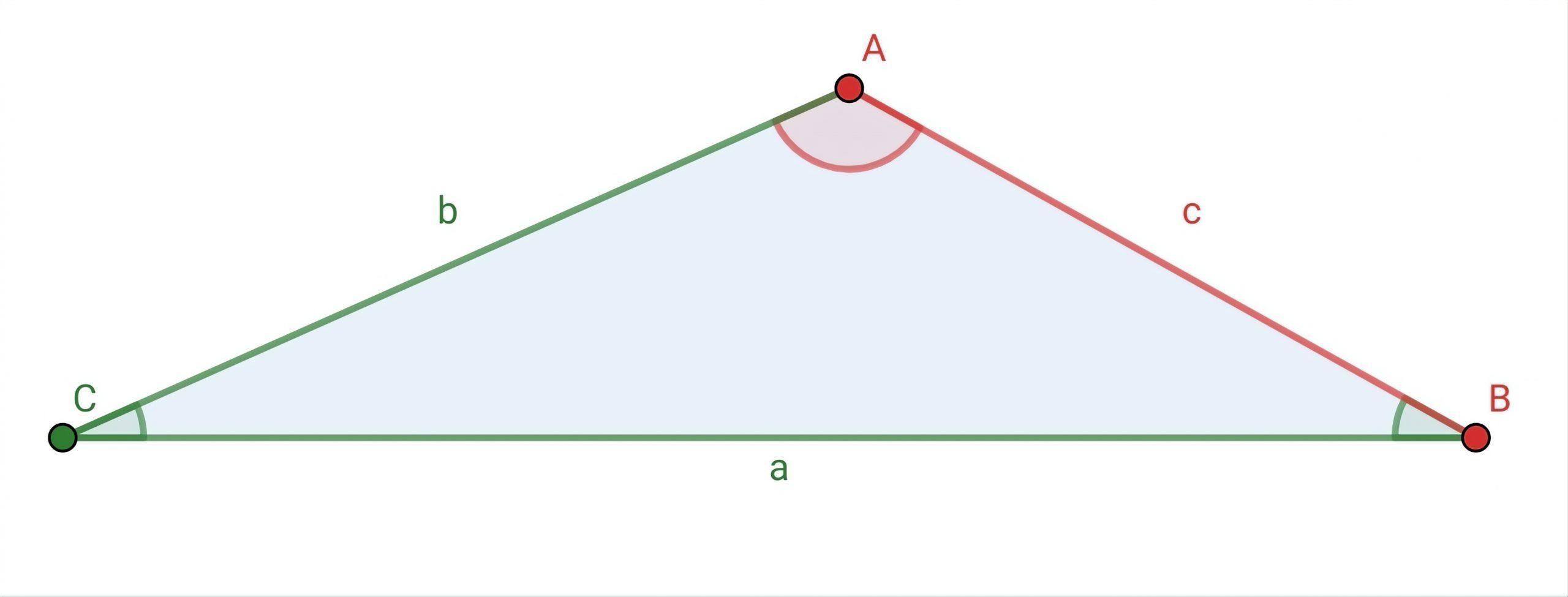
Para resolver o triângulo, devemos encontrar o valor do lado  e dos ângulos
e dos ângulos  e
e  .
.
Para encontrar o outro ángulo restante, vamos utilizar o Teorema do cosseno:
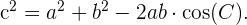
Assim,
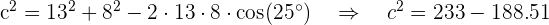
Assim,
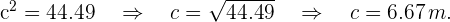
Para encontrar os ângulos, novamente utilizamos o Teorema do cosseno:
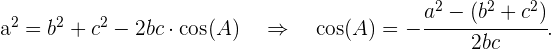
Assim,
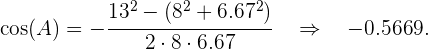
Portanto,

Por fim, se
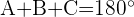
então
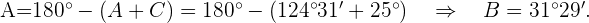
De um triângulo retângulo  , é informado que
, é informado que 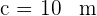 e
e 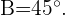 Calcule a área dele
Calcule a área dele
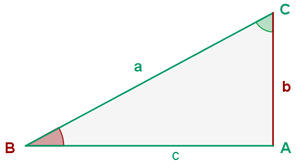
Para calcular a área primeiro, vamos encontrar a base e a altura do triângulo, que neste caso correspondem aos lados  e
e  .
.
Temos que 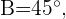 assim
assim

Por outro lado, também sabemos que
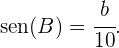
Com isso, podemos entender que
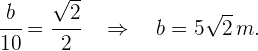
Do Teorema de Pitágoras se extrai que
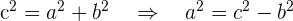
O que implica que
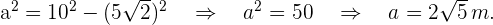
Finalmente, a área do triângulo é
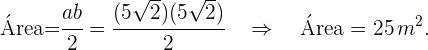
De um triângulo  , se sabe
, se sabe  ,
, 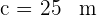 e
e  . Calcule a área.
. Calcule a área.
Para calcular a área do triângulo, utilizamos a fórmula

Sendo assim,
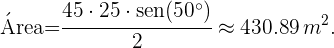
Resumir com IA:


