Um vetor  possui os componentes
possui os componentes 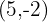 . Encontre as coordenadas de
. Encontre as coordenadas de  sabendo que o extremo
sabendo que o extremo  .
.
Um vetor  possui os componente
possui os componente 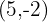 . Encontre as coordenadas de
. Encontre as coordenadas de  sabendo que o extremo
sabendo que o extremo  .
.
1. Como não conhecemos as coordenadas de  , vamos expressá-las mediante:
, vamos expressá-las mediante:
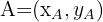 .
.
2. Sabemos que as coordenadas de um vetor são obtidas ao diminuirmos o ponto inicial com o ponto final:
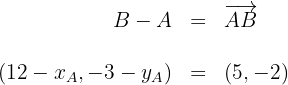
3. Obtemos duas equações:
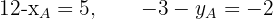
4. Resolvemos as duas equações e chegamos a conclusão que as coordenadas de  são:
são:
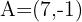
Dado o vetor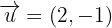 e dois vetores equipolentes a
e dois vetores equipolentes a  e
e 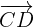 , determine
, determine  e
e  sabendo que
sabendo que 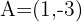 e
e  .
.
Dado o vetor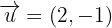 e dois vetores equipolentes a
e dois vetores equipolentes a  y
y 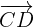 , determine
, determine  e
e  sabendo que
sabendo que 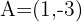 e
e  .
.
1. Como  são equipolentes, portanto
são equipolentes, portanto 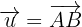 .
.
2. Como não conhecemos as coordenadas de  , vamos expressá-las mediante:
, vamos expressá-las mediante:
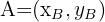 .
.
3. Sabemos que as coordenadas de um vetor são obtidas ao diminuirmos o ponto inicial com o ponto final:
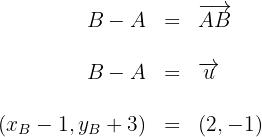
4. Obtemos duas equações:

5. Resolvemos as duas equações e chegamos a conclusão de que as coordenadas de  são:
são:

6 Resolvendo da mesma maneira com  , concluímos que
, concluímos que  .
.
Calcule a distância entre os pontos 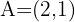 e
e 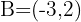 .
.
Calcule a distância entre os pontos 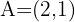 e
e 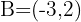 .
.
1. A fórmula para a distância entre dois pontos é:

2. Substituímos os valores de  e
e  na fórmula de distância entre dois pontos e obtemos:
na fórmula de distância entre dois pontos e obtemos: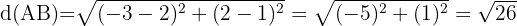
Se  é um vetor com componentes
é um vetor com componentes 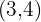 , encontre um vetor unitário com mesma direção e sentido.
, encontre um vetor unitário com mesma direção e sentido.
Se  é um vetor com componentes
é um vetor com componentes 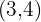 , encontre um vetor unitário com mesma direção e sentido.
, encontre um vetor unitário com mesma direção e sentido.
1. A fórmula para que um vetor seja unitário é: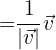
2. Calculamos a magnitude de 

3. Substituímos na fórmula para obtermos um vetor unitário:
Encontre um vetor unitário com mesma direção que o vetor 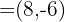 .
.
Encontre um vetor unitário com mesma direção que o vetor 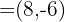 .
.
1. A fórmula para que um vetor seja unitário é: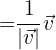
2. Calculamos a magnitude de 

3. Substituímos na fórmula para obtermos um vetor unitário:
Calcule as coordenadas de 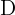 para que o quadrilátero dos vértices
para que o quadrilátero dos vértices  e
e 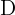 seja um paralelogramo.
seja um paralelogramo.
Calcule as coordenadas de 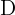 para que o quadrilátero dos vértices
para que o quadrilátero dos vértices  e
e 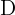 seja um paralelogramo.
seja um paralelogramo.
1. Os lados opostos de um paralelogramo são iguais em magnitude e direção, assim temos
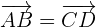
2. Como não conhecemos as coordenadas de 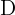 , vamos expressá-las mediante
, vamos expressá-las mediante
 .
.
3. Substituímos os valores dos vértices do paralelogramo com a igualdade dos vetores
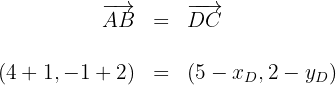
4. Obtemos duas equações

5. Resolvendo as equações obtemos as coordenadas desejadas

Encontre as coordenadas do ponto médio do segmento  , cujos extremos são
, cujos extremos são  e
e  .
.
Encontre as coordenadas do ponto médio do segmento  , cujos extremos são
, cujos extremos são  e
e  .
.
1. As fórmulas para as coordenadas do ponto médio são:

2. Substituímos os valores de  e
e  nas duas fórmulas anteriores:
nas duas fórmulas anteriores:
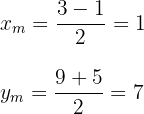
3. O ponto médio é 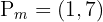 .
.
Encontre as coordenadas do ponto  , sabendo que
, sabendo que 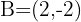 é o ponto médio de
é o ponto médio de  , onde
, onde 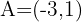 .
.
Encontre as coordenadas do ponto  , sabendo que
, sabendo que 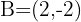 é o ponto médio de
é o ponto médio de  , onde
, onde 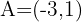 .
.
1. As fórmulas para as coordenadas do ponto médio são

2. Substituímos os valores de  e
e  nas duas fórmulas anteriores e calculamos a primeira coordenada de
nas duas fórmulas anteriores e calculamos a primeira coordenada de 
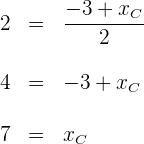
3. A segunda coordenada de  é
é
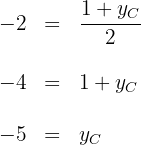
4. Por fim 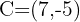
Descubra se os pontos  e
e  estão alinhados.
estão alinhados.
Descubra se os pontos  e
e  estão alinhados.
estão alinhados.
1. Os pontos 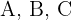 são colineares se as pendentes dos segmentos
são colineares se as pendentes dos segmentos  e
e  são iguais.
são iguais.

2. Como ambas pendentes são iguais, então os três pontos estão alinhados.
Calcule o valor de  para que os pontos
para que os pontos 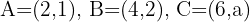 estejam alinhados.
estejam alinhados.
Calcule o valor de  para que os pontos
para que os pontos 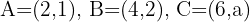 estejam alinhados.
estejam alinhados.
1. Os pontos 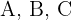 são colineares se as pendentes dos segmentos
são colineares se as pendentes dos segmentos  e
e  são iguais.
são iguais.
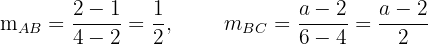
2. Como ambas pendentes são iguais, igualamos ambas expressões e isolamos 
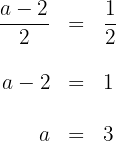
Dados os pontos 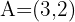 e
e 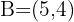 , encontre um ponto
, encontre um ponto  alinhado com
alinhado com  e
e  , de maneira que se obtenha
, de maneira que se obtenha  .
.
Dados os pontos 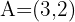 e
e 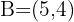 , encontre um ponto
, encontre um ponto 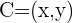 alinhado com
alinhado com  e
e  , de maneira que se obtenha
, de maneira que se obtenha  .
.
1. Partimos da condição dada e obtemos uma igualdade
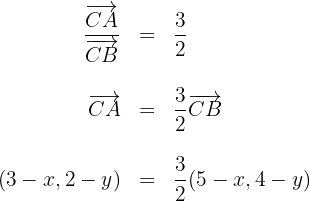
2. Igualamos ambas expressões, coordenada a coordenada, e obtemos
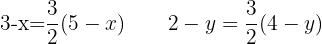
3. Resolvemos ambas equações para obter as coordenadas de 
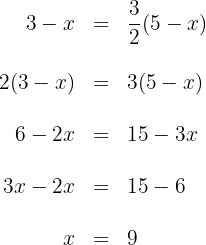
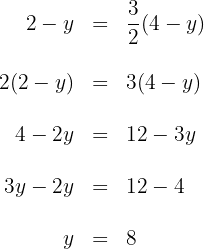
Dado um triângulo com vértices 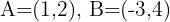 y
y  , encontre as coordenadas do baricentro.
, encontre as coordenadas do baricentro.
Dado um triângulo com vértices 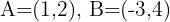 e
e  , encontre as coordenadas do baricentro.
, encontre as coordenadas do baricentro.
1. A fórmula para encontrar o baricentro é:

2. Substituindo os valores dos vértices do triângulo obtemos:

Dado um triângulo com dois de seus vértices 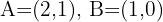 e baricentro
e baricentro 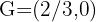 , calcule o terceiro vértice.
, calcule o terceiro vértice.
Dado um triângulo com dois de seus vértices 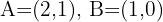 e baricentro
e baricentro 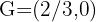 , calcule o terceiro vértice.
, calcule o terceiro vértice.
1. A fórmula para encontrar o baricentro é

2. Substituindo os valores do baricentro e os vértices do triângulo, obtemos duas equações

3. Resolvemos ambas equações e obtemos o terceiro vértice 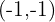 .
.
Encontre o simétrico do ponto 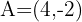 em relação a
em relação a 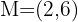 .
.
Encontre o simétrico do ponto 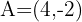 em relação a
em relação a 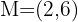 .
.
1. Expressamos 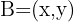 em relação ao simétrico de
em relação ao simétrico de  , que cumpre assim
, que cumpre assim 
2. Substituindo os valores dos pontos obtemos duas equações correspondentes às coordenadas dos vetores

3. Resolvemos ambas equações e obtemos  .
.
Encontre o simétrico do ponto  em relação a
em relação a 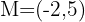 .
.
Encontre o simétrico do ponto  em relação a
em relação a 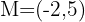 .
.
1. Expressamos 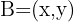 em relação ao simétrico de
em relação ao simétrico de  , que cumpre assim
, que cumpre assim 
2. Substituindo os valores dos pontos obtemos duas equações correspondentes às coordenadas dos vetores.

3. Resolvemos ambas equações e obtemos 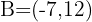 .
.
Quais os pontos de  e
e  dividem os segmentos de extremos
dividem os segmentos de extremos 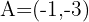 e
e 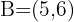 em três partes iguais?
em três partes iguais?
Quais os pontos de  e
e  dividem os segmentos de extremos
dividem os segmentos de extremos 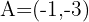 e
e 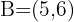 em três partes iguais?
em três partes iguais?
1. Em notação vetorial temos

2. Substituindo os valores dos pontos obtemos duas equações correspondentes às coordenadas dos vetores

3. Resolvemos ambas equações e obtemos 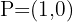 .
.
4. Para encontrar as coordenadas de  utilizamos a condição
utilizamos a condição
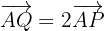
5. Substituindo os valores dos pontos obtemos duas equações correspondentes às coordenadas dos vetores

6. Resolvemos ambas equações e obtemos  .
.
Se o segmento  de extremos
de extremos 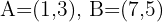 se dividem em quatro partes iguais, então quais são as coordenadas dos pontos de divisão?
se dividem em quatro partes iguais, então quais são as coordenadas dos pontos de divisão?
Se o segmento  de extremos
de extremos 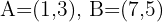 se dividem em quatro partes iguais, então quais são as coordenadas dos pontos de divisão?
se dividem em quatro partes iguais, então quais são as coordenadas dos pontos de divisão?
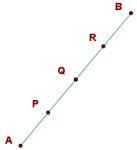
1. Notamos que  é o ponto médio do segmento
é o ponto médio do segmento 
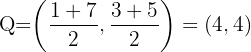
2.  é o ponto médio do segmento
é o ponto médio do segmento 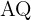

3.  é o ponto médio do segmento
é o ponto médio do segmento 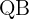
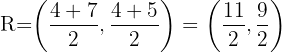
Resumir com IA:


