
Revisão da fórmula geral
Para resolver os exercícios utilizaremos a fórmula geral para equações de segundo grau:

Da qual utilizamos para resolver toda equação de segundo grau do tipo
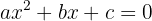 onde
onde 
Utilizar esse método é muito fácil já que apenas temos que igualar as equações a zero e substituir os valores de a,b,c na fórmula geral.
Ao resolver uma equação de segundo grau podem ocorrer 3 coisas:
- Existem 2 valores para a variável x que satisfaz a equação.
- Existe uma única solução.
- A solução não pertence ao conjunto dos números Reais.
Exercícios de equação quadráticas

1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos





3. A equação tem duas soluções reais diferentes


1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos





3. A equação tem duas soluções reais diferentes


1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos





3. A equação tem duas soluções reais diferentes

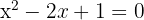
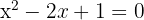
1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos


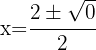


3. A equação tem apenas uma solução real


1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos




3. A equação não tem solução nos números reais.

1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos





3. A equação tem apenas uma solução real.



1. Passamos todos os termos para apenas um membro da equação para obter a seguinte forma 

2. Identificamos os valores de a, b e c

3. Substituímos na fórmula geral e resolvemos





4. A equação tem apenas uma solução real.



1. Resolvemos o binômio ao quadrado

2. Passamos todos os termos para um só lado e agrupamos para escrever a equação na seguinte forma 

3. Identificamos os valores de a, b e c

4. Substituímos na fórmula geral e resolvemos
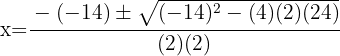




5. A equação tem duas soluções reais.


1. Neste caso podemos dividir ambos membros da equação por 7 para simplificá-la

2. Identificamos os valores de a, b e c

3. Substituímos na fórmula geral e resolvemos





4. A equação tem duas soluções reais.


1. Multiplicamos os dois membros por -1 para obtermos uma equação equivalente com a > 0


2. A equação não tem solução real

1. Utilizamos a propriedade distributiva para operar o parêntesis e obtermos:

2. Operamos e passamos tudo para o primeiro membro

3. Identificamos os valores de a, b e c

4. Substituímos na fórmula geral e resolvemos





5. A equação tem duas soluções reais.


1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos





3. A equação tem duas soluções reais diferentes
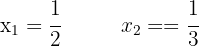

1. Resolvemos o binômio ao quadrado

2. Passamos todos os termos para um só lado e agrupamos para escrever a equação na seguinte forma 

3. Dividimos ambos membros da equação por 2 para simplificá-la

4. Identificamos os valores de a, b e c

5. Substituímos na fórmula geral e resolvemos





6. A equação tem duas soluções reais.


1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos





3. A equação tem duas soluções diferentes


1. Identificamos os valores de a, b e c

2. Substituímos na fórmula geral e resolvemos





3. A equação tem duas soluções reais diferentes


1. Multiplicamos o primeiro membro da equação por 6 e os últimos por 2 para eliminar o denominador 6, assim obtemos:

2. Identificamos os valores de a, b e c

3. Substituímos na fórmula geral e resolvemos





4. A equação tem duas soluções reais.

Resumir com IA:












