Um cilindro é um corpo geométrico gerado por um retângulo que gira ao redor de um de seus lados.
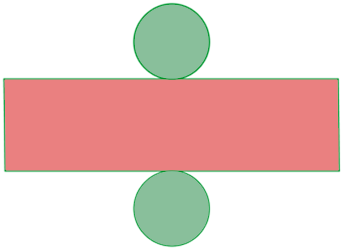
Elementos do cilindro
Um cilindro reto é formado de distintas partes que explicaremos a seguir
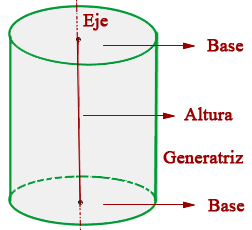
Bases do cilindro
São os círculos que conformam as bordas inferior e superior do cilindro. Estes círculos são iguais e paralelos.
Eixo do cilindro
É a reta que passa pelos centros das bases do cilindro; esta é perpendicular das bases. Observe que o eixo está ao lado do retângulo que gira sobre si mesmo.
Altura
É a longitude do segmento que tem como extremos os centros das duas bases. É igual ao lado do retângulo que gira sobre si mesmo.
Geratriz
É o lado oposto à altura e é o lado que gera o cilindro. Observe que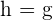 
Área lateral do cilindro
É igual à área da superfície do cilindro sem considerar a àrea de suas bases
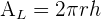
Área do cilindro
É igual à área total da superfície do cilindro considerando suas bases
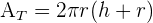
Volume do cilindro
Exercícios propostos
Calcule a quantidade de folhas metálicas que são necessárias para fazer 
latas de forma cilíndrica de 
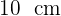de diâmetro e 
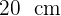de altura.
a) A quantidade de folha metálica necessária é a área total do cilindro
latex]{\begin{array}{rcl} A_T & = & 2\pi (5)(20 + 5) \\\\ & = & 785.4 \ cm^2 \end{array}}[/latex]
b) A quantidade total de folha metálica necessária para fabricar latas é
Um cilindro tem uma altura que é a mesma da longitude da circunferência da base. Se a altura é de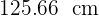 
. Calcule a área total e o volume.
a) Primeiro utilizamos o fato de que a altura é igual à longitude da circunferência da base para encontrarmos o valor do raio
b) Calculamos a área total
c) Calculamos o volume
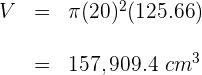
Em uma proveta de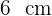 
de raio são colocados quatro cubos de gelo de 
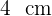de aresta. Em que altura vai chegar a água quando estiverem derretidos?
a) Calculamos o volume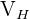 
de um cubo de gelo
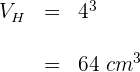
O volume ocupado pelos quatro cubos de gelo é 
b) Para encontrar a altura da proveta, igualamos o volume da proveta 
com o volume de água dos quatro cubos
Um recipiente cilíndrico de 10 cm de raio e 5 cm de altura está completamente cheio de água. Se a massa do recipiente cheio é de 2 kg, qual é a massa do recipiente vazio?
a) Calculamos o volume do recipiente
b) Sabemos que um 
é igual a um 
, dessa forma convertemos o volume para
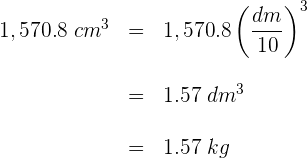
c) Assim, a massa do recipiente vazio é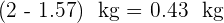 
Se o raio da base de um cilindro é reduzido à metade, seu volume é igual a metade do volume original?
a) Calculamos o volume do cilindro com raio 
e altura 
b) Calculamos o volume para o cilindro com o raio reduzido pela metade
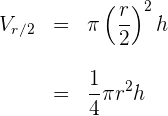
c) O volume do cilindro com o raio reduzido pela metade é igual à uma quarta parte do volume do cilindro original, e não a metade deste.
Queremos construir uma lata cilíndrica cujo raio seja a quarta parte de sua altura. Expresse o volume e a área total da lata em função do raio da mesma.
a) Calculamos o volume do cilindro com raio e altura
b) Utilizamos o fato de que o raio é igual a um quarto da altura para expressar a altura no termo do raio
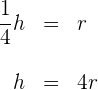
c) Substituímos o valor na fórmula do volume para expressar em termos de
d) Substituímos o valor na fórmula da área total para expressar em termos de
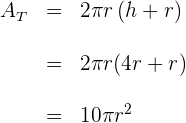
A altura de um cilindro é incrementada em 
unidades, qual é o incremento em seu volume?
a) Calculamos o volume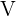 
do cilindro de raio e altura
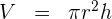
b) Calculamos o volume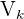 
do cilindro com o incremento de unidades na sua altura
O volume é incrementado em 
vezes a área de sua base
Qual é o volume de um cilindro com altura de 
que está em uma esfera com um raio de ?
a) Calculamos o raio do cilindro que está na esfera com um raio de , usando o teorema de Pitágoras
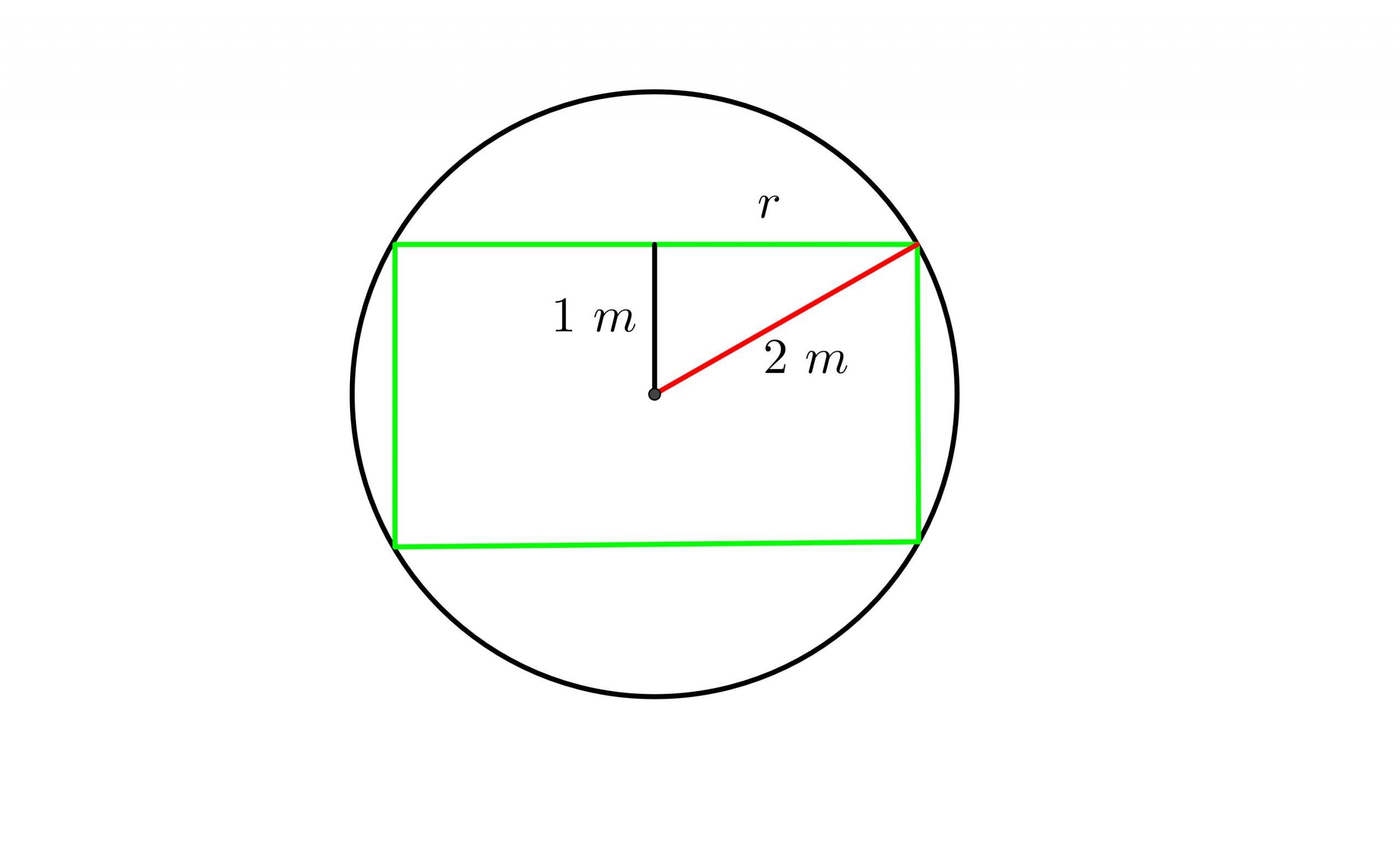
b) Calculamos o volume 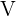do cilindro
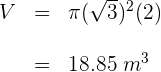
Construímos um cilindro de concreto com um diâmetro de 
, com espessura de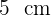 
e com uma altura de 
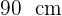. Qual é o volume de concreto necessário para construir o cilindro?
a) Calculamos o volume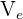 
do cilindro exterior com um diâmetro de e altura
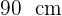
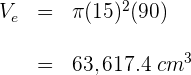
b) Calculamos o volume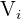 
do cilindro interior com um diâmetro de 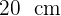e com uma altura de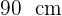
c) A quantidade 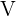de concreto utilizado é
.
Gostou desse artigo? Deixe uma nota!
Loading...
