Temas
- Razões trigonométricas em um triângulo retângulo
- Razões trigonométricas em uma circunferência
- Sinais das razões trigonométricas
- Tabela de razões trigonométricas
- Relações pitagóricas entre as razões trigonométricas
- Relações entre as razões trigonométricas de alguns ângulos
- Razões trigonométricas da soma e diferença de ângulos
- Razões trigonométricas do ângulo duplo
- Razões trigonométricas de meio ângulo
- Transformações de somas em produto
- Transformações de produtos em somas
- Exercícios de cálculo de seno, cosseno e tangente

Razões trigonométricas em um triângulo retângulo
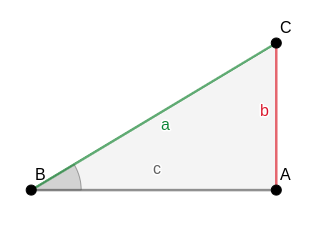
Seno
O seno do ângulo B é a razão entre o cateto oposto ao ângulo e a hipotenusa. É indicado por sen B.
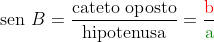
Cosseno
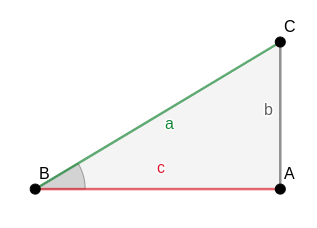
O cosseno do ângulo B é a razão entre o cateto adjacente ou contíguo ao ângulo e a hipotenusa. É indicado por cos B.
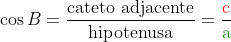
Tangente
A tangente do ângulo B é a razão entre o cateto oposto ao ângulo e o cateto adjacente ao ângulo. É indicado por tan B ou tg B.
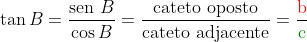
Cossecante
A cossecante do ângulo B é a razão inversa do seno de B.
Indicado por csc B ou cosec B.
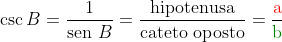
Secante
A secante do ângulo B é a razão inversa do cosseno de B.
É indicado por sec B.
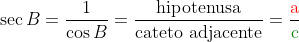
Cotangente
A cotangente do ângulo B é a razão inversa da tangente de B.
É indicado por cot B ou ctg B.
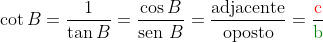
SOH-CAH-TOA: Uma maneira fácil de lembrar
SOH-CAH-TOA é um acrônimo usado para poder memorizar as definições das razões trigonométricas mais importantes: seno, cosseno e tangente.
Para as outras razões trigonométricas, em vez de criar outro acrônimo, é mais simples entender que a cossecante, secante e cotangente são opostos multiplicativos do seno, cosseno e tangente, respectivamente. Veja detalhadamente:

Razões trigonométricas em uma circunferência
Chamamos de círculo trigonométrico ou círculo unitário aquele que tem seu centro na origem de coordenadas e cujo raio é a unidade.
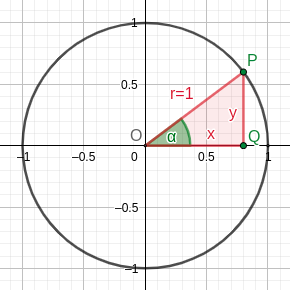
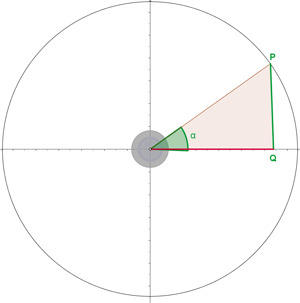
Como exemplo, um triângulo retângulo que está dentro do círculo com o raio formará a hipotenusa e se um dos catetos está sobre o eixo X, obteremos uma figura como a seguinte.
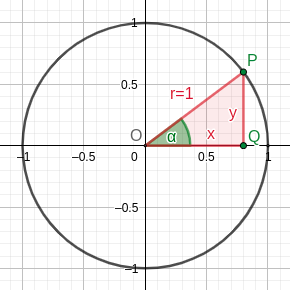
Calculamos o seno e cosseno do ângulo 
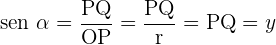
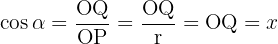
Concluímos que
O seno é a ordenada de P, isto é, do ponto que está sobre a circunferência.
O cosseno é a abscissa de P, isto é, do ponto que está sobre a circunferência.
Outro dado que podemos deduzir é que os valores de seno e cosseno estão entre 1 e -1.
-1 ≤ sen α ≤ 1
-1 ≤ cos α ≤ 1
Cabe destacar que a razão pela qual consideramos elas como funções trigonométricas no círculo é para podermos obter ângulos maiores. Por exemplo, de um triângulo retângulo não poderíamos saber quanto é 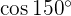 , porque não podemos construir um triângulo retângulo com um ângulo de 150°.
, porque não podemos construir um triângulo retângulo com um ângulo de 150°.
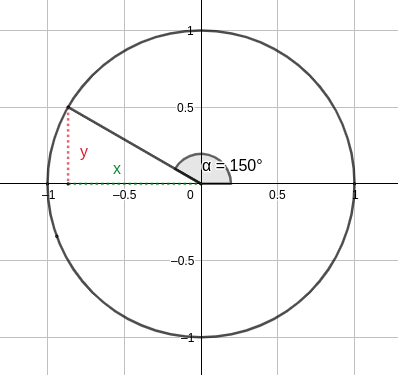
O círculo unitário nos permite fazer esse cálculo. O que devemos fazer é:
- Localizamos o ângulo de 150° que se forma a partir do eixo X na direção oposta aos ponteiros do relógio.
- Considero o ponto sobre a circunferência que se forma com o ângulo.
- A ordenada desse ponto é o seno
- A abscissa é o cosseno
Para as outras razões trigonométricas consideramos a seguinte figura
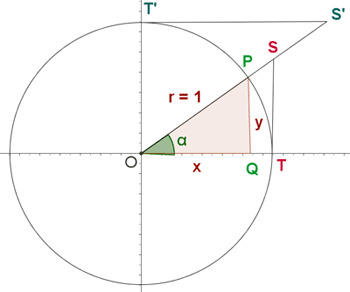
QOP e TOS são triângulos semelhantes. Então,

QOP e T'OS′ são triângulos semelhantes. Então,
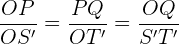
Usando as definições das razões trigonométricas e as relações entre os triângulos semelhantes, obtemos
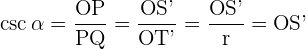
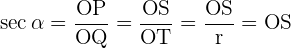

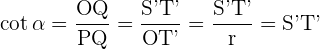
Sinais das razões trigonométricas
Na circunferência goniométrica os eixos de coordenadas delimitam quatro quadrantes que são numerados no sentido contrário aos ponteiros do relógio. Devemos lembrar que se consideramos um ângulo  e pegamos o triângulo retângulo dentro do círculo que é produzido com tal ângulo, o sinal de seno e cosseno deste ângulo vai depender em qual quadrante o triângulo está.
e pegamos o triângulo retângulo dentro do círculo que é produzido com tal ângulo, o sinal de seno e cosseno deste ângulo vai depender em qual quadrante o triângulo está.
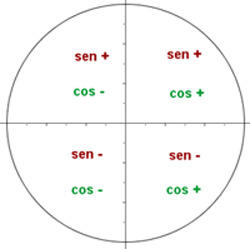
Tabela de razões trigonométricas

Relações pitagóricas entre as razões trigonométricas
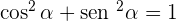
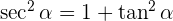

Explicação:
Como o triângulo dentro do círculo é retângulo, cumpre-se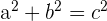
Na imagen, os catetos (a e b) correspondem aos valores x e y, e a hipotenusa ao raio, ou seja, 1.
Então 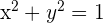
Como x é a abscissa y e a ordenada, sabemos que estes valores correspondem ao cosseno e seno respectivamente. Então,
Dividir a equação anterior por 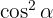 obtenho
obtenho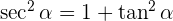
Se por outro lado tivesse dividido por  obteria
obteria
Relações entre as razões trigonométricas de alguns ângulos
Ângulos complementares
Dizemos que dois ângulos são complementares se sua soma é 90°, isto é, um ângulo reto.
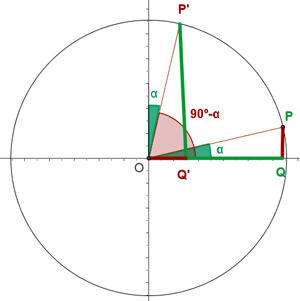


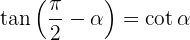
Ângulos suplementares
Dizemos que dois ângulos são suplementares se sua soma é 180°.
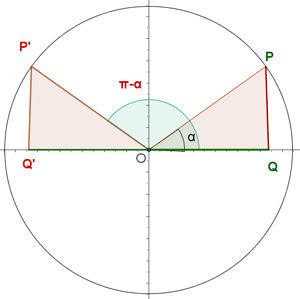

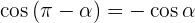

Ângulos que diferenciam em 180°
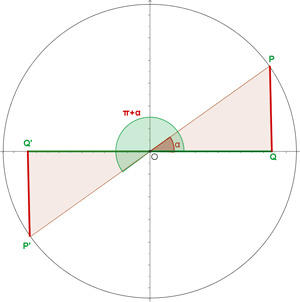

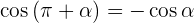
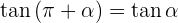
Ângulos opostos
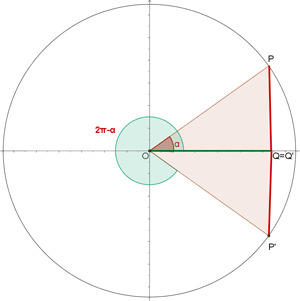


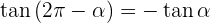
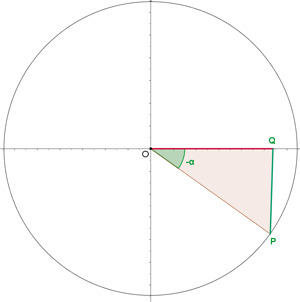
Ângulos negativos
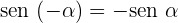

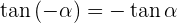
Maiores de 360º
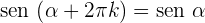
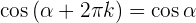
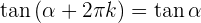
Ângulos que diferenciam em 90º
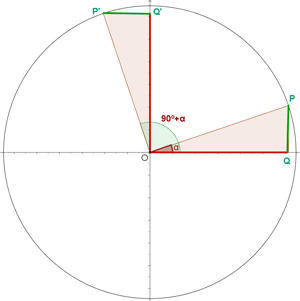
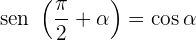
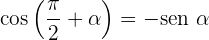
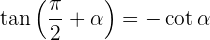
Ângulos que somam em 270º
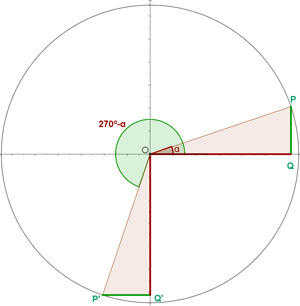
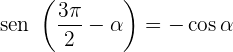
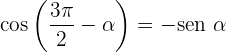
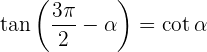
Ângulos que diferenciam em 270º
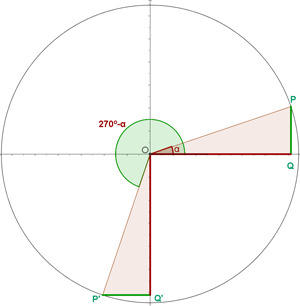
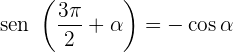

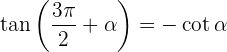
Razões trigonométricas da soma e diferença de ângulos
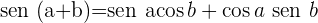
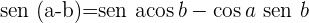


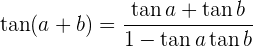

Razões trigonométricas do ângulo duplo

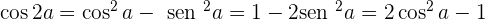
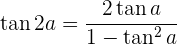
Razões trigonométricas de meio ângulo

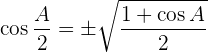
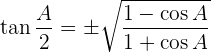
Transformações de somas em produto
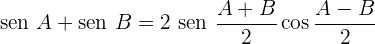
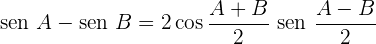
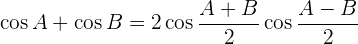
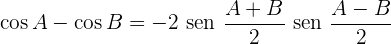
Transformações de produtos em somas
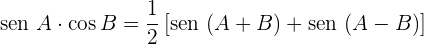


Exercícios de cálculo de seno, cosseno e tangente
Calcule seno, cosseno e tangente de  :
:
Seno: 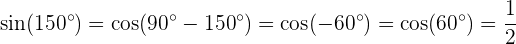
Cosseno: 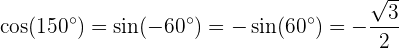
Tangente: 
Calcule seno, cosseno e tangente de 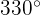 :
:
Seno: 
Cosseno: 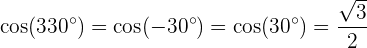
Tangente: 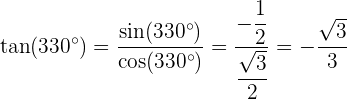
Resumir com IA:












