Temas
- Potências racionais
- Fatores em radicais
- Fatores fora do radical
- Igualando índices
- Soma de radicais
- Conversão de índices e soma de radicais
- Somas com radicais como denominadores
- Produto de radicais
- Divisões com radicais
- Simplifique a seguinte operação
- Hierarquia ao calcular radicais
- Potências de um radical
- Binômios e radicais
- Operações mistas com radicais
- Raízes de raízes
- Racionalização de radicais
- Leis de potências com radicais

Potências racionais
Calcule os valores das seguintes potências:
1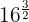
2
3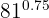
4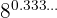
Calcule os valores das seguintes potências:
Solução:
Uma potência com expoente fracionário é igual a uma raiz cujo índice é o denominador da fração  e o expoente do radicando é o numerador
e o expoente do radicando é o numerador 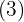 .
.
Para resolver o primeiro devemos antes decompor  em fatores, efetuamos as operações no radicando e extraímos os fatores
em fatores, efetuamos as operações no radicando e extraímos os fatores
1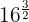
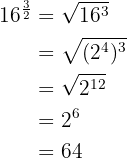
2
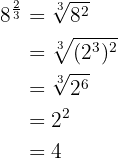
3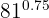
Neste caso, passamos o expoente que é um número decimal exato para fração
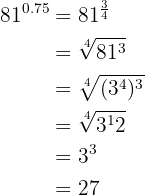
4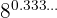
O expoente que é uma dízima periódica pura passaremos para fração
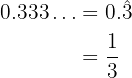
Uma vez que conhecemos o expoente como fração, resolvemos
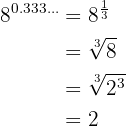
Fatores em radicais
Extraia os fatores:
1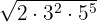
2
Extraia os fatores do radical:
Solução:
1 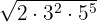
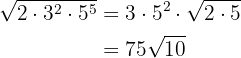
O expoente do dois  é menor que o índice
é menor que o índice  , portanto, está no radicando.
, portanto, está no radicando.
O expoente do 
 é igual ao índice
é igual ao índice  , portanto, o
, portanto, o  sai do radicando.
sai do radicando.
O expoente do 
 é maior que o índice
é maior que o índice  , portanto, dividimos este expoente pelo índice. O quociente obtido
, portanto, dividimos este expoente pelo índice. O quociente obtido  é o expoente do fator fora do radicando e o resto
é o expoente do fator fora do radicando e o resto  é o expoente do fator dentro do radicando.
é o expoente do fator dentro do radicando.
2 
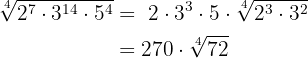
Os expoentes são maiores que o índice, portanto, dividimos esses expoentes pelo índice.
Cada um dos quocientes obtidos será o expoente do fator correspondente fora do radicando e cada um dos restantes será o expoente do fator correspondente dentro do radicando.

Fatores fora do radical
Introduza fatores:
1 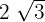
2
Introduza fatores:
Solução:
1 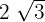
Antes de começarmos a resolver devemos lembrar algumas das propriedades dos radicais. Sabemos que o radical aplicado a um produto é o produto dos radicais
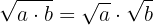
e que o índice do radical, quando passado para a forma exponencial, divide a potência da base

então, estes dois resultados juntos, utilizaremos para simplificar expressões com radicais multiplicados por fatores, isso é
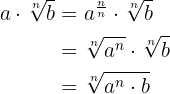
e, assim, podemos apenas utilizar o resultado

Aplicamos agora esse processo ao nosso problema:
Introduzimos o  elevado ao índice do radical
elevado ao índice do radical  e realizamos as operações
e realizamos as operações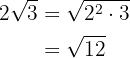
2
Introduzimos os fatores elevados ao índice 
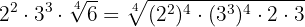
Fazemos as operações
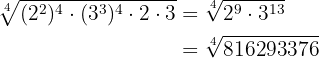
Igualando índices
Passe para índice comum:
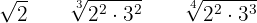
Passe para índice comum os radicais:
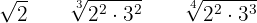
Solução:
Encontramos o mínimo múltiplo comum dos índices que será o índice comum

Dividimos o índice comum para cada um dos índices e cada resultado obtido multiplicamos pelos seus expoentes correspondentes
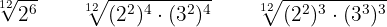
Fazemos as operações nos radicais
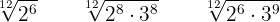
Soma de radicais
Faça as somas:
1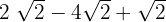
2
3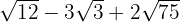
4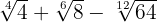
Faça as somas dos radicais:
Solução:
1 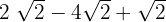
Como os radicais são semelhantes, somamos os coeficientes dos radicais:
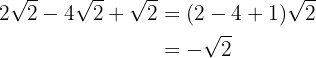
2 
Somamos os coeficientes dos radicais:
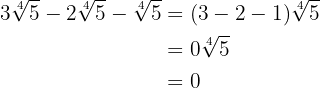
3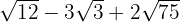
Decompomos em fatores os radicandos e extraímos os fatores dos radicais (se possível) e multiplicamos pelo coeficiente do radical correspondente
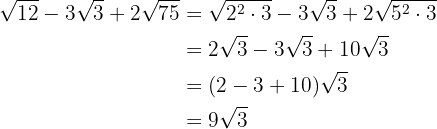
4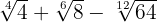
Extraímos os fatores dos radicais e multiplicamos pelo coeficiente do radical correspondente

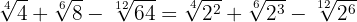
Simplificamos os radicais. No primeiro radical dividimos o índice e o expoente do radicando por  , no segundo por
, no segundo por  e no terceiro por
e no terceiro por 
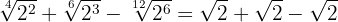
Somamos os coeficientes dos radicais
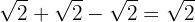
Conversão de índices e soma de radicais
Encontre as somas:
1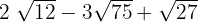
2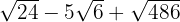
3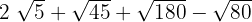
4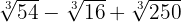
Encontre as somas dos radicais:
Solução:
Para fazer as somas de radicais não semelhantes, seguiremos o passo a passo:
Decompomos em fatores os radicais e extraímos os fatores dos radicais (se possível) e multiplicamos pelo coeficiente do radical correspondente
Somamos os coeficientes dos radicais
1 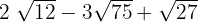
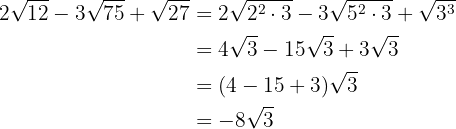
2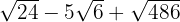
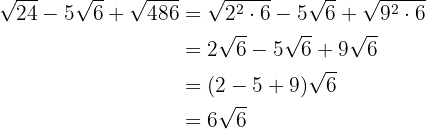
3 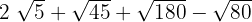
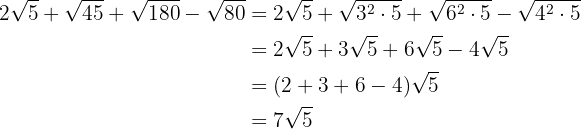
4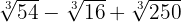
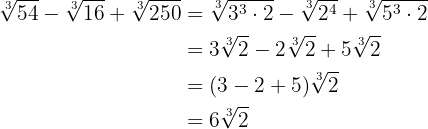
Somas com radicais como denominadores
Efetue as somas:
1
2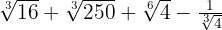
Efetue as somas dos radicais:
Solução:
1
Racionalizamos o segundo somando multiplicando e dividindo pela raiz quadrada de 
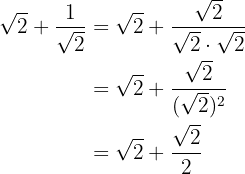
Tiramos o fator comum da raiz de  e somamos
e somamos
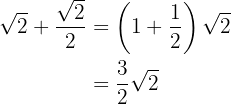
2 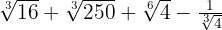
Decompomos em fatores os radicais

Nos dois primeiros, somamos extraindo os fatores, no terceiro, simplificamos o radical dividindo o índice e o expoente do radical entre  e, no último, vamos racionalizar multiplicando e dividindo pela raiz cúbica de
e, no último, vamos racionalizar multiplicando e dividindo pela raiz cúbica de 
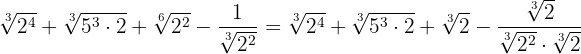
Como todos os radicais são semelhantes, podemos somar seus coeficientes
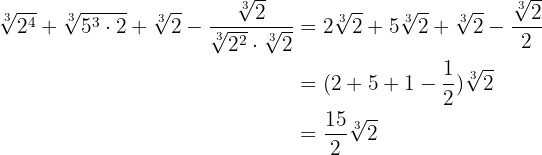
Produto de radicais
Calcule os produtos:
1
2
3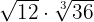
Calcule os produtos dos radicais:
Solução:
1 
Como os radicais têm o mesmo índice, multiplicamos os radicandos e decompomos em fatores para extrair os fatores do radical.
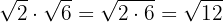
2 
Decompomos em fatores os radicandos
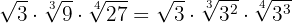
Reduzimos em índice comum, assim, temos que calcular o mínimo múltiplo comum dos índices, que será o índice comum.

Dividimos o índice comum  por cada um dos índices
por cada um dos índices  e cada resultado obtido multiplicaremos por seus expoentes correspondentes
e cada resultado obtido multiplicaremos por seus expoentes correspondentes  .
.
Calculamos o produto de potências com a mesma base no radicando e extraímos os fatores do radicando
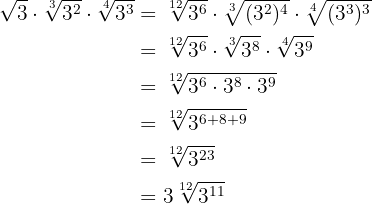
3 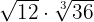
Calculamos o mínimo múltiplo comum dos índices.

Prosseguimos com os cálculos:
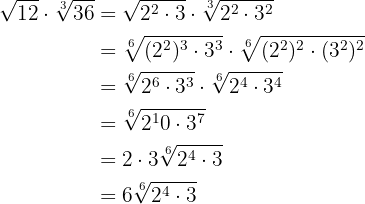
Divisões com radicais
Efetue as divisões com radicais:
1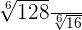
2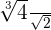
3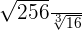
Efetue as divisões com radicais:
Solução:
1 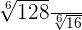
Como os radicais têm o mesmo índice, dividimos os radicandos e simplificamos o radical dividindo o índice e o expoente do radicando por 
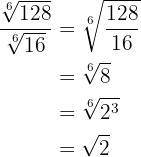
2 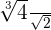
No primeiro reduzimos em índice comum, assim, temos que calcular o mínimo múltiplo comum dos índices, que será o índice comum.
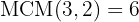 .
.
Dividimos o índice comum  por cada um dos índices
por cada um dos índices 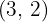 e cada resultado obtido multiplicaremos por seus expoentes correspondentes
e cada resultado obtido multiplicaremos por seus expoentes correspondentes 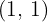 .
.
Decompomos o  em fatores para poder fazer a divisão de potências com a mesma base e dividimos.
em fatores para poder fazer a divisão de potências com a mesma base e dividimos.
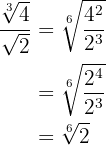
3 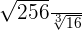
Fazemos os mesmos passos do exercício anterior
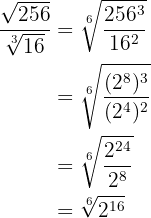
Simplificamos o radical dividindo por  o índice e o expoente do radicando. Por último, extraímos os fatores
o índice e o expoente do radicando. Por último, extraímos os fatores
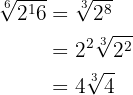
Simplifique a seguinte operação
Calcule:

Calcule:

Primeiro, calculamos o mínimo múltiplo comum dos índices, que será o índice comum
Dividimos o índice comum  por cada um dos índices
por cada um dos índices 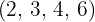 e cada resultado obtido multiplicaremos por seus expoentes correspondentes
e cada resultado obtido multiplicaremos por seus expoentes correspondentes 
Removemos os parênteses, simplificamos a fração e multiplicamos no numerador as potências com mesma base.
Simplificamos o radical dividindo por  o índice e o expoente do radicando.
o índice e o expoente do radicando.
Por último, extraímos os fatores:

Hierarquia ao calcular radicais
Faça a operação:
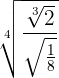
Faça a operação:
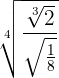
Solução:
Primeiro, devemos notar que 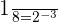 , portanto
, portanto
Passamos para índice comum as raízes do numerador e do denominador.
Elevamos ao cubo o denominador e realizamos a divisão de potências com mesma base.
Calculamos a raiz quarta do radical multiplicando os índices.
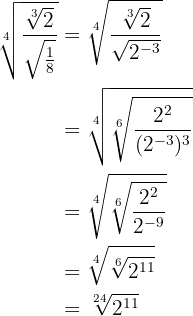
Potências de um radical
Faça as operações com potências:
1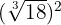
2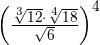
Faça as operações com potências:
Solução:
1 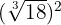
Elevamos o radicando ao quadrado, decompomos  em fatores e elevamos ao quadrado e, por último, extraímos os fatores
em fatores e elevamos ao quadrado e, por último, extraímos os fatores
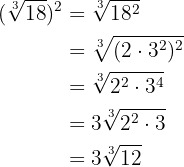
2 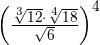
Elevamos os radicandos à quarta, decompomos os radicandos em fatores e extraímos o  do radical
do radical
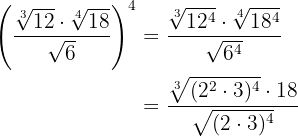
Fazemos as operações com potências nos radicandos e, depois, passamos para índice comum para poder efetuar a divisão
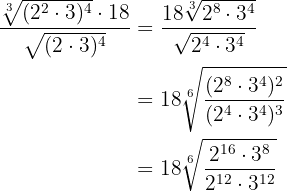
Simplificamos o radical dividindo por  o índice e os expoentes do radicando, depois fazemos uma divisão de potências com o mesmo expoente
o índice e os expoentes do radicando, depois fazemos uma divisão de potências com o mesmo expoente
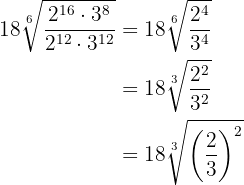
Podemos racionalizar multiplicando e dividindo pela raiz cúbica de 
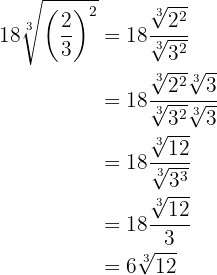
Binômios e radicais
Faça as operações:
1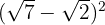
2
3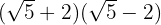
4
Faça as operações:
Solução:
1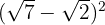
Um quadrado da diferença é igual ao quadrado do primeiro termo, menos o dobro do primeiro pelo segundo, mais o quadrado do segundo
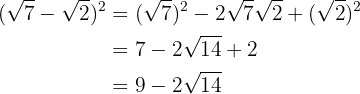
2
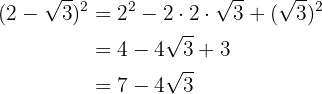
3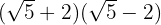
Uma soma pela diferença é igual à diferença de quadrados
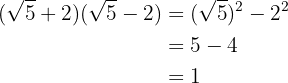
4
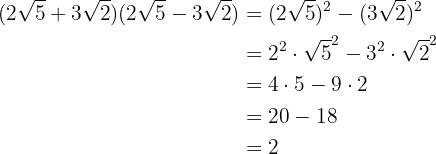
Operações mistas com radicais
Calcule:
1
2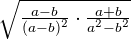
Calcule:
Solução:
1
Fazemos a multiplicação de frações. No denominador temos uma soma pela diferença que é igual à diferença de quadrados
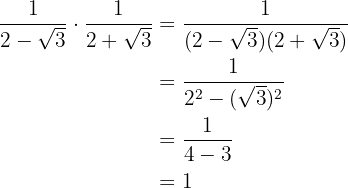
2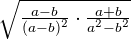
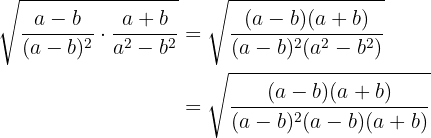
A diferença de quadrados do denominador colocamos como uma soma pela diferença e simplificamos a fração
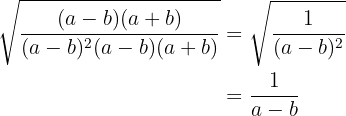
Raízes de raízes
Efetue:
1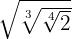
2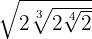
3
Efetue:
Solução:
1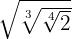
Multiplicando os índices
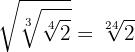
2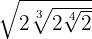
Introduzimos o primeiro termo  dentro da raiz cúbica, dessa maneira, teremos que elevá-lo ao cubo e depois multiplicamos as potências com mesma base. Continuamos fazendo o procedimento até que todos os valores tenham sido introduzidos nos radicais. Assim, multiplicamos
dentro da raiz cúbica, dessa maneira, teremos que elevá-lo ao cubo e depois multiplicamos as potências com mesma base. Continuamos fazendo o procedimento até que todos os valores tenham sido introduzidos nos radicais. Assim, multiplicamos  e então temos
e então temos 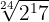 .
.
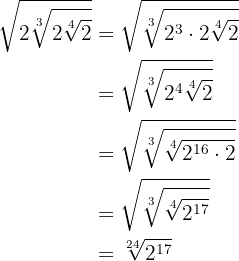
3
Introduzimos o  dentro da raiz quadrada elevando-o ao quadrado.
dentro da raiz quadrada elevando-o ao quadrado.
Multiplicamos as potências com mesma base.
Multiplicamos os índices e simplificamos dividindo por 3 o índice resultante e o expoente do radicando.
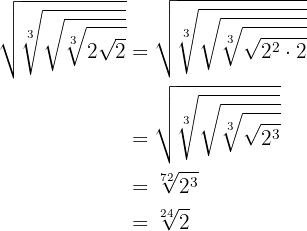
Racionalização de radicais
Racionalize os radicais:
1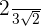
2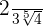
3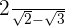
4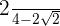
5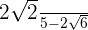
Racionalize os radicais:
Solução:
1 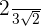
Multiplicamos o numerador e denominador pela raiz de  . Fazemos os cálculos e simplificamos a fração.
. Fazemos os cálculos e simplificamos a fração.
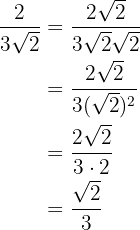
2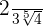
O radicando  vamos transformar em forma de potência:
vamos transformar em forma de potência:  .
.
Temos que multiplicar o numerador e denominador pela raiz quinta de  .
.
Multiplicamos os radicais do denominador, extraímos os fatores do radical e simplificamos a fração.
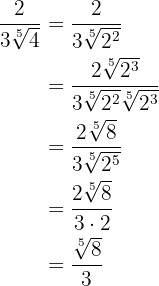
3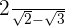
Multiplicamos o numerador e denominador pelo conjugado do denominador, removemos os parênteses do numerador e efetuamos a soma pela diferença no denominador. Assim, obtemos uma diferença de quadrados.
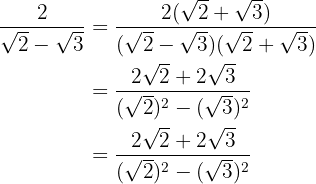
Extraímos os radicandos do denominador e dividimos por  . Ou seja, mudamos o sinal do numerador.
. Ou seja, mudamos o sinal do numerador.
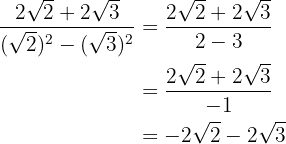
4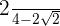
Multiplicamos e dividimos a fração pelo conjugado do denominador.
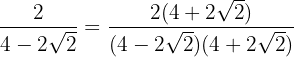
Efetuamos a soma pela diferença no denominador. Dessa forma, obtemos uma diferença de quadrados, depois calculamos:
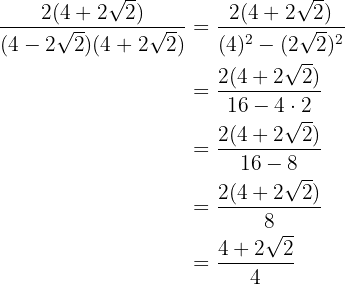
5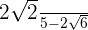
Multiplicamos o numerador e denominador pelo conjugado do denominador removemos os parênteses do numerador e efetuamos a soma pela diferença no denominador. Assim, obtemos uma diferença de quadrados.
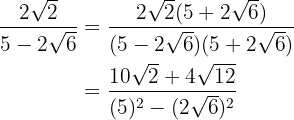
Decompomos em fatores o numerador  e extraímos os fatores. Terminamos fazendo as operações do denominador.
e extraímos os fatores. Terminamos fazendo as operações do denominador.
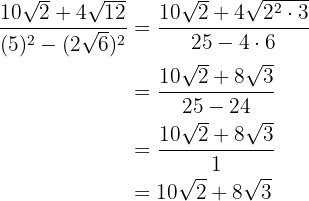
Leis de potências com radicais
Racionalize:
1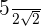
2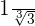
3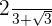
4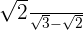
5
Racionalize:
Solução:
1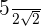
Multiplicamos o numerador e denominador pela raiz de  e fazemos os cálculos
e fazemos os cálculos
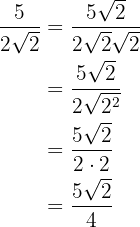
2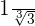
Aqui nos damos conta de que para poder eliminar o radical de  precisamos gerar o produto
precisamos gerar o produto
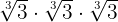
para que desta forma o radical seja eliminado, ou seja
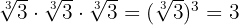
em outras palavras, como já temos  no denominador, precisamos apenas multiplicá-lo por
no denominador, precisamos apenas multiplicá-lo por  para conseguir eliminar o radical.
para conseguir eliminar o radical.
Para não afetar o valor numérico da expressão, multiplicamos  tanto no numerador como no denominador. Então, nosso cálculo fica assim
tanto no numerador como no denominador. Então, nosso cálculo fica assim
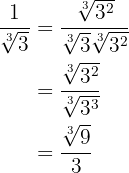
3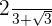
Multiplicamos e dividimos a fração pelo conjugado do denominador.
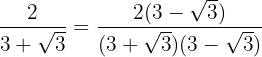
Removemos os parênteses do numerador e efetuamos a soma pela diferença no denominador. Assim, obtemos uma diferença de quadrados.
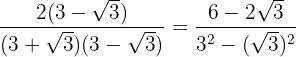
Efetuamos as operações e simplificamos a fração fatorando o 
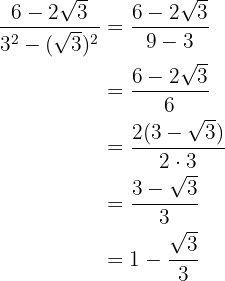
4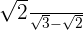
Multiplicamos e dividimos a fração pelo conjugado do denominador
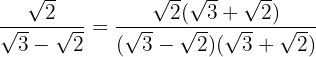
Removemos os parênteses do numerador e efetuamos a soma pela diferença no denominador. Assim, obtemos uma diferença de quadrados
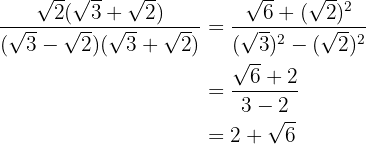
5
Multiplicamos o numerador e denominador pelo conjugado do denominador

Transformamos o numerador em forma de potência

Temos uma diferença ao quadrado no numerador que é igual ao quadrado do primeiro termo, menos o dobro do primeiro pelo segundo, mais o quadrado do segundo. Temos uma soma pela diferença no denominador que é igual à diferença de quadrados

Fazemos as operações e simplificamos no final
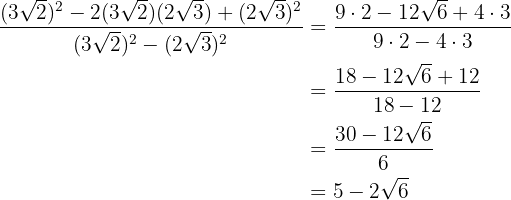
Resumir com IA:












