Porcentagem – Enem 2021 (Adaptado)
Para realizar um voo entre duas cidades que distam  km uma da outra, uma companhia aérea utilizava um modelo de aeronave A, capaz de transportar até
km uma da outra, uma companhia aérea utilizava um modelo de aeronave A, capaz de transportar até  passageiros. Quando uma dessas aeronaves está lotada de passageiros, o consumo de combustível é de
passageiros. Quando uma dessas aeronaves está lotada de passageiros, o consumo de combustível é de 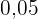 litro por quilômetro e por passageiro. Essa companhia resolveu trocar o modelo de aeronave A pelo modelo de aeronave B, que é capaz de transportar 50% de passageiros a mais do que o modelo A, mas consumindo
litro por quilômetro e por passageiro. Essa companhia resolveu trocar o modelo de aeronave A pelo modelo de aeronave B, que é capaz de transportar 50% de passageiros a mais do que o modelo A, mas consumindo  % menos combustível por quilômetro e por passageiro. Calcule a quantidade de combustível consumida pelo modelo de aeronave B, em relação à do modelo de aeronave A, em um voo lotado entre as duas cidades.
% menos combustível por quilômetro e por passageiro. Calcule a quantidade de combustível consumida pelo modelo de aeronave B, em relação à do modelo de aeronave A, em um voo lotado entre as duas cidades.
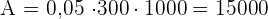 Litros
Litros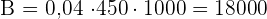 Litros
Litros
Calcular total gasto em cada companhia e aplicar a Fórmula da Variação percentual:
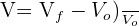
Onde: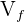 =Valor final
=Valor final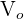 =Valor inicial
=Valor inicial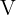 =Variação percentual
=Variação percentual
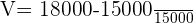
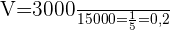
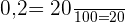
Análise Combinatória – Enem 2021 (Adaptado)
Uma pessoa produzirá uma fantasia utilizando como materiais:  tipos de tecidos diferentes e
tipos de tecidos diferentes e  tipos distintos de pedras ornamentais. Essa pessoa tem à sua disposição
tipos distintos de pedras ornamentais. Essa pessoa tem à sua disposição  tecidos diferentes e
tecidos diferentes e  pedras ornamentais distintas. A quantidade de fantasias com materiais diferentes que podem ser produzidas é representada pela expressão:
pedras ornamentais distintas. A quantidade de fantasias com materiais diferentes que podem ser produzidas é representada pela expressão:
A. 
B. 
C. 
Aplicar fórmula da Combinação (ordem das escolhas não altera o resultado):

Onde: = número total de elementos
= número total de elementos = número total de posições
= número total de posições
Aplicar para os tecidos (escolha de  em
em  tipos diferentes):
tipos diferentes):
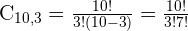
Aplicar para as pedras (escolha de  em
em  tipos diferentes):
tipos diferentes):
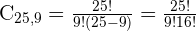
Multiplicar ambos, pois o enunciado utiliza o conectivo “e”.
Sólidos Geométricos – Enem 2021 (Adaptado)
Um povoado com  habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 6 metros de diâmetro interno, e atender à demanda de água da população por um período de 1 mês consecutivo. Considere que o consumo médio diário por habitante é de
habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 6 metros de diâmetro interno, e atender à demanda de água da população por um período de 1 mês consecutivo. Considere que o consumo médio diário por habitante é de  litros de água. Use
litros de água. Use  como aproximação para
como aproximação para  . Nas condições apresentadas, o reservatório deverá ser construído com uma altura interna mínima, em metro, igual a:
. Nas condições apresentadas, o reservatório deverá ser construído com uma altura interna mínima, em metro, igual a:
A.  metros
metros
B.  metros
metros
C.  metros
metros
Calcular o consumo total de água dos habitantes em 1 mês:
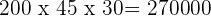 litros
litros
Aplicar fórmula do Volume do Cilindro:
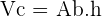
Onde
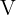 = Volume
= Volume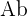 = Área da base
= Área da base = Altura
= Altura
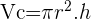
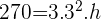
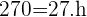
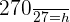
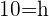
Razão e Proporção – Enem 2020 (Adaptado)
Um pé de eucalipto em idade adequada para o corte rende, em média,  mil folhas de um determinado tipo de papel. A densidade superficial do papel, medida pela razão da massa de uma folha desse papel por sua área, é de
mil folhas de um determinado tipo de papel. A densidade superficial do papel, medida pela razão da massa de uma folha desse papel por sua área, é de  gramas por metro quadrado, e a área de uma folha desse papel é
gramas por metro quadrado, e a área de uma folha desse papel é 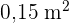 . Nessas condições, quantos quilogramas de papel rende, em média, um pé de eucalipto?
. Nessas condições, quantos quilogramas de papel rende, em média, um pé de eucalipto?
Aplicar a razão da massa pela área, para descobrir a densidade superficial do papel:
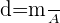
Onde:
 densidade
densidade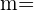 massa
massa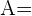 área
área
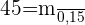
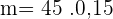
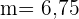 g
g
 eucalipto possui capacidade de
eucalipto possui capacidade de  folhas de papel. Logo temos:
folhas de papel. Logo temos:
 papel
papel
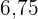 g
g papéis
papéis
 g
g

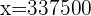 g ou
g ou  Kg
Kg
Escala – Enem 2020 (Adaptado)
A caixa-d’água de um edifício terá a forma de um paralelepípedo retângulo reto com volume igual a 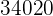 litros. Em uma maquete que representa o edifício, a caixa-d’água tem dimensões
litros. Em uma maquete que representa o edifício, a caixa-d’água tem dimensões  cm x
cm x 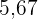 cm x
cm x  cm.
cm.
Dado: 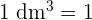 L.
L.
A escala usada pelo arquiteto foi:
A. 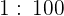
B. 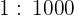
C. 
Aplicar Fórmula da Escala Volumétrica:
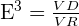
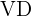 = volume do desenho
= volume do desenho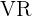 = volume real
= volume real
Calculando o Volume do Desenho:
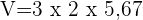
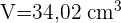
Passando para 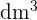
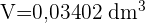
Como 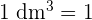 Litro
Litro
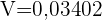 Litros
Litros
Substituindo na fórmula para achar a escala:
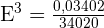
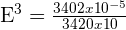
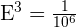
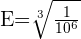
 ou
ou 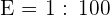
Razão e Proporção – Enem 2020 (Adaptado)
Uma torneira está gotejando água em um balde com capacidade de  litros. No instante atual, o balde se encontra com ocupação de
litros. No instante atual, o balde se encontra com ocupação de  % de sua capacidade. A cada segundo caem
% de sua capacidade. A cada segundo caem  gotas de água da torneira, e uma gota é formada, em média, por
gotas de água da torneira, e uma gota é formada, em média, por  x
x 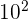 mL de água. Quanto tempo, em hora, será necessário para encher completamente o balde, partindo do instante atual?
mL de água. Quanto tempo, em hora, será necessário para encher completamente o balde, partindo do instante atual?
Utilizar  regras de
regras de  simples e diretamente proporcionais:
simples e diretamente proporcionais:
I) Primeiro achar quanto de água é equivalente a  % do balde (parte que será enchida):
% do balde (parte que será enchida):
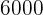 mL
mL 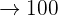
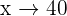 %
%
II) Descobrir quantos segundos demorará para encher o balde:
 segundo
segundo 
 segundos
segundos 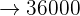 mL
mL
 segundos
segundos
III) Depois, transformar o tempo em horas:
 minutos
minutos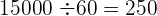 horas
horas
Média Aritmética – Enem 2020 (Adaptado)
O preparador físico de um time de basquete dispõe de um plantel de  jogadores, com média de altura igual a
jogadores, com média de altura igual a 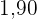 m. No último treino antes da estreia em um campeonato, um dos jogadores desfalcou o time em razão de uma séria contusão, forçando o técnico a contratar outro jogador para recompor o grupo. Se o novo jogador é
m. No último treino antes da estreia em um campeonato, um dos jogadores desfalcou o time em razão de uma séria contusão, forçando o técnico a contratar outro jogador para recompor o grupo. Se o novo jogador é 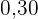 m mais alto que o anterior, qual é a média de altura, em metro, do novo grupo?
m mais alto que o anterior, qual é a média de altura, em metro, do novo grupo?
Aplicando fórmula da média aritmética:
Média 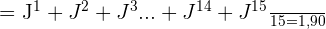
Vamos supor que o jogador substituído foi o 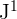 , logo:
, logo:
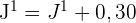
Então a fórmula da média ficará:
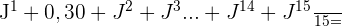 Nova Média
Nova Média
Podemos reescrevê-la separando os termos:
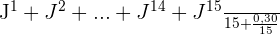
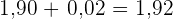 metros
metros
Porcentagem – Enem 2021 (Adaptado)
Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), o rendimento médio mensal dos trabalhadores brasileiros, no ano 2000, era de R$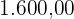 . Já o Censo 2010 mostrou que, em 2010, esse valor teve um aumento de
. Já o Censo 2010 mostrou que, em 2010, esse valor teve um aumento de  % em relação a 2000. Esse mesmo instituto projeta que, em 2020, o rendimento médio mensal dos trabalhadores brasileiros poderá ser
% em relação a 2000. Esse mesmo instituto projeta que, em 2020, o rendimento médio mensal dos trabalhadores brasileiros poderá ser  % maior do que foi em 2010. Supondo que as projeções do IBGE se realizem, o rendimento médio mensal dos brasileiros em 2020 será de:
% maior do que foi em 2010. Supondo que as projeções do IBGE se realizem, o rendimento médio mensal dos brasileiros em 2020 será de:
A. R$ 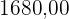
B. R$ 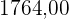
C. R$ 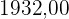
Utilizar Fórmula do aumento percentual:
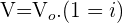
Onde: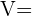 valor final
valor final valor inicial
valor inicial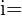 aumento percentual
aumento percentual
Ano de 2010:
Aumento percentual de 5% em relação a 2000 (R$ 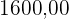 ):
):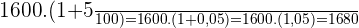
Ano de 2020:
Aumento percentual de 15 % em relação a 2010 (R$ 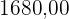 ):
):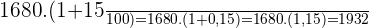
Álgebra – Enem 2018 (Adaptado)
Uma loja vende automóveis em  parcelas iguais sem juros. No momento de contratar o financiamento, caso o cliente queira aumentar o prazo, acrescentando mais
parcelas iguais sem juros. No momento de contratar o financiamento, caso o cliente queira aumentar o prazo, acrescentando mais  parcelas, o valor de cada uma das parcelas diminui R$
parcelas, o valor de cada uma das parcelas diminui R$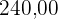 , ou se ele quiser diminuir o prazo, com 3 parcelas a menos, o valor de cada uma das parcelas sobe R$
, ou se ele quiser diminuir o prazo, com 3 parcelas a menos, o valor de cada uma das parcelas sobe R$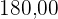 . Considere ainda que, nas três possibilidades de pagamento, o valor do automóvel é o mesmo, todas são sem juros e não é dado desconto em nenhuma das situações. Nessas condições, qual é a quantidade N de parcelas a serem pagas de acordo com a proposta inicial da loja?
. Considere ainda que, nas três possibilidades de pagamento, o valor do automóvel é o mesmo, todas são sem juros e não é dado desconto em nenhuma das situações. Nessas condições, qual é a quantidade N de parcelas a serem pagas de acordo com a proposta inicial da loja?
Segundo o enunciado temos  equações:
equações:
I) 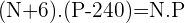
II) 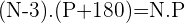
Equação I)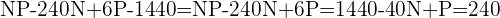
Equação II)
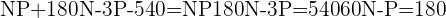
Resolvendo as  equações, por adição, para achar
equações, por adição, para achar  :
:
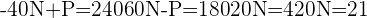
Prismas - Enem 2017 (Adaptado)
Uma empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugerem que seja adicionado 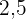 mL desse produto para cada
mL desse produto para cada  L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a
L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 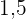 m, com largura e comprimento iguais a
m, com largura e comprimento iguais a  m e
m e  m, respectivamente. O nível da lâmina d'água dessa piscina é mantido a
m, respectivamente. O nível da lâmina d'água dessa piscina é mantido a  cm da borda da piscina.
cm da borda da piscina.
A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é:
A.  mL
mL
B.  mL
mL
C.  mL
mL
Converter todas as medidas para  , pois
, pois 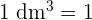 L
L
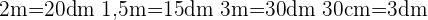
Calcular Volume total da piscina cheia de água:
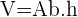
Onde: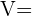 Volume
Volume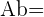 Área da base
Área da base =Altura
=Altura
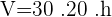
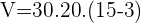
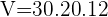
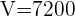 litros
litros
Achar  para descobrir quantos mL de produto foram utilizados:
para descobrir quantos mL de produto foram utilizados:
Regra de  diretamente proporcional:
diretamente proporcional:
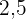 mL
mL 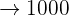 Litros
Litros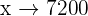 Litros
Litros
 mL
mL
Resumir com IA:



