As propriedades dos determinantes

1 O determinante de uma matriz e o determinante de sua transposta 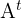são iguais.

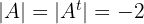
2     Se:

Possui duas linhas (ou colunas) iguais:

Todos os elementos de uma linha (ou coluna) são nulos:

Os elementos de uma linha (ou coluna) são combinação linear das outras:

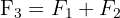
3  O determinante de uma matriz triangular é igual ao produto dos elementos da diagonal principal.

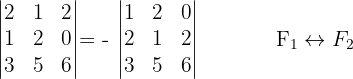
4  Se em um determinante trocamos entre si duas linhas (ou duas colunas), seu valor muda apenas de sinal.

5  Se a elementos de uma linha (ou coluna) somamos os elementos de outra multiplicados previamente por um número real, o valor do determinante não varia. Ou seja, se transformarmos uma linha (ou coluna) em uma combinação linear das outras, o valor do determinante não muda.

6  Se multiplicamos um determinante por um número real, o valor do determinante será multiplicado por esse número apenas em uma linha (ou coluna).

7  Se todos os elementos de uma linha (ou coluna) forem compostos por dois somatórios, o determinante pode ser decomposto na soma de dois determinantes, nos quais as outras linhas (ou colunas) permanecem inalteradas.

8 

O determinante de um produto é igual ao produto dos determinantes.