Se você tem um problema com um modelo que possui condições de contorno definidas, mas também deseja que esse modelo tenha certa flexibilidade para ser resolvido mais facilmente por diferentes métodos, é importante saber o que é um produto escalar.
Pode ser que nem sempre você compreenda o que é um produto escalar, já que a definição costuma envolver equações matemáticas mais complexas, mas isso não diminui sua importância para o entendimento de outros conceitos da física. Em particular, quando estudamos condições de contorno na atmosfera, como nuvens de baixa altitude ou pancadas de chuva, a inclusão de um produto escalar na formulação facilita a resolução do problema.
Um produto escalar é uma quantidade escalar ou vetorial que possui um valor definido positivo, mas que não é necessariamente zero. Em outras palavras, ele representa uma variação de alguma quantidade mensurável, como um vetor, e não necessariamente a posição ou direção real para a qual o vetor aponta. Os produtos escalares de dois ou mais vetores costumam ser definidos como a soma de todas as quantidades vetoriais correspondentes, embora isso não seja obrigatório.
O produto escalar de dois vetores é uma operação que recebe dois vetores e produz um número real:
Observe que o produto escalar normalmente é indicado por um ponto, como em . Outra notação usada é . No entanto, neste material usaremos sempre o ponto.
Além disso, o produto escalar não deve ser confundido com a multiplicação de um vetor por um escalar.
Formas de calcular o produto escalar
Existem duas maneiras equivalentes de obter o produto escalar de dois vetores 
e 
. São elas:
1 Se conhecemos o módulo dos dois vetores e o ângulo
que formam entre eles, então o produto escalar é dado por
2 Se conhecemos os componentes dos vetores 
e 
, então o produto escalar é dado por
Exemplos
1 Considerando os vetores e . Além disso, o ângulo entre eles é .
Para calcular o produto escalar, primeiro encontramos o módulo de e :
Assim, o produto escalar é:
2 Repetindo o exemplo anterior: e . Mas, agora, utilizamos uma outra fórmula:
Observe que o resultado foi o mesmo.
Cálculo do módulo e do ângulo entre vetores
Como vimos, existem duas fórmulas equivalentes para o produto escalar. Assim, podemos usar o produto escalar para calcular o módulo de um vetor ou o ângulo entre dois vetores.
Calcular o módulo usando o produto escalar
Se é um vetor, então:
Portanto,
Esta fórmula é utilizada para calcular o módulo de um vetor utilizando o producto escalar de .
Calcular o ângulo entre vetores usando o produto escalar
Suponha que temos os vetores e . Então:
Isolando , temos:
Substituindo a outra fórmula de produto escalar:
Esta fórmula é utilizada para calcular a função arcocosseno.
Exemplos
1 Considerando os vetores e . ntão, o módulo desses vetores é:
2 Agora calcularemos o ângulo entre e . Temos que:
De maneira que:
Portanto,
Ortogonalidade de dois vetores
Sabemos que dois vetores são ortogonais (ou perpendiculares) se o ângulo entre eles é ou . Em qualquer desses casos, temos 
. Portanto, se dois vetores são ortogonais, então:
Ou seja, dois vetores e serão ortogonais sempre que:
Exemplo
Verificaremos a ortogonalidade dos vetores e usados nos exemplos anteriores. Observamos que:
Portanto, os vetores e não são perpendiculares.
Interpretação geométrica do produto escalar
Notamos que pode ser visto como o módulo da projeção do vetor sobre , sempre que 
como mostra a figura. A projeção seria o vetor com origem em
e extremidade em 
.
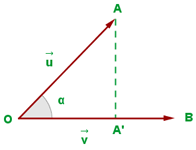
Isso parte da observação do triângulo retângulo formado na figura. Sabemos que:
De maneira que, ao isolar 
, temos:
Para imaginar a projeção, pense em uma fonte de luz: a projeção é a “sombra” do vetor sobre o vetor . Além disso, essa fonte de luz deve estar colocada de tal forma que um vetor perpendicular a não projete sombra alguma.
Deste modo, o produto 
pode ser visto como o módulo de um dos vetores multiplicado pelo módulo da projeção do outro. Substituindo 
na fórmula do produto escalar, temos:
Portanto, podemos calcular o módulo da projeção de sobre o vetor utilizando
Observação: Se for negativo,isso indica que a projeção tem sentido contrário ao vetor . Isso que ocorre quando 
ou 
. Nesse caso, o módulo da projeção é 
.
Exemplo
Vamos encontrar a projeção de 
sobre el vetor 
. Para isso, calculamos:
Observe que tem sinal negativo.Logo, a projeção tem sentido contrário ao de e seu módulo é .
Propriedades do produto escalar
O produto escalar satisfaz diversas propriedades. As principais são:
1 Comutatividade: a ordem dos fatores não altera o resultado.
2 Associatividade em relação à multiplicação por escalar: multiplicar por um escalar antes ou depois dá o mesmo resultado.
por e por um escalar 
, então o resultado é o mesmo 
e então fazer o produto escalar por . Ou seja,
3 Distributividade em relação à soma: Ou seja
Observação: As propriedades 2 e 3 juntas recebem o nome de linearidade do produto escalar em relação ao primeiro operando.
Observação: Como o produto escalar é comutativo, a linearidade também vale para o segundo operando. Ou seja,
4 Definido positivo: o produto escalar de um vetor não nulo consigo mesmo é sempre positivo.
Resumir com IA:
Gostou desse artigo? Deixe uma nota!
Loading...
