Bem-vindo à nossa seção de problemas resolvidos sobre áreas. Aqui, apresentamos soluções detalhadas para problemas envolvendo o cálculo de áreas de figuras geométricas planas. Vamos explorar o uso de fórmulas e métodos específicos para encontrar a área de triângulos, quadrados, círculos, retângulos e outras figuras.
Cada problema resolvido trará uma explicação passo a passo da estratégia utilizada, desde a identificação dos dados fornecidos até a aplicação correta da fórmula correspondente. Esses exemplos práticos vão ajudar você a desenvolver uma base sólida no cálculo de áreas e a entender a relevância dessas medidas em diversas situações do dia a dia.
Acompanhe-nos nessa jornada educativa e fortaleça seus conhecimentos em geometria. Com prática e compreensão, você ganhará confiança para resolver com sucesso qualquer problema que envolva o cálculo de áreas.
Encontre a diagonal, o perímetro e a área do quadrado:
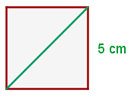
1 Calculamos a diagonal usando o Teorema de Pitágoras
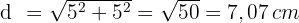
2 Calculamos o perímetro
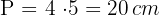
3 Calculamos a área
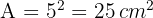
Encontre a diagonal, o perímetro e a área do retângulo:
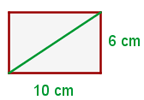
1 Calculamos a diagonal usando o Teorema de Pitágoras
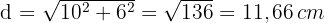
2 Calculamos o perímetro
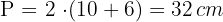
3 Calculamos a área
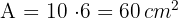
Encontre o perímetro e a área do trapézio retângulo:
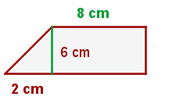
1 Calculamos o lado que falta do triângulo, usando o Teorema de Pitágoras
2 Calculamos o perímetro somando os lados da figura
3 Calculamos a área
Encontre o perímetro e a área do trapézio isósceles:
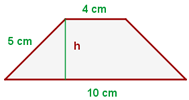
1 Calculamos a altura da figura, usando o Teorema de Pitágoras
2 Calculamos o perímetro somando os lados da figura
3 Calculamos a área
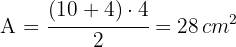
Encontre o perímetro a área do triângulo equilátero:
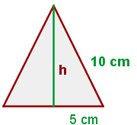
1 Calculamos a altura da figura, usando o Teorema de Pitágoras
2 Calculamos o perímetro da figura
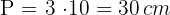
3 Calculamos a área
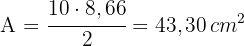
Encontre o perímetro e a área do pentágono regular:
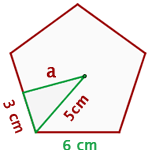
1 Calculamos o valor do apótema, utilizando o Teorema de Pitágoras:
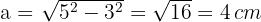
2 Calculamos o perímetro do pentágono:
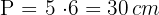
3 Calculamos a área
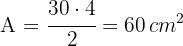
Calcule a área de um hexágono inscrito em uma circunferência de 
cm de raio.
1 . Representamos a figura com os dados fornecidos, observando que, ao traçarmos segmentos do centro aos vértices, obtemos triângulos equiláteros. Assim, o lado do hexágono mede cm
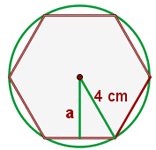
2 Calculamos o valor do apótema, utilizando o Teorema de Pitágoras
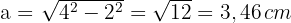
3 Calculamos o perímetro do hexágono:
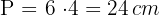
4 Calculamos a área do hexágono:
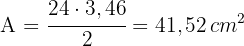
Calcule a área de um quadrado inscrito em uma circunferência de 
cm de raio
1 Representamos a figura com os dados fornecidos, observando que, ao traçarmos segmentos do centro até dois vértices consecutivos, obtemos um triângulo retângulo.
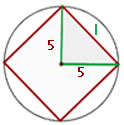
2 Calculamos o valor do lado do quadrado, utilizando o Teorema de Pitágoras:
3 Calculamos a área do quadrado:
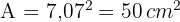
Calculaea área de um triângulo equilátero inscrito em uma circunferência de raio 
cm
1 . Representamos a figura com os dados fornecidos
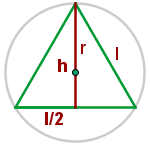
2 O centro da circunferência é o baricentro do triângulo. Portanto:
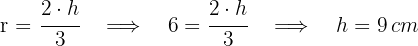
3 Calculamos o lado do triângulo utilizando o Teorema de Pitágoras:
4 Calculamos a área do triângulo
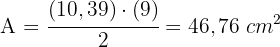
Determine a área do quadrado inscrito em uma circunferência de comprimento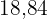 
m.
1 Representamos a figura com os dados fornecidos, observando que, ao traçarmos segmentos do centro até dois vértices consecutivos, obtemos um triângulo retângulo com catetos iguais ao raio da circunferência.
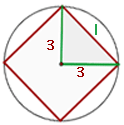
2 Calculamos o raio a partir do comprimento da circunferência:
3Encontramos o lado do quadrado utilizando o Teorema de Pitágoras:
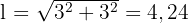
4 Calculamos a área do quadrado:
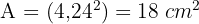
Em um quadrado de 
m de lado, inscrevemos um círculo. Dentro desse círculo, inscrevemos outro quadrado, e dentro dele, mais um círculo. Vamos calcular a área entre esse último quadrado e o último círculo.
1 Representamos a figura com os dados fornecidos.
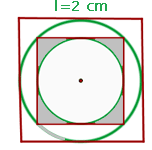
2 O raio do primeiro círculo inscrito é metade do lado do quadrado, ou seja: 
.
A diagonal do segundo quadrado é igual ao diâmetro do primeiro círculo, que mede 
. Usando o Teorema de Pitágoras, vamos calcular o lado desse segundo quadrado:
3 Calculamos a área do segundo quadrado:
4 O raio do segundo círculo é a metade do lado do segundo quadrado. Vamos calcular a área desse círculo:
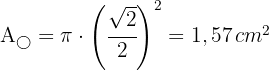
5A área pedida é:
O perímetro de um trapézio isósceles é 
m. As bases medem 
e 
m respectivamente. Calcule os lados não paralelos (iguais) e a área desse trapézio.
1 Representamos a figura com os dados fornecidos
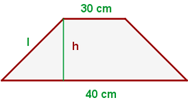
2 Sabemos que o perímetro é a soma de todos os lados. Assim:
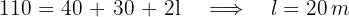
3 Encontramos a altura usando o Teorema de Pitágoras:
4 A área é dada por:
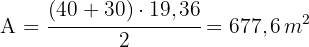
Se prolongarmos os lados não paralelos de um trapézio isósceles, formamos um triângulo equilátero com cm de lado. Sabendo que o trapézio tem metade da altura desse triângulo, calcule a área do trapézio.
1 Com base nas informações, sabemos que a base maior é de 
e a menor é metade disso, ou seja, 
2 Calculamos a altura do triângulo usando o Teorema de Pitágoras
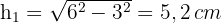
3 A altura do trapézio é metade da altura do triângulo:
4 A área solicitada é
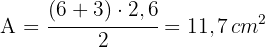
A área de um quadrado é 
. Calcule a área do hexágono regular que tem o mesmo perímetro.
1 Calculamos o valor do lado do quadrado a partir da sua área
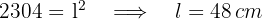
2 Calculamos o perímetro do quadrado
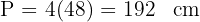
3 O perímetro do hexágono é 
, já que o lado do hexágono é de 
4 Representamos a figura do hexágono com os dados obtidos e calculamos o apótema
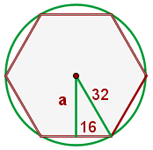
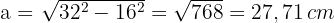
5 Calculamos a área do hexágono
Em uma circunferência de raio igual a m inscreve-se um quadrado. Sobre os lados desse quadrado, voltados para fora, são construídos triângulos equiláteros. Calcule a área da estrela formada.
1 Representamos a figura com base nas informações fornecidas.
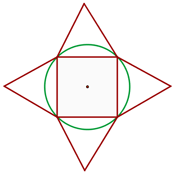
2 Calculamos o lado do quadrado, sendo que a diagonal do quadrado é igual ao diâmetro da circunferência:
3 Encontramos a altura de um triângulo equilátero usando o Teorema de Pitágoras
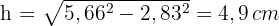
4 A área de um dos triángulo é:
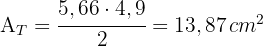
5 A área do quadrado é:
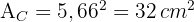
6 A área total da estrela é:
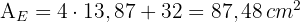
Um hexágono regular com cm de lado tem uma circunferência inscrita e outra circunscrita. Calcule a área da coroa circular formada entre as duas.
1 Representamos a figura com base nos dados fornecidos.
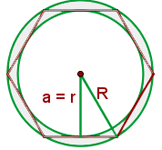
2 O raio da circunferência externa (circunscrita) é igual ao lado do hexágono, ou seja,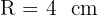 
.
O raio da circunferência interna (inscrita) é o apótema, calculado com o Teorema de Pitágoras:
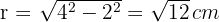
3 A área da coroa circular (diferença entre as áreas dos dois círculos) é:
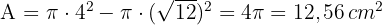
Em uma circunferência, uma corda de 
cm está a 
cm do centro. Calcule a área do círculo.
1 Representamos a figura com as informações dadas.
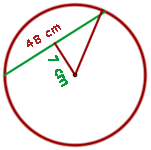
2 Vamos obter o raio da circunferência usando o Teorema de Pitágoras
3 A área do círculo é:
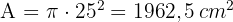
Os catetos de um triângulo retângulo inscrito em uma circunferência medem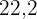 
cm e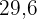 
cm respectivamente. Calcule a medida da circunferência e a área do círculo.
1 Representamos a figura com os dados fornecidos.
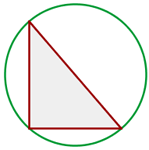
2 A hipotenusa do triângulo é o diâmetro da circunferência. Usamos o Teorema de Pitágoras:
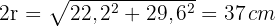
3 O comprimento da circunferência é:
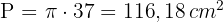
3 A área do círculo é:
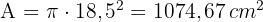
Calcule a área da coroa circular determinada pelas circunferências inscrita e circunscrita a um quadrado de 
m de diagonal.
1 Representamos a figura com base nas informações dadas.
2 O raio da circunferência circunscrita é metade da diagonal do quadrado: 
. O raio da circunferência inscrita é metade do lado do quadrado e lado do quadrado é obtido pelo Teorema de Pitágoras:
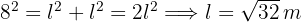
3 A área da coroa circular é a diferença entre as áreas dos dois círculos:
Sobre um círculo de cm de raiotraça-se um ângulo central de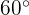 
. Determine a área do segmento circular compreendido entre a corda que une as extremidades dos dois raios e o arco correspondente.
1 Representamos a figura com os dados fornecidos.
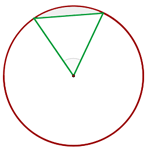
2 Calculamos a área do setor:
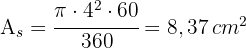
3 O triângulo formado é equilátero, e sua altura pode ser calculada usando o Teorema de Pitágoras:
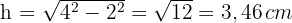
4 Calculamos a área do triângulo:
5 A área solicitada é a diferença entre a área do setor e a do triângulo:
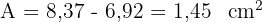
Dado um triângulo equilátero de m de lado, determine a área de um dos setores formados pela circunferência circunscrita e pelos raios que passam pelos vértices.
1 epresentamos a figura com os dados fornecidos.
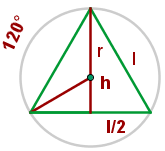
2 Calculamos a altura do triângulo usando o Teorema de Pitágoras:
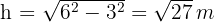
3 O centro da circunferência é o baricentro. Logo, o raio é:
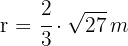
4 Calculamos a área do setor de 
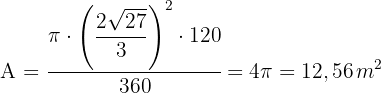
Encontre a área de um quadrilátero convexo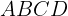 
de perímetro 
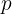com circunferência circunscrita 
de raio 
.
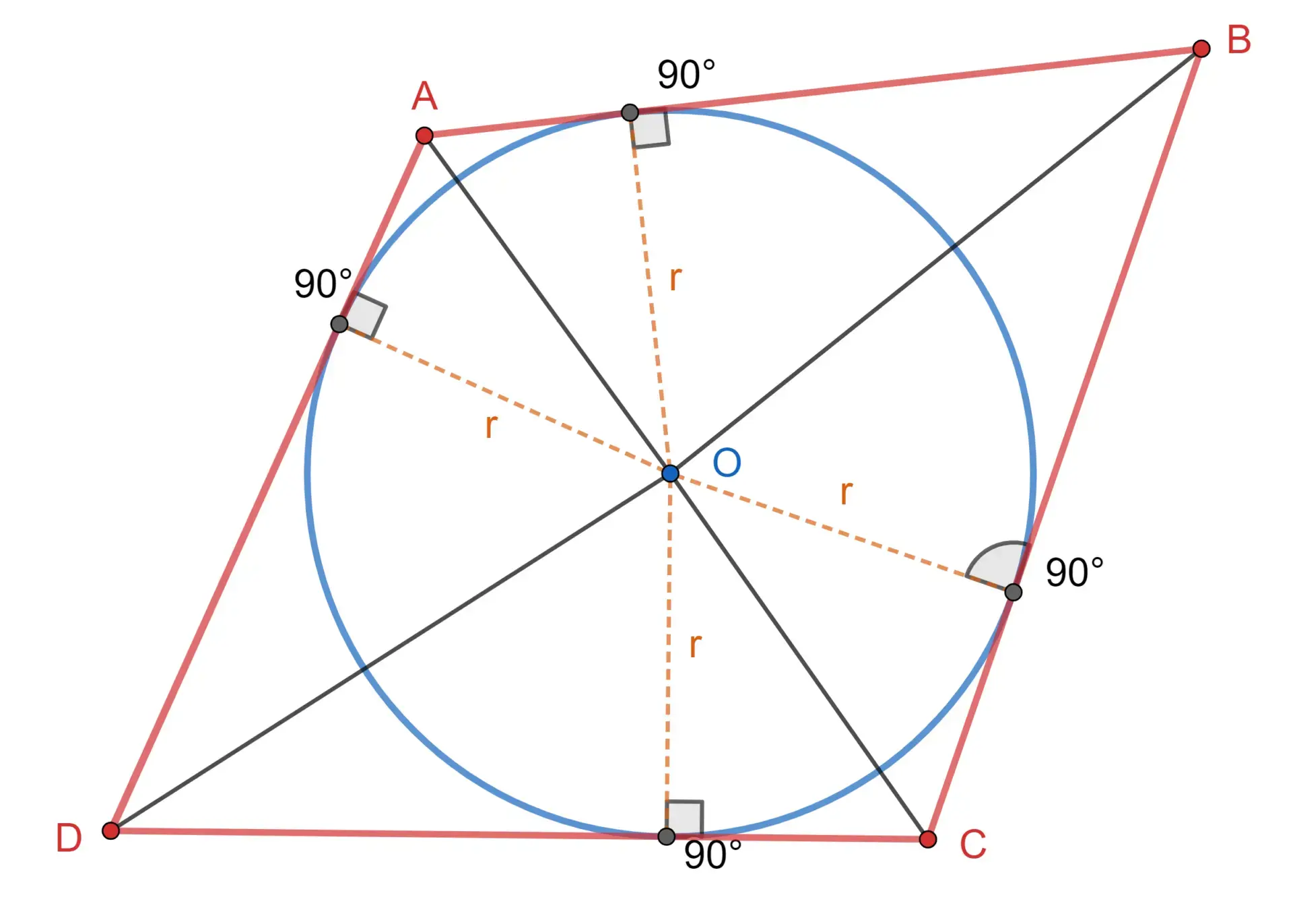
1 Representamos os dados em uma imagem.
2
Note que a área do quadrilátero pode ser decomposta em 4 triângulos com vértice comum no centro da circunferência. Cada triângulo tem área igual a metade do produto entre o raio (altura) e o lado correspondente (base). Assim:
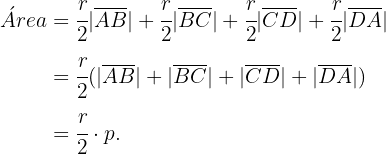
Resolva os seguintes problemas:
1 Encontre a área de um quadrilátero convexo de perímetro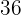 
e circunferência circunscrita 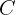de raio 
.
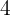2 Encontre a área de um quadrilátero convexo 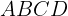de perímetro 
e circunferência circunscrita 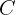de raio 
.
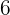Usando a fórmula do exercício 22
1. A área é calculada mediante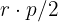 
, em que 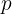é o perímetro, e o raio da circunferência. Assim:
.
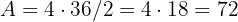2 Para o segundo caso, vamos obter:
.
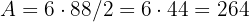Encontre a área de um quadrilátero convexo de lados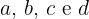 
.
1 Representação das informações em imagem:
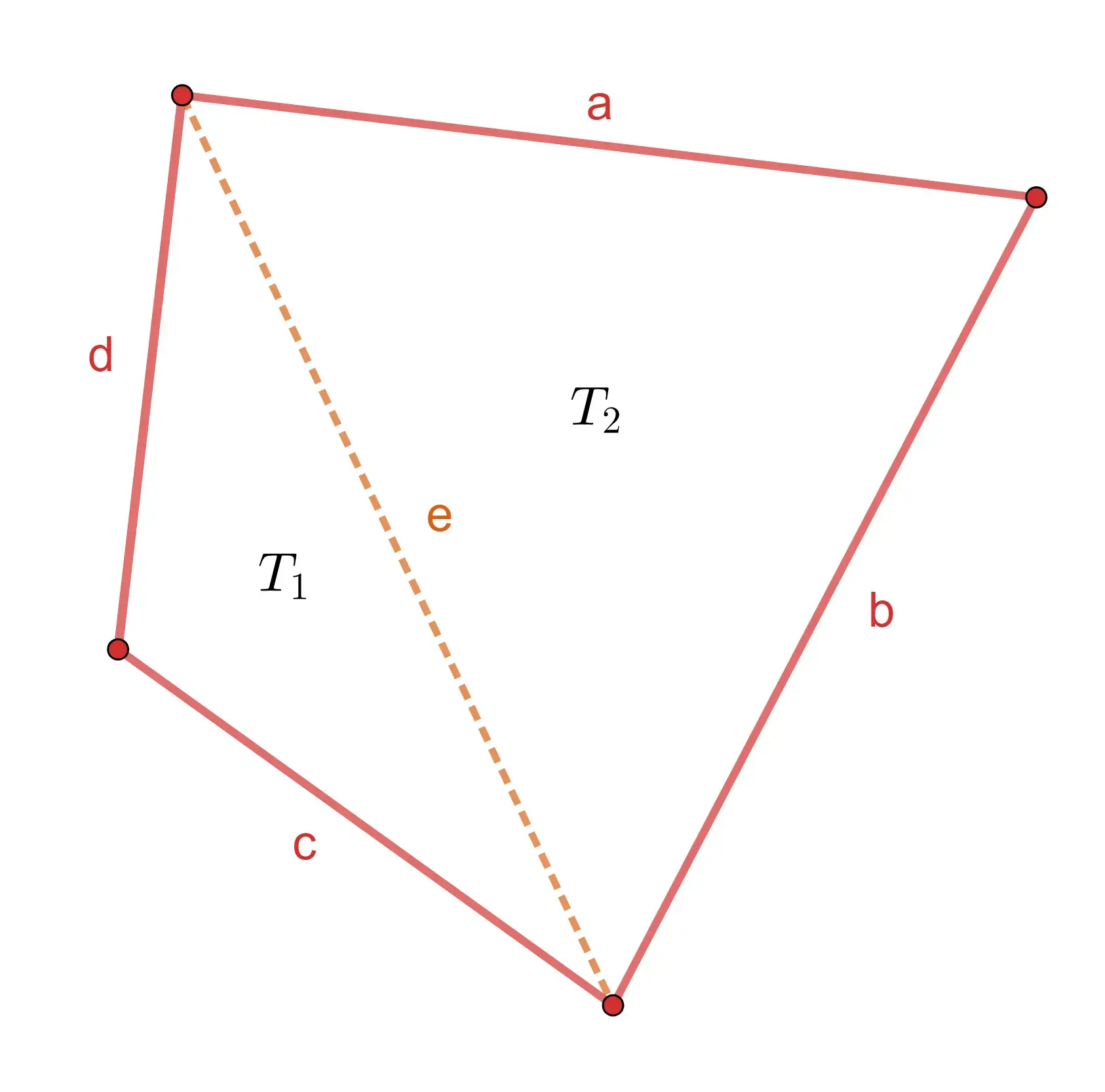
2 Agora, observamos que podemos dividir a figura em dois triângulos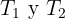 
. Para cada um, utilizamos o Teorema (ou fórmula) de Herão . O semiperímetro de cada triângulo é:
Portanto, suas áreas são:
A área total do quadrilátero será:
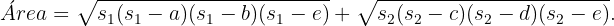
Encontre a área de uma Triquetra:
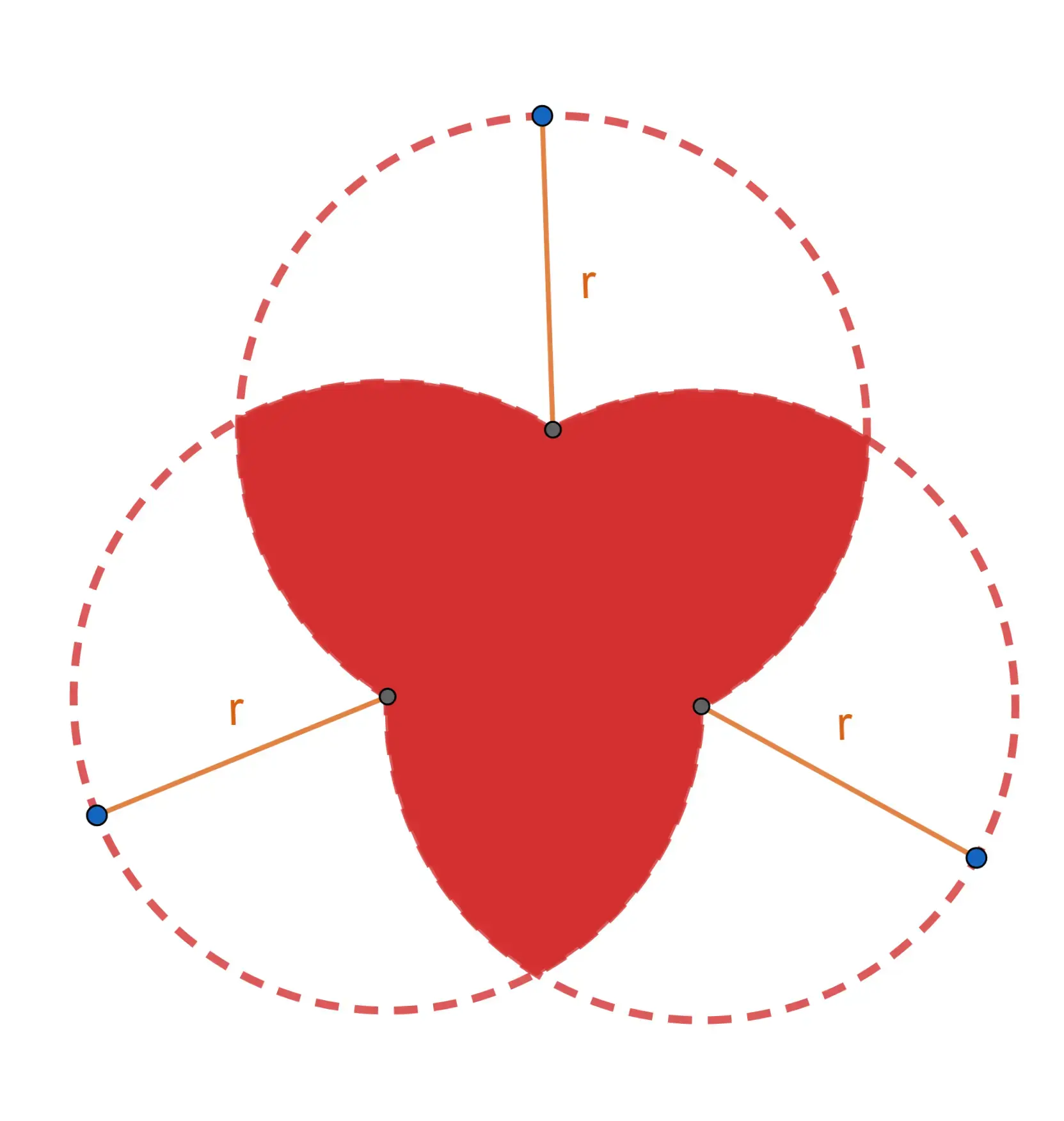
1 Acrescentamos mais linhas à figura para simplificar o cálculo da área de uma triquetra:
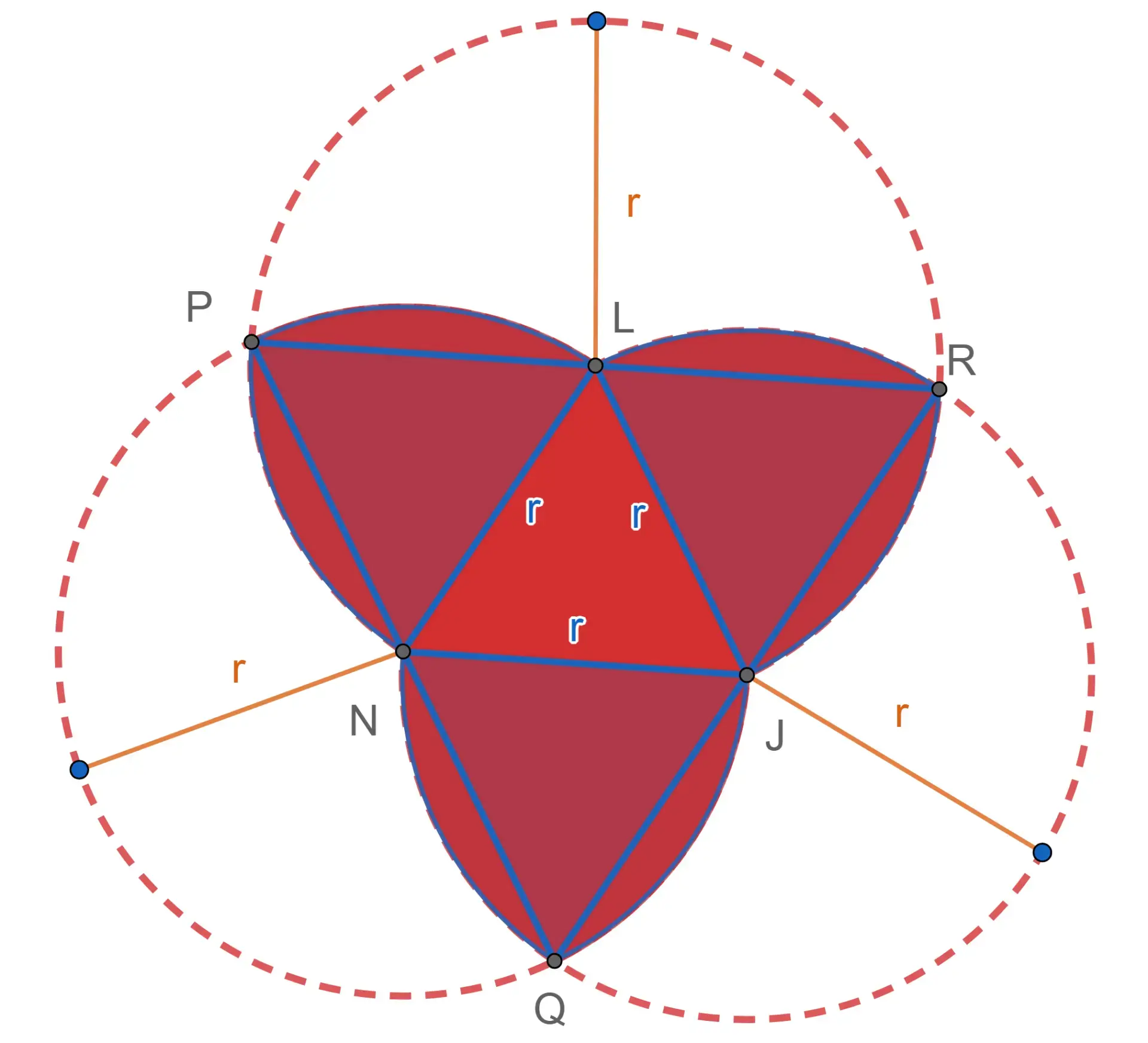
2 Observamos que a área pode ser dividida em duas partes: um triângulo equilátero de lado, de diâmetro de um círculo, ou seja,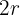 
, e seis setores circulares. A área do triângulo é:
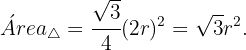
Os setores circulares tem uma área que depende do ángulo. Como neste caso, os ângulos são todos iguais e correspondem a um triângulo equilátero, e seu ângulo é de 
rad. Portanto, a área é cada um é:
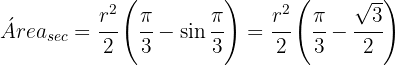
Então, multiplicamos por 6 que é quantidade de setores e somamos com a área do triângulo, para obter a área total da triquetra:
Gostou desse artigo? Deixe uma nota!
Loading...
