A circunferência e o círculo são conceitos fundamentais da geometria, essenciais tanto no estudo teórico da matemática quanto em aplicações práticas. A circunferência é definida como o conjunto de pontos que estão a uma distância fixa, chamada de raio, em relação a um ponto central. Por sua vez, o círculo é a região delimitada pela circunferência e contém todos os pontos que se encontram a uma distância menor ou igual ao raio.
Tanto o círculo quanto a circunferência estão presentes na natureza e no cotidiano, desde o formato dos planetas e órbitas até estruturas arquitetônicas, rodas e muitos mecanismos de precisão. Por isso, compreender suas propriedades e aprender a calcular medidas como o comprimento, a área, os diâmetros e os arcos é muito valioso para desenvolver uma compreensão sólida da geometria.
Encontre o comprimento de uma circunferência cujo raio mede 5,3 cm
1Vamos recordar que a fórmula do comprimento (ou perímetro) de uma circunferência é:
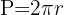
2Substituímos os dados conhecidos e obtenemos
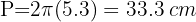
Calcule a área de um círculo com raio de 11 cm.
1Vamos relembrar a fórmula para a área de um círculo:

2Substituímos os dados conhecidos e obtenemos:
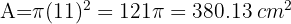
Encontre o comprimento de um arco de 100° em uma circunferência de raio 9 cm
1Relembre que a fórmula do comprimento de um arco de uma circunferência é:
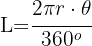
2Substituímos os dados conhecidos e obtemos:
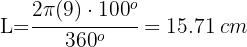
Em uma circunferência de raio 10 cm, um arco mede 15 cm. Qual é o ângulo central subtendido por esse arco?
1Recordando a fórmula do comprimento do arco da circunferência é:
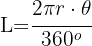
2Substituímos os dados conhecidos, isolamos o ângulo e obtemos:
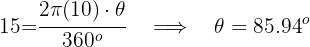
Encontre a área de um setor circular com ângulo central de 60° e raio de 7 cm.
1Relembre que a fórmula da área de um setor circular é:
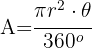
2Substituímos os dados conhecidos e obtemos:
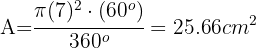
Se o comprimento de uma circunferência é 70 cm, encontre seu diâmetro.
1Lembrando a fórmula da área de um círculo de uma circunferência é:
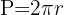
2Substituímos os dados conhecidos, isolamos o raio e obtemos:
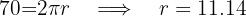
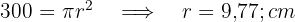
Portanto, o diâmetro é:
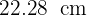
Se a área de um círculo é 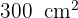 , encontre seu diâmetro.
, encontre seu diâmetro.
1Relembrando a fórmula da área de um círculo:

2Substituíimos os dados conhecidos, isolamos o raio e obtemos:
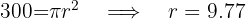
Dessa forma, o diâmetro é igual a 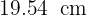
Em uma circunferência de raio 17 cm, dois pontos A e B estão separados por um ângulo de 80° em relação ao centro. Qual é a distância entre A e B medida sobre a circunferência?
1Relembrando a fórmula para o comprimento de arco:
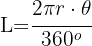
2Substituímos os dados conhecidos e obtemos:
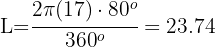
Assim, a distância de A até B sobre a circunferência 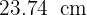
Encontre a distância do ponto (7,2) até a circunferência com centro na origem (0,0) e raio 3
1Calculamos a distância entre o ponto e o centro da circunferência:
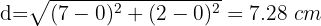
2Em seguida, subtraímos o raio para obter a distância até a circunferência:
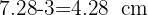
Os braços de um balanço medem 1,8 m de comprimento e podem abrir, no máximo, um ângulo de 146°. Calcule o espaço percorrido pelo assento do balanço quando o ângulo descrito no seu movimento de balanço é o máximo.
1Calculamos s o comprimento do arco correspondente a 
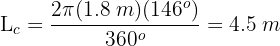
A roda de um caminhão tem 90 cm de raio. Quanto o caminhão percorreu após a roda dar 100 voltas?
1Convertendo o raio para metros:

2Calculando a distância percorrida em uma volta:
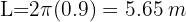
3Calculando a distância para 100 voltas:

Um farol varre com sua luz um ângulo plano de 128°. Se o alcance máximo do farol é de 7 milhas, qual é o comprimento máximo, em metros, do arco correspondente?
1Convertendo o raio para metros, sabendo que 1 milha equivale a 1609.34 metros
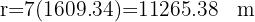
2Calculamos o comprimento do arco  :
:
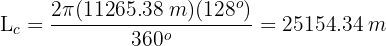
O comprimento de uma circunferência é 43,96 cm. Qual é a área do círculo?
1Calculamos o raio da circunferência

2Calculamos a área do círculo
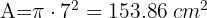
A área de um setor circular de 90° é 4π cm². Calcule o raio do círculo ao qual pertence e o comprimento da circunferência.
1Calculamos o raio do setor:
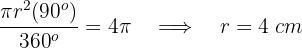
2Calculamos o comprimento da circunferência:
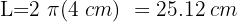
Ana subiu no cavalo que está a 3,5 m do centro de uma plataforma giratória, e sua amiga Laura subiu no leão que está a 2 m do centro. Calcule a distância percorrida por cada uma após 50 voltas da plataforma.
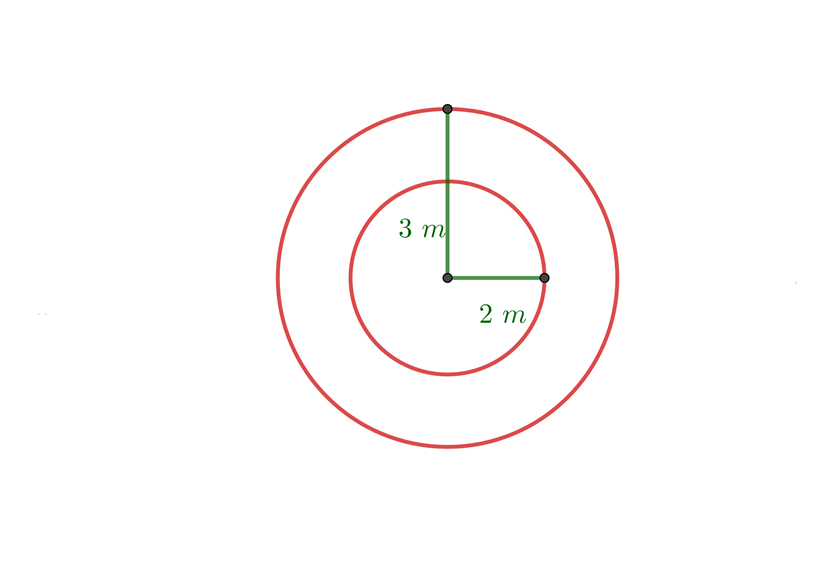
1Calculamos a distância percorrida em uma volta com 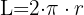


2:O percurso total é obtido multiplicando por 50 voltas
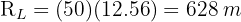

Calcule a área de um setor circular cuja corda é o lado de um triângulo equilátero inscrito, sendo 2 cm o raio da circunferência

1O setor descrito corresponde a um terço da área total do círculo, ou seja, um setor de 
2Calculamos a área para 

Dadas duas circunferências concêntricas de raios 8 cm e 5 cm, traçam-se os raios OA e OB que formam um ângulo de 60°. Calcule a área do trapézio circular formado.

1Calculamos a área dos dois setores e depois a diferença entre eles:

Em um parque de forma circular com 700 m de raio, há situada no centro uma fonte, também de forma circular, com 5 m de raio. Calcule a área da zona de passeio.

1Calculamos a área dos dois círculos e subtraímos:
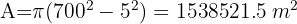
A superfície de uma mesa é formada por uma parte central quadrada de 1 m de lado e dois semicírculos nos lados opostos. Calcule a área.

1Calculamos a área do quadrado e do círculo formado pelos dois semicírculos, depois somamos:
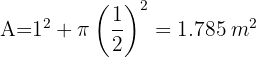
Encontre a área do setor circular cuja corda é o lado do quadrado inscrito, sendo o raio da circunferência 4 cm.

1Calculamos a área para o setor de 
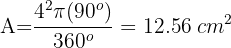
Calcule a área sombreada, sabendo que o lado do quadrado mede 6 cm e o raio do círculo mede 3 cm.

1Calculamos a área do quadrado e do círculo, depois subtraímos:

Em uma praça circular com raio de 250 m serão instalados 7 postes de luz, cujas bases são círculos com 1 m de raio. O restante da praça será coberto com grama. Calcule a área destinada à grama.

1Calculamos a área da praça, das bases dos postes e subtraímos:

Calcule a área da parte sombreada, se o raio do círculo maior é 6 cm e o dos círculos menores é 2 cm.
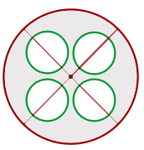

1Calculamos a área do círculo maior, dos círculos menores, depois subtraímos:
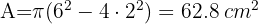
Calcule a área sombreada, sendo AB = 10 cm, ABCD um quadrado e APC e AQC arcos de circunferência com centros em B e D.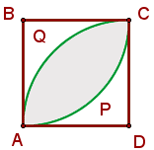
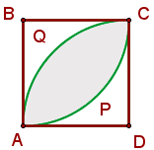
1 A parte sombreada é formada por dois segmentos circulares:
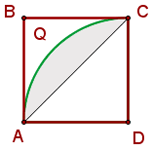
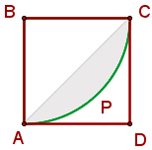
2Calculamos a área do segmento circular e multiplicamos por 2
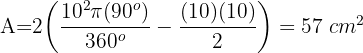
Em um hexágono regular de 4 cm de lado, inscreve-se uma circunferência e outra circunferência é circunscrita. Calcule a área da coroa circular formada.

1Calculamos o raio da circunferência interior que coincide com a apótema do hexágono:

2Calculamos as áreas de cada círculos e subtraímos:
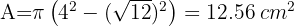
Em uma circunferência, uma corda mede 48 cm e está distante 7 cm do centro. Calcule a área do círculo.
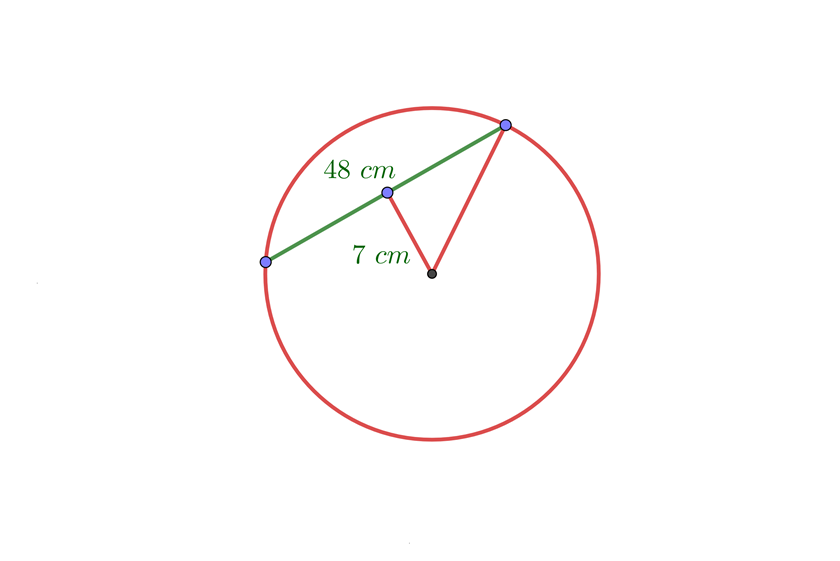
1Calculamos o raio do círculo aplicando o Teorema de Pitágoras
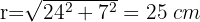
2Calculamos a área do círculo:
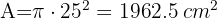
Os catetos de um triângulo inscrito em uma circunferência medem 22,2 cm e 29,6 cm. Calcule a área da circunferência.

1Calculamos a hipotenusa, que corresponde ao diâmetro da circunferência:
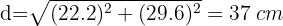
2Calculamos a área de cada círculo
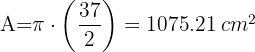
Em um círculo de 4 cm de raio, traça-se um ângulo central de 60°. Calcule a área do segmento circular compreendido entre a corda que une os extremos dos dois raios e o seu arco correspondente.

1Calculamos a área do setor:
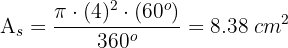
2Calculamos Calculamos a altura do triângulo e sua área:


3Calculamos a diferença entre as duas áreas através da subtração.
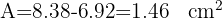
Considerando um triângulo equilátero de lado 6 m, calcule a área de um setor determinado pela circunferência circunscrita e pelos raios que passam pelos vértices.
1O centro da circunferência é o baricentro, então:

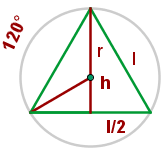
2Calculamos a altura do triângulo e o raio:
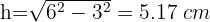

3Calculamos a área do setor
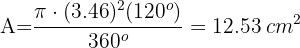
Calcule a área da coroa circular determinada pelas circunferências inscrita e circunscrita a um quadrado de diagonal 8 m.

1Calculamos o raio do círculo exterior, cujo diâmetro é a diagonal do quadrado, e o raio do círculo interior usando o Teorema de Pitágoras.
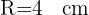

2Calculamos a diferença das áreas:
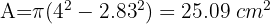
Resumir com IA:


