Seja bem-vindo à sua página dedicada aos problemas e exercícios resolvidos da equação da hipérbole!
Aqui, vamos explorar as características dessa curva fascinante que está no coração da geometria analítica. Também, desvendaremos o passo a passo diversos problemas envolvendo a equação da hipérbole, para que você possa compreender e dominar profundamente essa forma geométrica.
Além disso, vamos guiar você por exemplos práticos e exercícios resolvidos que vão te ajudar a construir um entendimento sólido sobre hipérboles. Seja você um estudante se preparando para provas e ENEM ou um curioso desvendando as maravilhas dessas curvas fascinantes, esta página será seu guia completo! Prepare-se para mergulhar no mundo intrigante das equações da hipérbole!
Determine a equação da hipérbole com foco  , vértice
, vértice  e centro
e centro 
1 Como o centro e o vértice se encontram sobre o eixo horizontal, então a equação é da forma.

2 Calculamos o valor de  , o qual é igual à distância do centro a um dos seus vértices
, o qual é igual à distância do centro a um dos seus vértices

3 Calculamos o valor de  , o qual é igual à distância do centro a um dos seus focos
, o qual é igual à distância do centro a um dos seus focos

4 Calculamos o valor de 
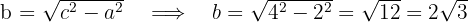
5 A equação da hipérbole é:

Determine a equação da hipérbole com foco  , vértice
, vértice  e centro
e centro 
1 Como o centro e o vértice estão sobre o eixo vertical, a equação é da forma:

2 Calculamos o valor de  o qual é igual à distância do centro a um dos vértices.
o qual é igual à distância do centro a um dos vértices.

3 Calculamos o valor de  o qual é igual à distância do centro a um dos focos.
o qual é igual à distância do centro a um dos focos.

4 Calculamos o valor de  :
:
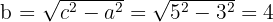
5 A equação da hipérbole é:

Encontre a equação da hipérbole com foco  , vértice
, vértice  e centro
e centro 
1 Como o centro e o vértice têm a mesma coordenada  , então a equação é da forma:
, então a equação é da forma:
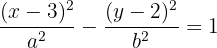
2 Calculamos o valor de  , que é igual à distância do centro a um dos vértices
, que é igual à distância do centro a um dos vértices
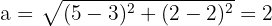
3 Calculamos o valor de  , que é igual à distância do centro a um dos focos
, que é igual à distância do centro a um dos focos
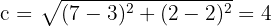
4 Calculamos o valor de 

5 A equação da hipérbole é
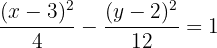
Encontre a equação da hipérbole com foco  , vértice
, vértice  e centro
e centro 
1 Como o centro e o vértice têm a mesma coordenada  , então a equação é da forma
, então a equação é da forma
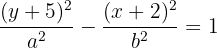
2 Calculamos o valor de  , que é igual à distância do centro a um dos vértices
, que é igual à distância do centro a um dos vértices
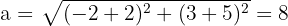
3 Calculamos o valor de  , que é igual à distância do centro a um dos focos
, que é igual à distância do centro a um dos focos
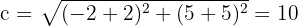
4 Calculamos o valor de 

5 A equação da hipérbole é
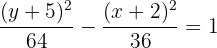
Encontre a equação e a excentricidade da hipérbole que tem como focos os pontos 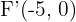 e
e  com diferença das distâncias aos focos igual a
com diferença das distâncias aos focos igual a  .
.
1 Como estão sobre o eixo horizontal e são simétricos em relação à origem, então o centro é  e a equação é da forma:
e a equação é da forma:

2 Calculamos o valor de  , que é igual à distância do centro a um dos focos:
, que é igual à distância do centro a um dos focos:
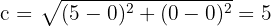
3 Como a diferença dos raios vetores é  , então:
, então:
 , logo
, logo 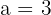
4 Calculamos o valor de 

5 A equação da hipérbole é:
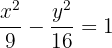
6 A excentricidade é:
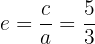
Determine a equação e a excentricidade da hipérbole que tem como focos os pontos 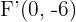 e
e 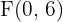 e
e  como diferença dos raios vetores.
como diferença dos raios vetores.
1. Como os focos estão sobre o eixo vertical e são simétricos em relação à origem, então o centro é  e a equação é da forma:
e a equação é da forma:

2 Calculamos o valor de  , que é igual à distância do centro a um dos focos:
, que é igual à distância do centro a um dos focos:

3 Como a diferença dos raios vetores é  , então
, então
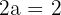 , logo
, logo 
4 Calculamos o valor de: 

5 A equação da hipérbole é:
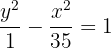
6 A excentricidade é:

Determine as coordenadas dos vértices e dos focos, as equações das assíntotas e a excentricidade da hipérbole 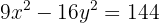
1 Primeiro, vamos escrever a equação da hipérbole na forma reduzida, dividindo os lados por 
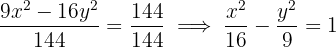
então, 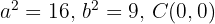
2 Calculamos o valor de 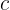
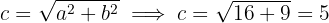
3 As coordenadas dos vértices são:
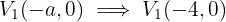
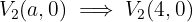
4 As coordenadas dos focos são:
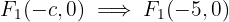
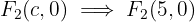
5 As equações das assíntotas são:


6 A excentricidade é:
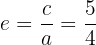
Encontre as coordenadas dos vértices e dos focos, as equações das assíntotas e a excentricidade da hipérbole 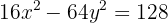
1 Primeiro escrevemos a equação da hipérbole na sua forma reduzida, para isso dividimos ambos os lados por 
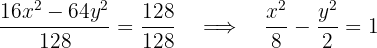
então,  e
e 
2 Calculamos o valor de 

3 As coordenadas dos vértices são:
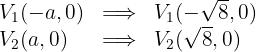
4 As coordenadas dos focos são:
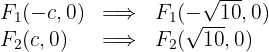
5 As equações das assíntotas são:
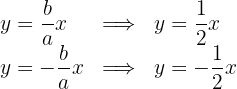
6 A excentricidade é:
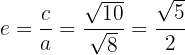
Faça a representação gráfica e determine as coordenadas dos focos, dos vértices e a excentricidade das seguintes hipérboles:
9.1
9.2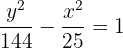
1.1 A equação da primeira hipérbole tem os seguintes valores de 
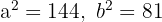 e
e 
1.2 Calculamos o valor de 

1.3 O eixo é horizontal e a hipérbole tem centro na origem, uma vez que as coordenadas dos vértices são:
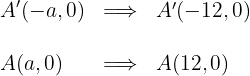
1.4 As coordenadas dos focos são:
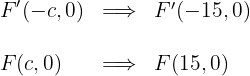
1.5A excentricidade é:

1.6O gráfico é:
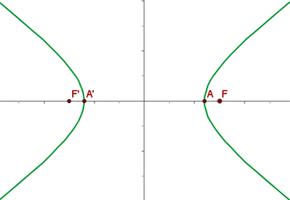
2.1 A equação da segunda hipérbole tem os seguintes valores de 
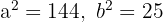 e
e 
2.2Calculamos o valor de 

2.3O Se o eixo real é vertical e a hipérbole tem centro na origem, então as coordenadas dos vértices são:
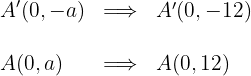
2.4 As coordenadas dos focos são:
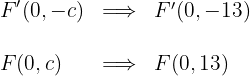
2.5 A excentricidade é:

2.6 O gráfico é:
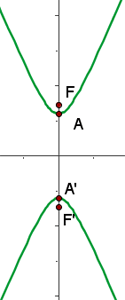
Faça a representação gráfica e determine as coordenadas dos focos, dos vértices e a excentricidade das seguintes hipérboles:
10.1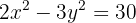
10.2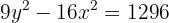
1.1 Na primeira hipérbole, vamos representar a equação de forma reduzida dividindo os dois lados por: 
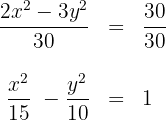
da equação, vamos obter os valores de:  e o centro:
e o centro:
 e
e 
1.2 Calculamos o valor de: 
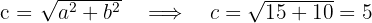
1.3 O eixo real é horizontal e a hipérbole têm centro na origem, uma vez que as coordenadas dos vértices são:
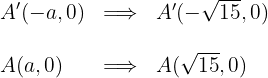
1.4 As coordenadas dos focos são:
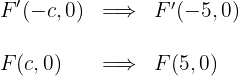
1.5 A excentricidade é:
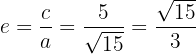
1.6 O gráfico é:
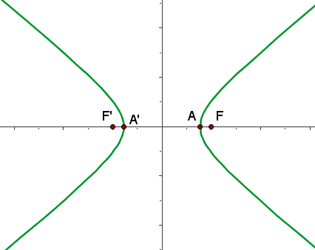
2.1 Na segunda hipérbole, vamos representar a equação de forma reduzida dividindo ambos os lados por 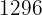
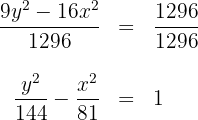
da equação é obtido os valores de  e o centro
e o centro
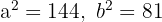 e
e 
2.2 Calculamos o valor de 

2.3 O eixo vertical e a hipérbole têm centro na origem, já que as coordenadas dos vértices são:
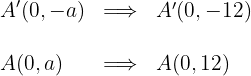
2.4 As coordenadas dos focos são:
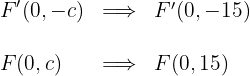
2.5 A excentricidade é:

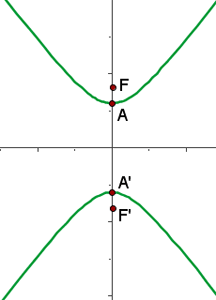
2.6 O gráfico é:
Faça a representação gráfica e determine as coordenadas dos focos, dos vértices e a excentricidade das seguintes hipérboles:
11.1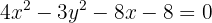
11.2
1.1 Na primeira hipérbole, vamos representar a equação de forma reduzida:
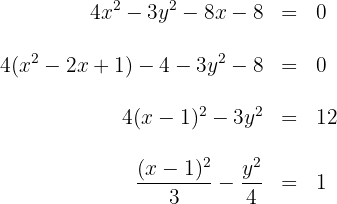
da equação são obtidos os valores de:  e centro:
e centro:
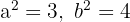 e
e 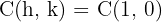
1.2 Calculamos o valor de 
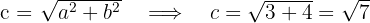
1.3 O eixo real é horizontal e a hipérbole têm centro 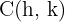 , uma vez que as coordenadas dos vértices são:
, uma vez que as coordenadas dos vértices são:
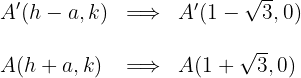
1.4 As coordenadas dos focos são:

1.5 A excentricidade é:
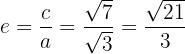
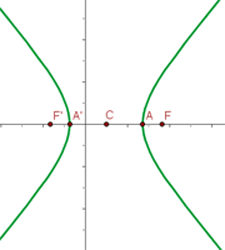
1.6 O gráfico é:
2.1 Vamos representar a segunda hipérbole em sua forma reduzida:
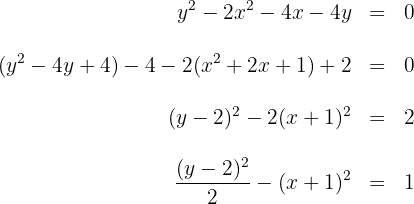
da equação, são obtidos os valores de:  e centro
e centro
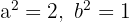 e
e 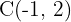
2.2 Calculamos o valor de 
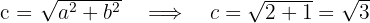
2.3 O eixo é vertical e a hipérbole têm centro em 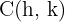 , já que as coordenadas dos vértices são:
, já que as coordenadas dos vértices são:

2.4 As coordenadas dos focos são:

2.5 A excentricidade é:
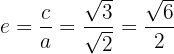
2.6 O gráfico é:
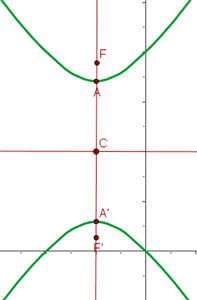
Encontre a equação da hipérbole com um eixo real horizontal  e distância focal
e distância focal 
1 Como o eixo real é igual a 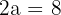 , então,
, então,

2 Como a distância focal é igual a  , então
, então 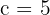
3 Calculamos o valor de 
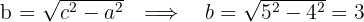
4 Consideramos o centro na origem, já que a equação da hipérbole é:

Encontrar a equação de uma hipérbole de eixo imaginário vertical com semi-eixo imaginário igual a  e distância focal igual a
e distância focal igual a  .
.
1 Como o eixo imaginário mede 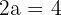 ,
,
então  .
.
2 Como a distância focal é 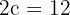 ,
,
então 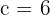 .
.
3 Calculamos o valor de  :
:
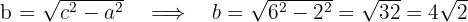
4 Considerando o centro da hipérbole na origem, a equação reduzida é:
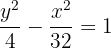
O eixo real de uma hipérbole mede  , é horizontal, tem centro na origem e passa pelo ponto
, é horizontal, tem centro na origem e passa pelo ponto  . Determine a equação.
. Determine a equação.
1 Como o eixo real mede 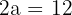 , então
, então  .
.
2 A equação da hipérbole é:
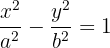
3 Como a hipérbole passa pelo ponto  , substituímos e calculamos o valor de
, substituímos e calculamos o valor de  :
:
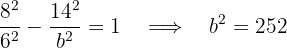
4 Como o centro está na origem, a equação reduzida da hipérbole é:
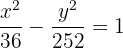
Calcule a equação reduzida da hipérbole com centro na origem, eixo real horizontal, distância focal  e distância de um foco ao vértice mais próximo igual a
e distância de um foco ao vértice mais próximo igual a  .
.
1 Como a distância focal é 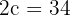 , então
, então 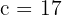 .
.
2 Como a distância de um foco ao vértice mais próximo é 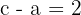 , então
, então 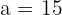 .
.
3 Calculamos  :
:
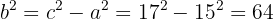
4 Como o centro está na origem, a equação reduzida da hipérbole é:
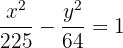
O eixo principal de uma hipérbole é horizontal e mede  , e sua excentricidade é
, e sua excentricidade é  . Determine a equação da hipérbole.
. Determine a equação da hipérbole.
1 Como o eixo principal mede  , então
, então 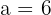 .
.
2 Como a excentricidade é 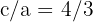 , então
, então 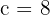 .
.
3 Calculamos  :
:
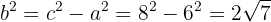
4 Como o centro está na origem, a equação reduzida da hipérbole é:
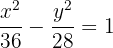
Calcule a equação de uma hipérbole equilátera sabendo que a distância focal é 
1 Como a distância focal é  , então
, então 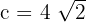
2 Como a hipérbole é equilátera, temos  , e:
, e:

3 Considerando o centro na origem, a equação reduzida da hipérbole é:

O eixo imaginário de uma hipérbole é vertical, mede  e as equações das assíntotas são
e as equações das assíntotas são 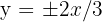 . Determine a equação da hipérbole, seus eixos, focos e vértices.
. Determine a equação da hipérbole, seus eixos, focos e vértices.
1 Como o eixo imaginário mede  , então
, então 
2 Como a inclinação das assíntotas é 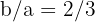 , então
, então 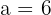
3 Calculamos 

4 Como o centro está na origem, a equação reduzida da hipérbole é:
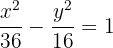
5 As coordenadas dos vértices são:
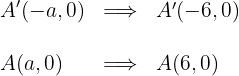
6 As coordenadas dos focos são:
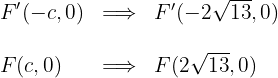
Calcule a equação reduzida de uma hipérbole com eixo real horizontal, centro na origem e que passa pelos pontos 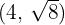 e
e 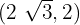
1 A equação da hipérbole é de forma:

2 Como a hipérbole passa pelos pontos 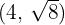 e
e 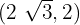 , ao fazer a substituição, é obtido um sistema de equações com termos
, ao fazer a substituição, é obtido um sistema de equações com termos 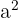 e
e 
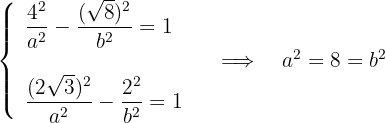
3 A equação da hipérbole é:
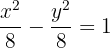
Determine a equação reduzida de uma hipérbole com eixo real horizontal, centro na origem, passa pelos pontos  e excentricidade de
e excentricidade de 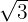
1 A equação da hipérbole é de forma:

2 Como a hipérbole passa pelo ponto  , ao fazer as substituições, é obtido:
, ao fazer as substituições, é obtido:
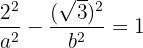
3 Como a excentricidade 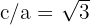 e
e 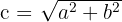 , então, ao fazer a substituição, é obtido:
, então, ao fazer a substituição, é obtido:

4 Temos o seguinte sistema de equações, do qual se obtém
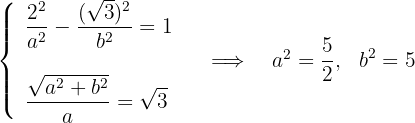
5 A equação da hipérbole é:

Determine a equação reduzida de uma hipérbole com centro na origem, eixo real horizontal e sabendo que um foco está distante dos vértices da hipérbole  e
e 
1 Pelo enunciado, sabemos que o eixo real é igual a 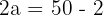 , portanto,
, portanto, 
2 Como a distância focal é igual a 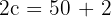 , então
, então 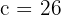
3 Calculamos o valor de 
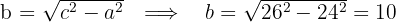
4 Consideramos o centro na origen, já que a equação da hipérbole é:

Determine a posição relativa da reta 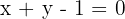 em relação à hipérbole
em relação à hipérbole 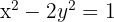
1 Para determinar os pontos de interseção de ambas curvas, vamos isolar a variável,  na reta
na reta 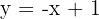 e substituir na hipérbole.
e substituir na hipérbole.
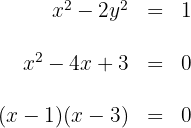
Assim, as raízes são:  e
e 
2 Substituindo os valores de  na equação da reta, vamos obter os pontos de interseção
na equação da reta, vamos obter os pontos de interseção 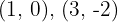
3 O gráfico ficará assim:
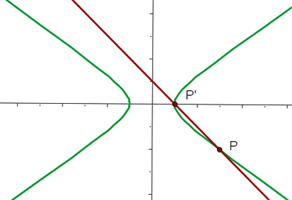
Uma hipérbole equilátera passa pelo ponto 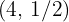 . Encontre a equação referida às suas assíntotas como eixos, e as coordenadas dos vértices.
. Encontre a equação referida às suas assíntotas como eixos, e as coordenadas dos vértices.
1 Determinamos a equação da hipérbole. Para isso, multiplicamos 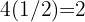 . Assim, a equação da hipérbole equilátera é
. Assim, a equação da hipérbole equilátera é  .
.
2 Sendo a hipérbole equilátera, 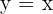 é a reta que contém o eixo real. Os vértices são obtidos resolvendo o sistema de equações:
é a reta que contém o eixo real. Os vértices são obtidos resolvendo o sistema de equações:
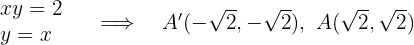
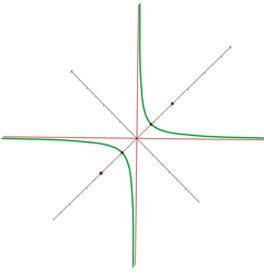
3 O gráfico é dado por:
Determine a equação de uma hipérbole equilátera sabendo que  . Quais as coordenadas dos focos?
. Quais as coordenadas dos focos?
1 Como a hipérbole é equilátera, então  , logo
, logo
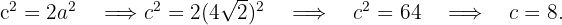
2 Consideramos o centro na origem, portanto a equação da hipérbole é 
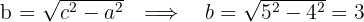
3 Consideramos o centro na origem, portanto a equação da hipérbole é:

4 As coordenadas dos focos são: 
O eixo principal de uma hipérbole é horizontal e mede  , a excentricidade
, a excentricidade  . Calcule a equação da hipérbole.
. Calcule a equação da hipérbole.
1 Como o eixo principal é 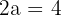 , então
, então 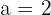
2 Como a excentricidade é 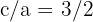 , então
, então 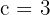
3 Calculamos 
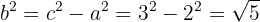
4 Consideramos o centro na origem, portanto a equação da hipérbole é
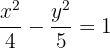
Resumir com IA:


