Bem-vindo à nossa seção dedicada à resolução de equações lineares e suas aplicações práticas. As equações lineares são essenciais na matemática e desempenham um papel fundamental em diversas áreas, como física, economia e até na solução de problemas cotidianos. Neste guia, vamos acompanhar você em um aprendizado que inclui tanto a resolução de equações quanto o uso delas para interpretar situações do dia a dia.
Resolver uma equação linear significa encontrar o valor que torna a equação verdadeira. Esse processo requer atenção ao passo a passa da álgebra e, mais do que isso, ajuda a desenvolver o raciocínio lógico. Além disso, você verá como essas equações podem ser usadas para solucionar questões reais em diferentes contextos.
Dominar o conceito de equações lineares é uma habilidade indispensável, seja na matemática ou em desafios da vida prática. Nesta jornada, você encontrará exercícios e exemplos aplicados que mostram como essa ferramenta pode ajudar a compreender e resolver situações que encontramos no nosso cotidiano.

Exercícios práticos
1) Fazemos a multiplicação dos dois lados da equação: 2) Em seguida, fazemos a soma e a subtração dos termos semelhantes nos dois lados: 3) Para descobrir X, primeiro somamos 40 nos dois lados e então, simplificamos: 4) Para obter X, agora multiplicamos por Dessa forma, x = 7 é o resultado dessa equação 1) Fazemos a multiplicação: 2) Somamos e subtraímos os termos semelhantes nos dos lados da equação 3) Para descobrir X, primeiro subtraímos X e 8, dos dois lados da equação e simplificamos: 4) Para obter X, multiplicamos por Logo, a solução da equação é: x = 1 1) Calculamos o 2) Multiplicamos os dois lados pelo 3) Somamos e subtraímos os termos semelhantes: 4) Para descobrir o x, primeiro resolvemos 4x e depois somamos 4 e vamos obter: Para obter x, vamos multiplicar por Assim, a resposta da equação é x = 6 1) Realizamos a multiplicação e simplificamos as frações: 2) Calculamos o 3)Multiplicamos os dois lados pelo 4) Fazemos a adição e a subtração dos termos semelhantes: 5) Para descobrir X, multiplicamos por Desta forma, a solução para essa equação é: Multiplicamos ambos os lados da equação por x - 3 e x - 2 e obtemos: 2) Fazemos a multiplicação: 3) Adicionamos 4x e subtraímos 15 dos dois lados: Portanto, a resposta para essa equação é x = 7 1) Tiramos os colchetes: 2) Calculamos o 3) Multiplicamos pelo 4) Somamos e subtraímos os termos semelhantes: 5) Retiramos 30x e 3 dos dois lados: 6) Multiplicamos os dois lados da equação por Logo, o resultado da equação é x = 3 1) Resolvemos usando a fórmula para encontrar a raiz quadrada de uma equação de segundo grau: E as raízes quadradas são: As raízes da equação são os resultados buscados. Desta forma, x = 1 e x = - 4. 1) Resolvemos empregando a fórmula para encontrar a raiz quadrada de uma equação de segundo grau: Como nos números reais não existem raízes de números negativos, concluímos que a equação não possui soluções reais. 1) Resolvemos empregando a fórmula para encontrar a raiz quadrada de uma equação de segundo grau: As raízes são: Como o resultado das raízes são os mesmos das equações, os resultados são: 1) Resolvemos usando a fórmula para encontrar a raiz quadrada de uma equação de segundo grau: As raízes são essas: Como o resultado das raízes são os mesmos das equações, portanto: x = - 2 e x = 2![]()



![]() nos dois lados da equação e simplificamos:
nos dois lados da equação e simplificamos:
![]()


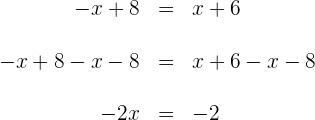
![]() nos dois lados da equação:
nos dois lados da equação:
![]()
![]()

![]()

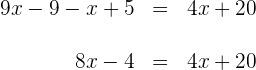
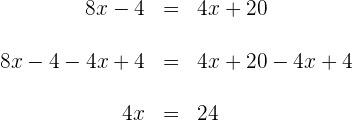
![]() os dois lados da equação:
os dois lados da equação: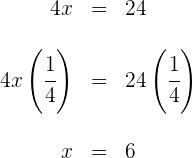
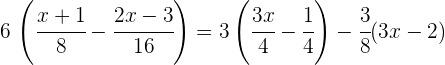
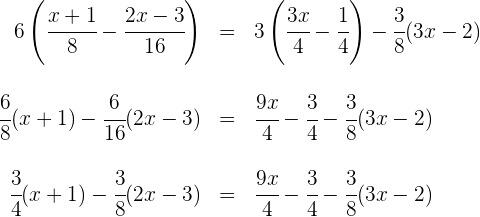
![]() dos denominadores:
dos denominadores: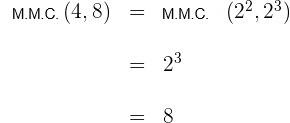
![]()
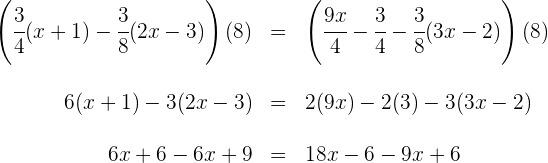
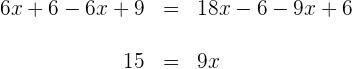
![]() os dois lados da equação e obtemos
os dois lados da equação e obtemos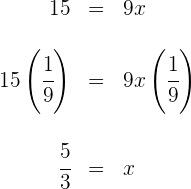
![]()
![]()
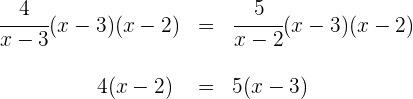
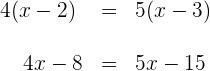
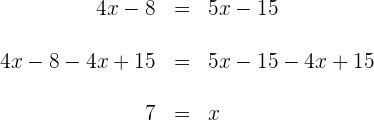
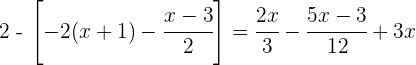
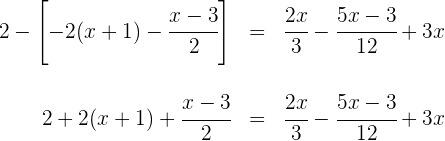
![]() dos denominadores:
dos denominadores: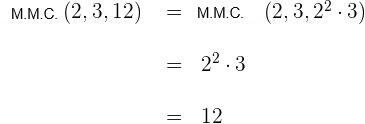
![]()


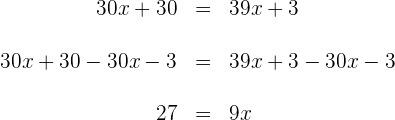
![]() :
: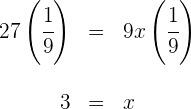
![]()

![]()
![]()
![]()
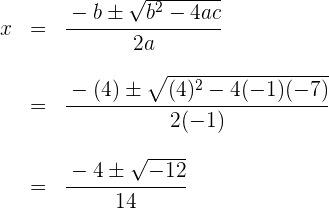
![]()
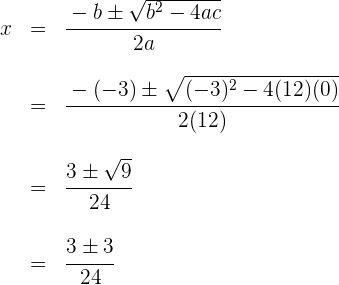
![]()
![]()
![]() e
e ![]()
![]()

![]()
![]()
Problemas aplicados
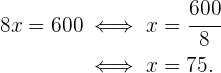
Um pai tem 35 anos e seu filho tem 5 anos. Daqui a quantos anos a idade do pai será exatamente três vezes a idade do filho? 1) A idade atual do pai é 35 anos e a do filho é 5 anos, enquanto X representa os anos que precisam passar para que a condição dada seja satisfeita. 2) Escrevemos a condição dada na forma de uma equação. 35 + x = 3(5 + x) 3) Realizamos a multiplicação. 35 + x = 3(5 + x) 35 + x = 15 + 3x 4) Subtraímos 3x e 35 em ambos os lados da equação. 35 + x - 3x - 35 = 15 + 3x - 3x - 35 -2x = -20 5) Para isolar X, multiplicamos por 6) Portanto, em 10 anos, a idade do pai será três vezes maior que a do filho. O dobro de um número menos a metade desse mesmo número é igual a 54. Qual é o número? 1) Como não conhecemos o número solicitado, representamos por X 2) Escrevemos a condição dada na forma de uma equação. 3) Multiplicamos ambos os lados da equação por 2. 4) Resolvemos a equação para encontrar X, multiplicando por 5) O número procurado é 36. A base de um retângulo é duas vezes maior que sua altura. Sabendo que o perímetro do retângulo é de 30 cm, quais são as dimensões? 1) Representamos a altura por X e, logo, sua base é 2x. 2) Escrevemos a condição do perímetro na forma de uma equação. 2(x) + 2(2x) = 30 3) Realizamos as multiplicações e somamos os termos semelhantes. 2(x) + 2(2x) = 30 2x + 4x = 30 6x = 30 4) Multiplicamos por 5) A altura é x = 5 cm e sua base é 2x = 10 cm Em uma reunião, há o dobro de mulheres em relação ao número de homens e três vezes mais crianças do que o total de homens e mulheres juntos. Quantos homens, mulheres e crianças há, considerando que são 96 pessoas no total? 1) Vamos representar o número de homens por x, mulheres como 2x (já que há o dobro delas em relação a homens) e o número de crianças como 3(x + 2x). 2) Vamos escrever em forma de equação: x + 2x + 3(x + 2x) = 96 3) Vamos fazer a multiplicação e somar os termos semelhantes: x + 2x + 3(x + 2x) = 96 x + 2x + 3x + 6x = 96 12 x = 96 4) Multiplicamos por 5) Uma vez que descobrimos que x = 8, podemos concluir que, na reunião tem 8 homens (x), 16 mulheres (2x) e 72 crianças (3(x + 2x)). Foi consumido 1) Vamos chamar a capacidade do galão de X, e como consumimos uma parte de sua capacidade, ficará 2) Ao repor 38l, a segunda condição é expressa na forma de uma equação. 3) Multiplicamos ambos os lados da equação pelo MMC (8, 5) = 40 4) Subtraímos 24x e 1520 de ambos os lados da equação. 5) E multiplicamos por 6) Assim, a capacidade do galão é de 80 litros Em uma fazenda há porcos e perus. No total, há 35 cabeças e 116 pés de animais. Quantos porcos e perus há na fazenda? 1) Chamamos de X a quantidade de cabeças de porcos, e como no total há 35 cabeças, então 35−x representa o número de cabeças de perus. 2) Escrevemos a equação referente aos pés, onde os porcos têm 4 pés e os perus têm 2. 3) Multiplicamos os valores e somamos os termos semelhantes. 4) Subtraímos 70 de ambos os lados da equação e multiplicamos ambos os lados da equação por 5) Portanto, 23 porcos e (35−23) = 12 perus. Luís fez uma viagem de carro, durante a qual consumiu 20 litros de gasolina do tanque. O trajeto foi dividido em duas etapas: na primeira, ele consumiu 1) Representamos por X os litros de gasolina que havia no tanque inicialmente.2 2) Descrevemos a condição da primeira etapa: 3) Para encontrar a quantidade de gasolina do tanque, somamos o consumo das duas etapas, que foi de 20l. 4) Resolvemos a equação: multiplicamos ambos os lados por 6 para eliminar os denominadores. Simplificamos ao multiplicar por No tanque havia 24 litros de gasolina Na primeira etapa, foram consumidos Em uma livraria, Ana compra um livro com um terço do seu dinheiro e um quadrinho com dois terços do que restava. Ao sair da livraria, ela tinha R$12. Quanto dinheiro Ana tinha inicialmente? 1) Representamos o total de dinheiro de Ana por X 2) Descrevemos a equação do valor gasto com o livro: 5) Multiplicamos ambos os lados da equação por 9 para eliminar os denominadores e somamos os termos semelhantes. 7) Multiplicamos por Assim, Ana tinha R$ 54,00 Um caminhão sai de uma cidade com uma velocidade de 40 km/h. Uma hora depois, um carro parte da mesma cidade, na mesma direção e sentido, com uma velocidade de 60 km/h. Determine o tempo necessário para que o carro alcance o caminhão. 1) Representamos o tempo percorrido pelo caminhão por t. Assim, o tempo percorrido pelo carro será t−1. 2) Ambos os veículos percorrem a mesma distância, logo podemos escrever a equação: 40t=60(t−1) 3) Expandimos a equação: 40t=60t−60 4) Subtraímos 40t de ambos os lados: 0=20t−60 5) Resolvemos para t: 20t=60 ⟹ t=3 6) Assim, o caminhão leva 3 horas para que o carro o alcance. O carro, por sua vez, leva t−1= 2 horas para alcançar o caminhão. As duas cifras de um número são consecutivas. A maior corresponde às dezenas e a menor às unidades. O número é igual a seis vezes a soma de suas cifras. Qual é o número? a) Chamamos a unidade de x. Como as cifras são consecutivas, a dezena será: x+1. b) Como temos número de duas cifras, por exemplo, 65, pode ser decomposto como: 10⋅(dezena)+(unidade) c) Nosso número será: d) Subtraímos 12 e 10 dos dois lados da equação: e) Multiplicamos por -1 nos dois lados e vamos obter Assim, O número buscado é 54. Vamos supor que você está economizando dinheiro para comprar um novo celular que custa R$700. Você tem um trabalho de meio período e ganha R$50 por dia trabalhado. Além disso, recebe uma mesada semanal de R$20 dos seus pais. Porém, gasta R$3 por cada dia que vai trabalhar. Pede-se: quantos dias por semana precisa trabalhar para comprar o celular em 8 semanas? 1) Seja x o número de dias trabalhados por semana. Assim, o valor líquido que você ganha por semana é dado por: 50x−3x+20 2) Simplificando: 47x+20 3) Agora, para 8 semanas, o total acumulado será: 8(47x+20) 4) Expandindo: 376x+160 5) Se você precisa de pelo menos $700 para comprar o celular, montamos a seguinte equação: 376x+160≥700 6) Subtraímos 160 de ambos os lados: 376x≥540 7) Dividimos ambos os lados por 376: Como 1,437 representa 2 dias inteiros trabalhados, arredondamos para cima. Assim, você precisa trabalhar pelo menos 2 dias por semana para alcançar a meta de $700 em 8 semanas. Um estudante trabalha durante o verão para economizar dinheiro para seus gastos escolares. Ele ganha $8 por hora e planeja trabalhar um número desconhecido de horas durante as férias. Seus gastos escolares somam $600. O estudante quer saber quantas horas precisa trabalhar para cobrir os gastos. Além disso, se ele só puder trabalhar 6 horas por dia, quantos dias serão necessários? Seja x o número de horas que o estudante deve trabalhar. O dinheiro ganho pode ser calculado assim: Dinheiro Ganho=(dinheiro por hora)x(horas trabalhadas) Como ele precisa de R$600, temos: O estudante precisa trabalhar 75 horas para atingir sua meta. Se ele só pode trabalhar 6 horas por dia, o número de dias necessários é: Como ele precisa completar a jornada, serão necessários 13 dias completos. Uma loja de roupas vende camisetas a um preço fixo de $15 cada uma. Além disso, a loja cobra uma taxa de envio de $5 por cada pedido realizado. Um cliente deseja comprar um número desconhecido de camisetas e está disposto a gastar no máximo $80 no total, incluindo o preço das camisetas e a taxa de envio. Quantas camisetas o cliente pode comprar sem ultrapassar seu orçamento de $80? 1) Seja x o número de camisetas que o cliente pode comprar. Então, a equação a ser considerada é: 15x+5≤80 2) Agora, isolamos a variável x: Ou seja, com um orçamento de R$80, o cliente pode comprar no máximo 5 camisetas. Uma empresa de envios oferece dois tipos de tarifas para envio de pacotes. A Tarifa A cobra R$10 de taxa fixa mais R$2 por quilo de peso do pacote. A Tarifa B cobra R$15 de taxa fixa mais R$1,50 por quilo. Qual deve ser o peso de um pacote para que ambas as tarifas sejam iguais? Seja x o peso do pacote em quilos. A condição de igualdade entre as tarifas é: Agora, isolamos o peso: Para que ambas as tarifas sejam iguais, o pacote deve pesar 10 quilos. Um cliente está comparando dois planos de telefonia celular. O Plano A tem um custo fixo mensal de R$30 mais R$0,10 por minuto de chamadas. O Plano B tem um custo fixo mensal de R$45 mais R$0,05 por minuto. Quantos minutos o cliente deve usar para que ambos os planos tenham o mesmo custo? 1) Seja x o número de minutos utilizados. A condição de igualdade entre os custos dos planos é: 3) Agora, vamos isolar o tempo em minutos - Ambos os planos custarão o mesmo quando o cliente utilizar 300 minutos.![]() ambos os lados da equação e simplificamos.
ambos os lados da equação e simplificamos.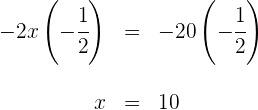
![]()
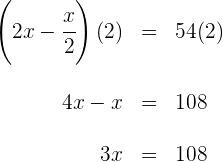
![]() .
.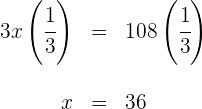
![]() os dois lados da equação:
os dois lados da equação: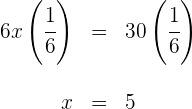
![]() os dois lados da equação
os dois lados da equação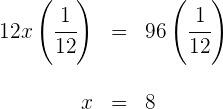
![]() de um galão de óleo. Após reabastecer 38 litros, ele ficou preenchido até
de um galão de óleo. Após reabastecer 38 litros, ele ficou preenchido até ![]() de sua capacidade. Qual é a capacidade total do galão?
de sua capacidade. Qual é a capacidade total do galão?![]()
![]()
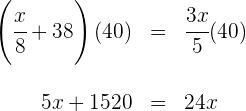
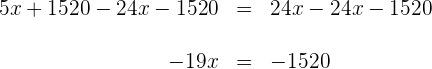
![]() nos dois lados:
nos dois lados: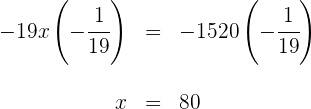
![]()
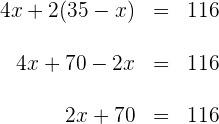
![]()
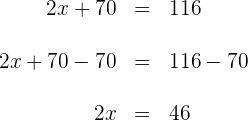
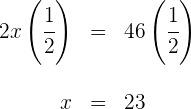
![]() da gasolina que havia no tanque, e na segunda, consumiu metade da gasolina restante. O que se pede: determinar a quantidade de litros de gasolina que havia no tanque e o consumo em cada etapa.
da gasolina que havia no tanque, e na segunda, consumiu metade da gasolina restante. O que se pede: determinar a quantidade de litros de gasolina que havia no tanque e o consumo em cada etapa.![]()
![]()

![]() e e determinamos o valor de x.
e e determinamos o valor de x.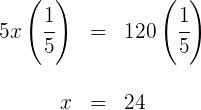
![]() , e na segunda etapa,
, e na segunda etapa, ![]() .
.![]()
3) Descrevemos a equação do valor gasto com o quadrinho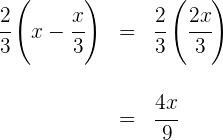
4) Para encontrar o total inicial, somamos os gastos com o livro e o quadrinho ao valor restante de R$12![]()
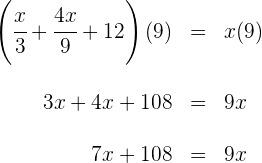
6) Subtraímos os valores adequados de ambos os lados da equação. 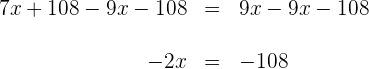
![]() para simplificar e resolver o valor de x.
para simplificar e resolver o valor de x.
![]()
![]() , vamos ter a seguinte equação:
, vamos ter a seguinte equação: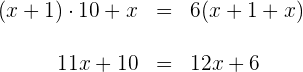
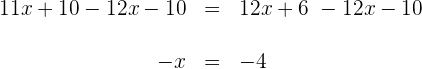
![]()
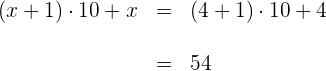



![]()
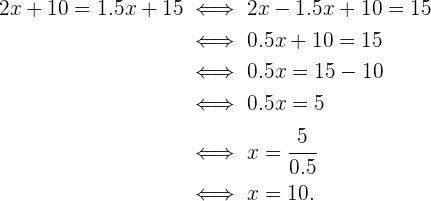
![]()
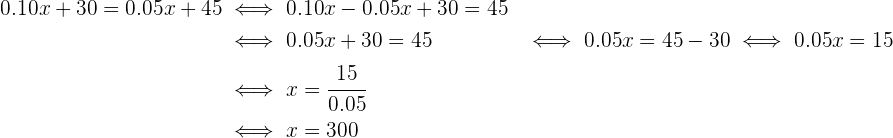
Resumir com IA:












