Temas
- Encontre a equação do segundo grau
- Fatoração
- Encontre o valor de k
- Encontre os valores solicitados
- Exercício para calcular idades
- Cálculo de um terreno
- Triângulos proporcionais
- Calcule a área do jardim
- Critério de semelhança em retângulos
- Calcule o número indicado
- Monte a equação do segundo grau e calcule
- Calcule o tempo de enchimento de uma piscina
- Encontre os valores indicados
- Cálculo de volume
- Enchendo um depósito
Bem-vindos à nossa seção dedicada à resolução de Problemas de Equações do Segundo Grau. As equações do segundo grau representam um componente essencial da matemática e sua compreensão e domínio são fundamentais para enfrentar desafios matemáticos mais complexos. Neste guia, forneceremos uma orientação passo a passo sobre a resolução de equações do segundo grau.
O processo de resolver uma equação do segundo grau começa ao igualar uma expressão polinomial de segundo grau a zero, seguido da aplicação de métodos como a fatoração, a fórmula de Bhaskara (quadrática) ou o método de completar o quadrado para determinar as soluções. À medida que avançamos nesse processo, vamos revelando as soluções matemáticas presentes em diferentes situações-problema.

Encontre a equação do segundo grau
Escreva uma equação de segundo grau cujas soluções sejam: 3 y −2.
1 Como conhecemos as raízes da equação, podemos escrevê-la da seguinte forma:
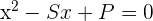
Sendo  a soma das raízes e
a soma das raízes e  o produto das raízes.
o produto das raízes.
2 Calculamos  e
e  :
:

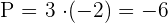
3 Assim, a equação do segundo grau procurada é

Escrever uma equação do segundo grau cujas soluções são: 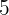 e
e 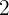
1 Agora, como ambas as raízes são positivas, consideramos a equação:
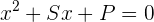
sendo  a soma das raízes e
a soma das raízes e  o produto das raízes.
o produto das raízes.
2Calculamos 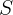 e
e 
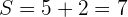
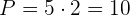
3 A equação de segundo grau procurada é:

Fatoração
Fatorize 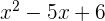
1 Resolvemos utilizando a fórmula para encontrar as raízes da equação do segundo grau:
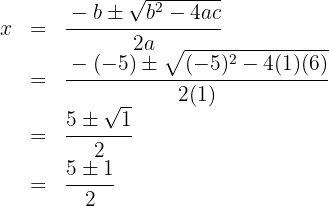
As raízes são

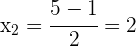
2 Conhecendo as raízes da equação, podemos fatorá-la da seguinte forma:
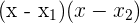
3 Assim, a fatoração procurada é
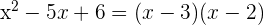
Fatorize 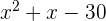
1 Resolvemos o exercício, utilizando a fórmula para encontrar as raízes da equação do segundo grau:
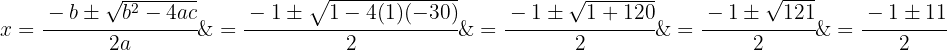
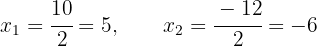
2 Conhecendo as raízes da equação, podemos fatorá-la da seguinte forma:
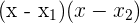
3 Assim, a fatoração procurada é:
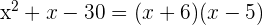
Encontre o valor de k
Determine  de modo que na equação
de modo que na equação 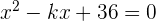 as raízes sejam iguais.
as raízes sejam iguais.
1 Para que as duas raízes sejam iguais, o discriminante  deve ser igual a zero. Calculamos o discriminante:
deve ser igual a zero. Calculamos o discriminante:
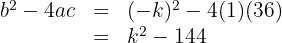
2 Igualamos o resultado a zero:
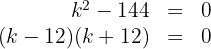
3 Igualamos cada fator a zero e determinamos os valores de  que fazem com que as raízes sejam iguais:
que fazem com que as raízes sejam iguais:
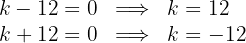
Determine  de modo que, na equação
de modo que, na equação  , as raízes sejam iguais.
, as raízes sejam iguais.
1 Para que as duas raízes sejam iguais, o discriminante 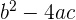 deve ser igual a zero. Calculamos o discriminante:
deve ser igual a zero. Calculamos o discriminante:
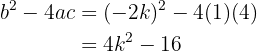
2 Igualamos o resultado a zero:
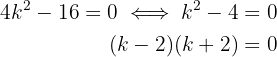
3 Igualamos cada fator a zero e determinamos os valores de  que fazem com que as raízes sejam iguais:
que fazem com que as raízes sejam iguais:
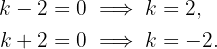
Encontre os valores solicitados
A soma de dois números é 5 e o seu produto é −84. Determine esses números.
1 Se conhecêssemos as raízes da equação, poderíamos escrevê-la da seguinte forma:
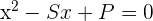
sendo  a soma das raízes e
a soma das raízes e  o produto das raízes.
o produto das raízes.
2 Sabemos que 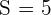 e
e 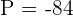 . Assim, obtemos:
. Assim, obtemos:
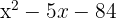
3 Resolvemos a equação do segundo grau 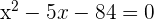 :
:

As raízes são:
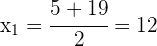
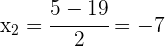
Assim, os números procurados são  e
e  .
.
A soma de dois números é −4 e o seu produto é −21. Determine esses números.
1 Se conhecêssemos as raízes da equação, poderíamos escrevê-la da seguinte forma:
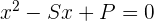
Sendo 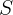 a soma das raízes e
a soma das raízes e  o produto das raízes.
o produto das raízes.
2 Sabemos que 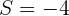 e
e 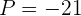 . Assim, obtemos:
. Assim, obtemos:
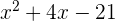
3 Resolvemos a equação do segundo grau: 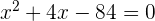
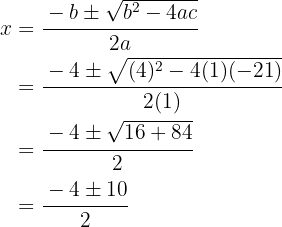
As raízes são:
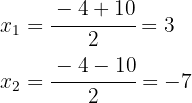
Assim, os números procurados são  e
e 
Exercício para calcular idades
Daqui a 11 anos, a idade de Pedro será a metade do quadrado da idade que ele tinha há 13 anos. Calcule a idade de Pedro.
1 Definimos as variáveis do problema:
Idade atual: 
Idade há 13 anos: 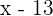
Idade daqui a 11 anos: 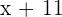
2 Montamos a equação correspondente:
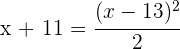
3 Elevamos o binômio ao quadrado, eliminamos o denominador e obtemos a equação:
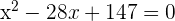
4 Resolvemos a equação:
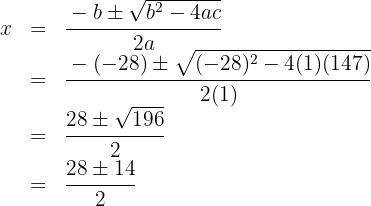
As raízes são
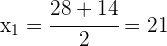

 não é uma solução válida, pois nesse caso a idade dele há 13 anos seria negativa.
não é uma solução válida, pois nesse caso a idade dele há 13 anos seria negativa.
Assim, a idade atual é  anos.
anos.
Daqui a 9 anos, a idade de Ana será igual a um quarto do quadrado da idade que ela tinha há 15 anos. Qual é a idade atual de Ana?
1 Definimos as variáveis do problema:
Idade atual: 
Idade há 15 anos: 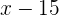
Idade daqui a 9 anos: 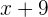
2 Montamos a equação correspondente:
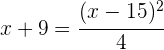
3 Elevamos o binômio ao quadrado, eliminamos o denominador e obtemos a equação:
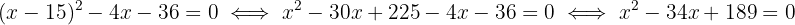
4 Resolvemos a equação:
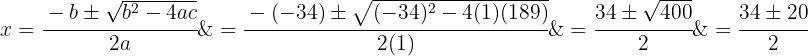
As raízes são

A idade 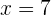 não faz sentido nesse contexto, já que estamos falando de uma pessoa que existia há pelo menos 15 anos.
não faz sentido nesse contexto, já que estamos falando de uma pessoa que existia há pelo menos 15 anos.
Portanto, Ana tem  anos.
anos.
Cálculo de um terreno
Para cercar um terreno retangular de  , foram utilizados
, foram utilizados 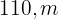 de cerca. Calcule as dimensões do terreno.
de cerca. Calcule as dimensões do terreno.
1 Representamos o terreno,

onde:
Semiperímetro: 
Base: 
Altura: 
2 A área é igual à base multiplicada pela altura:
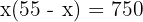
3 Eliminamos os parênteses e determinamos as raízes:
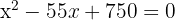
 e
e 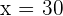
Assim, as dimensões do terreno são:
base 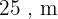 e altura
e altura 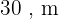
base 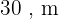 e altura
e altura 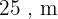
Para cercar um terreno retangular de 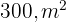 , foram utilizados
, foram utilizados 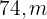 de cerca. Calcule as dimensões do terreno.
de cerca. Calcule as dimensões do terreno.
1 Representamos o terreno,
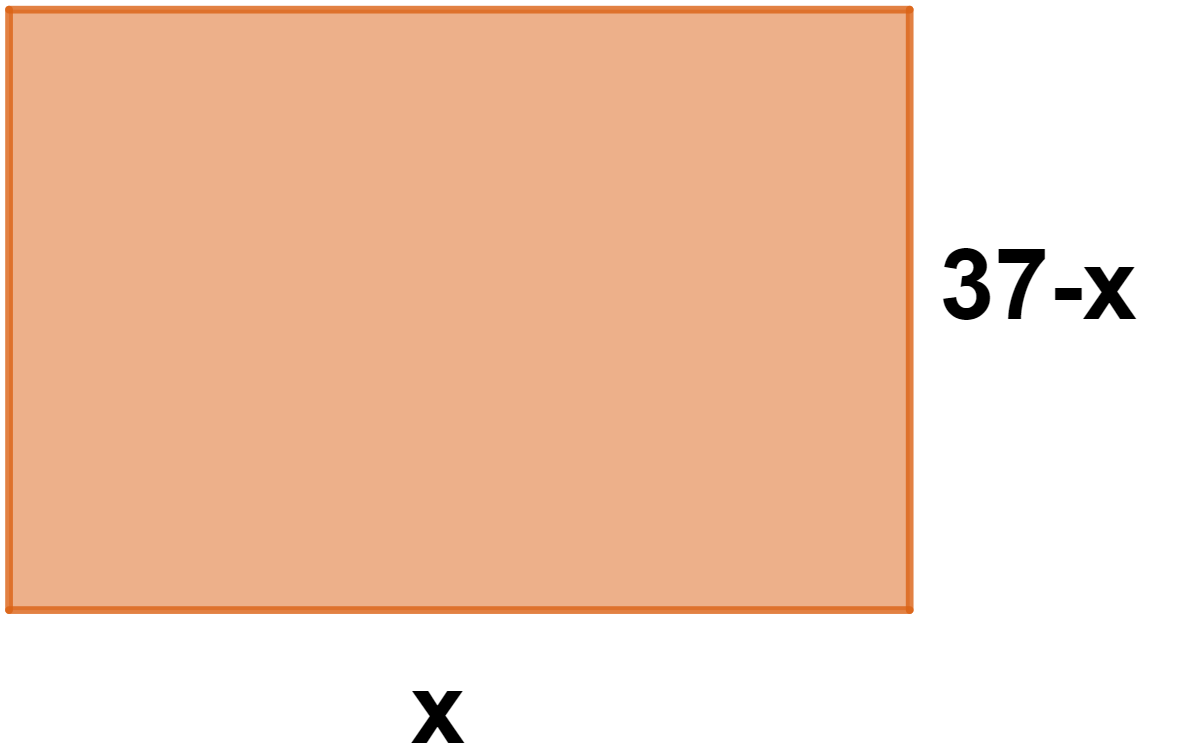
onde:
Semiperímetro: 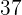
Base: 
Altura: 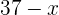
2 A área é igual à base multiplicada pela altura:
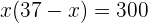
3 Desenvolvemos o produto e obtemos a equação:
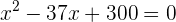
Em seguida, utilizamos a fórmula do segundo grau para encontrar as raízes:
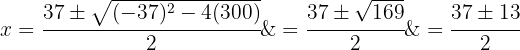
Assim, as raízes são

Portanto, as dimensões do terreno são:
base 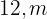 e altura
e altura 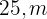 , ou, de forma equivalente,
, ou, de forma equivalente,
base 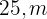 e altura
e altura 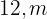 .
.
Triângulos proporcionais
Os três lados de um triângulo retângulo são proporcionais aos números 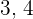 e
e  . Determine o comprimento de cada lado, sabendo que a área do triângulo é
. Determine o comprimento de cada lado, sabendo que a área do triângulo é  .
.
1 Representamos os dados fornecidos:
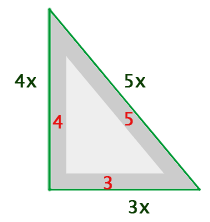
Primeiro lado:  (base)
(base)
Segundo lado:  (altura)
(altura)
Terceiro lado: 
2 Aplicamos a fórmula da área de um triângulo:

3 Eliminamos o denominador e resolvemos a equação:

 não é solução, pois um lado não pode ter comprimento negativo. Assim, as soluções são:
não é solução, pois um lado não pode ter comprimento negativo. Assim, as soluções são:
Primeiro lado: 
Segundo lado: 
Terceiro lado: 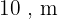
Dois lados de um triângulo isósceles são proporcionais a 10, e o lado restante é proporcional a 12. Determine o comprimento de cada lado, sabendo que a área do triângulo é  .
.
1 Representamos os dados fornecidos:
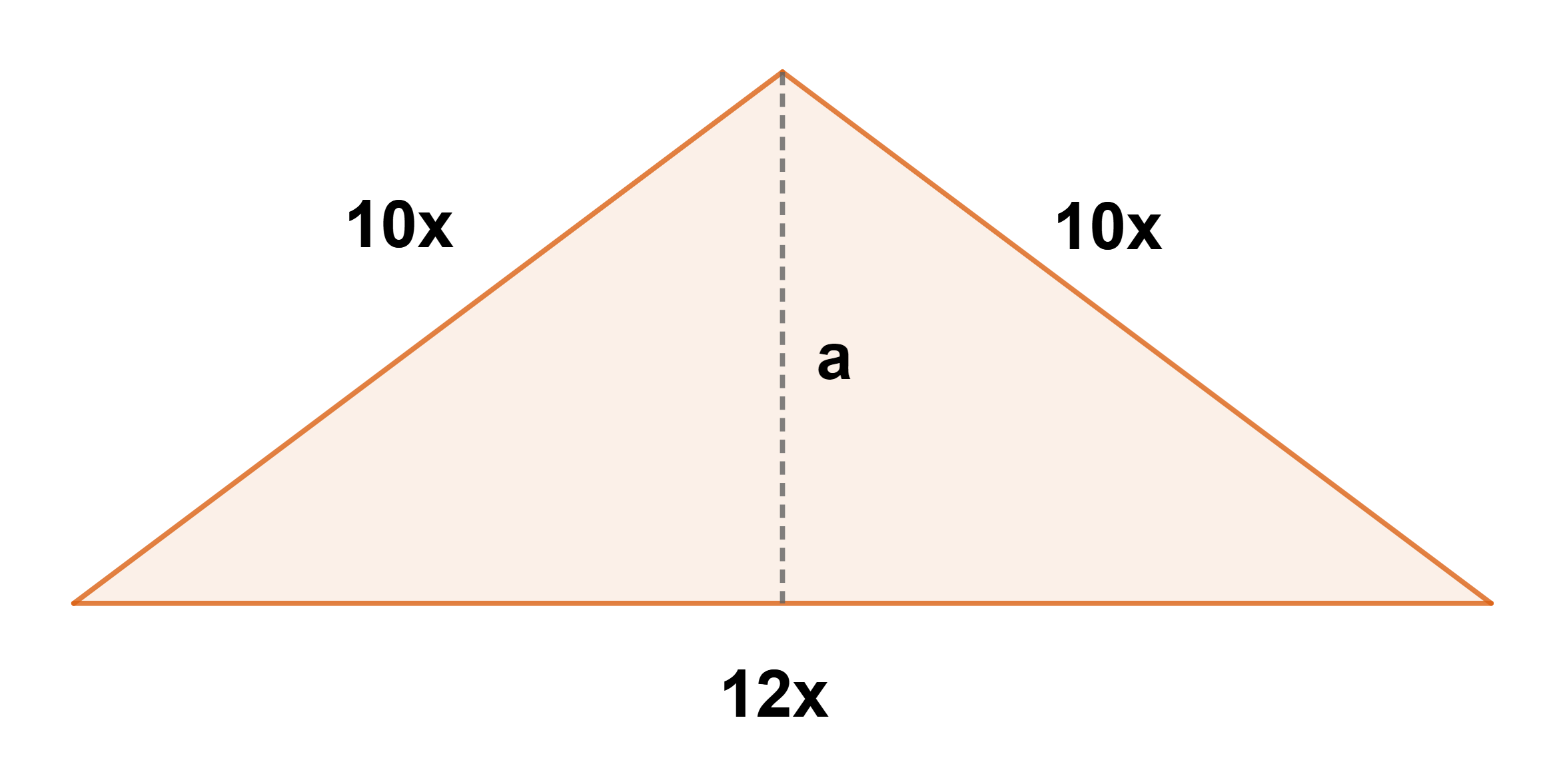
Lados iguais: 
Lado diferente:  (base)
(base)
Para obter uma expressão da área do triângulo em função de  , primeiro precisamos encontrar a altura
, primeiro precisamos encontrar a altura  . Pelo Teorema de Pitágoras,
. Pelo Teorema de Pitágoras,
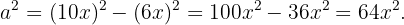
Portanto, 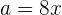
2 Aplicamos a fórmula da área de um triângulo:
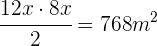
3 Isolamos  :
:
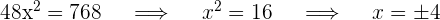
Como não podemos ter lados com comprimento negativo, a solução válida é 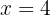 . Assim, o triângulo tem base
. Assim, o triângulo tem base 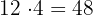 e lados iguais
e lados iguais  .
.
Calcule a área do jardim
Um jardim retangular de  de comprimento por
de comprimento por 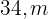 de largura é rodeado por um caminho de areia uniforme. Determine a largura desse caminho, sabendo que sua área é
de largura é rodeado por um caminho de areia uniforme. Determine a largura desse caminho, sabendo que sua área é 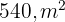 .
.
1 Representamos os dados fornecidos:

Vamos chamar de  a largura da calçada.
a largura da calçada.
2 A área da calçada é igual à área total do conjunto menos a área do jardim:
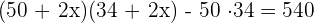
3 Eliminamos os parênteses, efetuamos as operações e simplificamos a equação dividindo ambos os membros por 4:
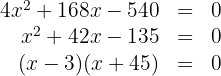
Assim, a largura da calçada é 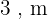 .
.
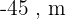 não é uma solução válida, pois as distâncias devem ser positivas.
não é uma solução válida, pois as distâncias devem ser positivas.
Uma vala tem 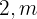 de largura e
de largura e 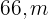 de comprimento. Se quisermos adicionar grama ao redor da vala, de modo que a área total seja de
de comprimento. Se quisermos adicionar grama ao redor da vala, de modo que a área total seja de 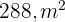 , qual deve ser a largura dessa faixa de grama?
, qual deve ser a largura dessa faixa de grama?
1 Representamos os dados fornecidos:
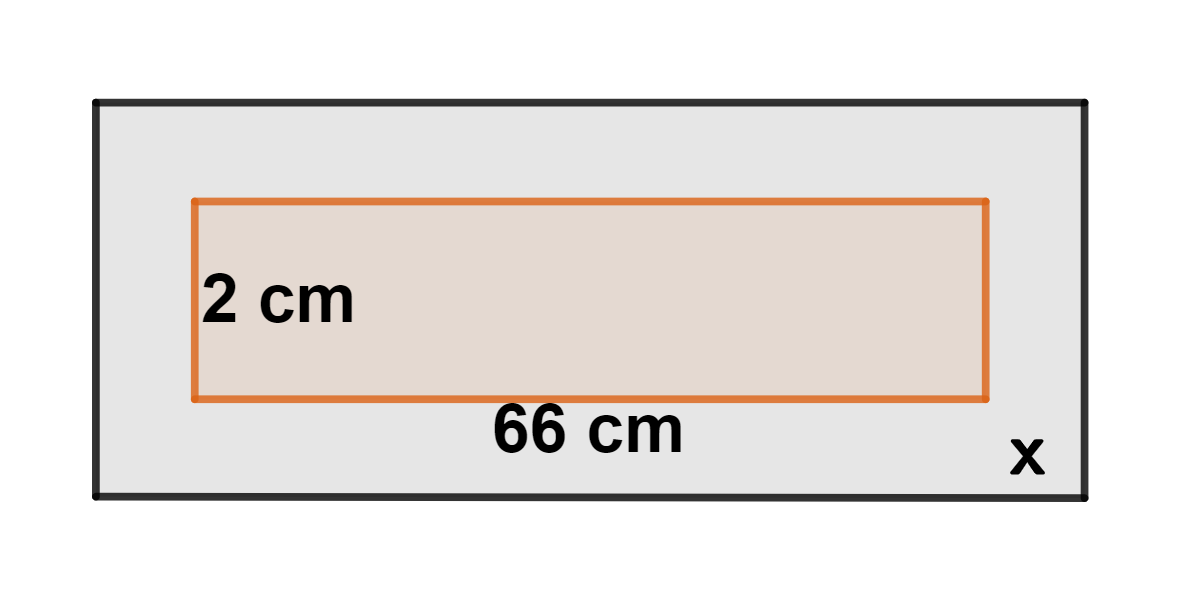
Seja  a largura da faixa de grama.
a largura da faixa de grama.
2 A área de 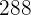 será igual à área total do conjunto sem a vala:
será igual à área total do conjunto sem a vala:
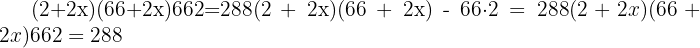
3 Desenvolvemos o produto dos polinômios e simplificamos a expressão:
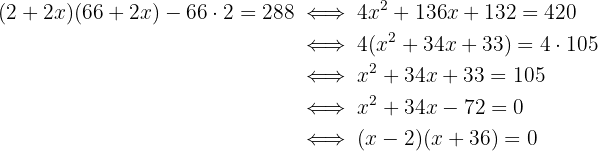
As raízes são, portanto, 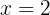 e
e 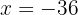 . Como estamos lidando com distâncias (valores positivos), apenas a primeira solução faz sentido. Logo, a faixa de grama deve ter largura de
. Como estamos lidando com distâncias (valores positivos), apenas a primeira solução faz sentido. Logo, a faixa de grama deve ter largura de 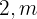 .
.
Critério de semelhança em retângulos
Calcule as dimensões de um retângulo cuja diagonal mede 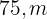 , sabendo que ele é semelhante a outro retângulo cujos lados medem
, sabendo que ele é semelhante a outro retângulo cujos lados medem  e
e 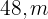 , respectivamente.
, respectivamente.
1 Os lados têm o fator comum 12, portanto, usando a semelhança, temos:
Base: 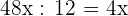
Altura: 
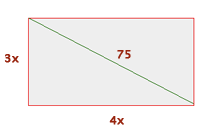
2 Aplicamos o Teorema de Pitágoras:
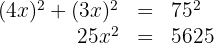
3 Resolvemos a última equação e obtemos 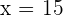 . Assim, as dimensões do retângulo pedido são:
. Assim, as dimensões do retângulo pedido são:
Base 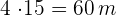
Altura 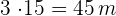
Calcule as dimensões de um retângulo cuja diagonal mede  , sabendo que ele é semelhante a outro retângulo cujos lados medem
, sabendo que ele é semelhante a outro retângulo cujos lados medem 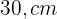 e
e 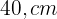 , respectivamente.
, respectivamente.
1 Os lados têm em comum o fator 5, portanto, usando a semelhança, temos:
Base: 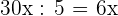
Altura: 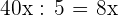
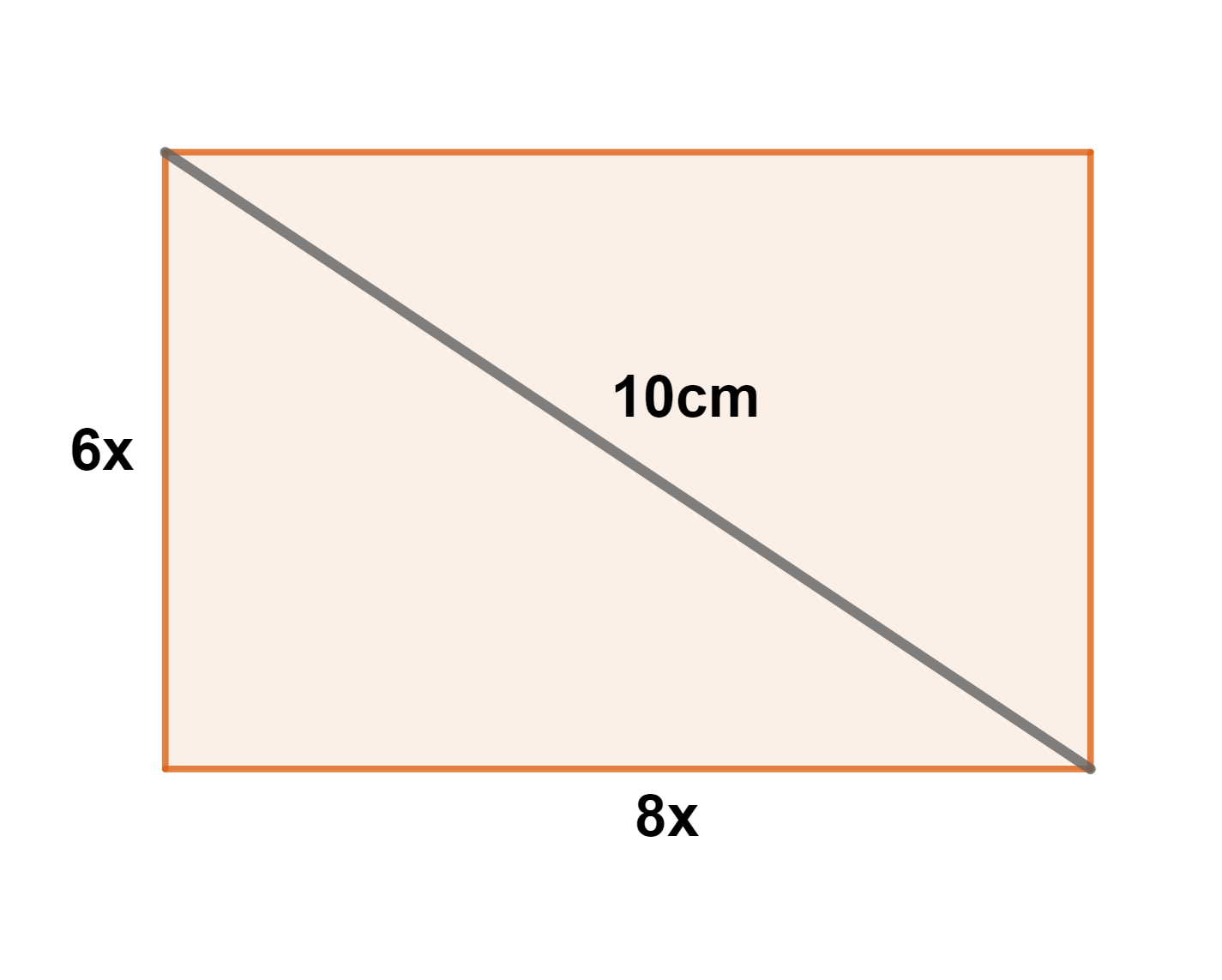
2 Aplicamos o Teorema de Pitágoras
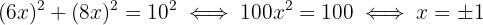
Como estamos lidando com medidas de comprimento, consideramos apenas o valor positivo. Assim, a base mede 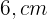 e a altura mede
e a altura mede 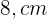 .
.
Calcule o número indicado
Determine um número inteiro sabendo que a soma dele com o seu inverso é  .
.
1 Consideramos:
Número: 
Inverso do número: 
2 Efetuamos a soma indicada:
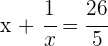
3 Resolvemos a equação racional:
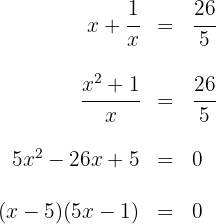
As soluções da equação são  e
e  .
.
O número pedido é  , pois
, pois  não é solução válida, já que não é um número inteiro.
não é solução válida, já que não é um número inteiro.
Determine um número inteiro sabendo que a soma dele com o seu inverso é 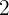 .
.
1 Consideramos:
Número: 
Inverso do número: 
2 Realizamos a soma indicada:
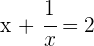
3 Resolvemos a equação racional:
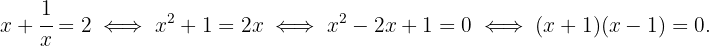
As soluções da equação são 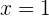 e
e 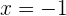 . No entanto, substituir
. No entanto, substituir 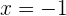 na expressão inicial não expressa o que precisamos. Portanto, a resposta é
na expressão inicial não expressa o que precisamos. Portanto, a resposta é 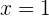 .
.
Monte a equação do segundo grau e calcule
Dois números naturais diferem em duas unidades, e a soma de seus quadrados é 580. Quais são esses números?
1 Consideramos:
Primeiro número: 
Segundo número: 
Expressamos a soma dos quadrados:
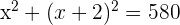
2 Elevamos o binômio ao quadrado, efetuamos as operações e simplificamos a equação dividindo ambos os membros por 2:
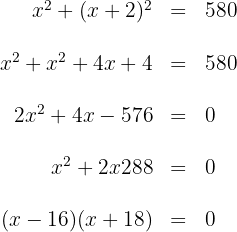
3 As soluções da equação são  e
e 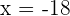
Primeiro número: 
Segundo número: 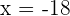
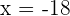 não é solução para o nosso problema, pois não é um número natural.
não é solução para o nosso problema, pois não é um número natural.
Dois números naturais diferem em cinco unidades, e a soma de seus quadrados é 277. Quais são esses números?
1 Seja  o primeiro número e
o primeiro número e  o segundo. Expressamos a soma de seus quadrados como:
o segundo. Expressamos a soma de seus quadrados como:
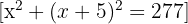
2 Elevamos o binômio ao quadrado, efetuamos as operações e simplificamos a equação:
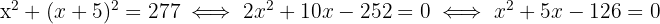
3 As soluções da equação são  e
e 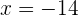 . Como
. Como 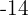 não é um número natural, tomamos
não é um número natural, tomamos  . Portanto, 9 e 14 são os números procurados.
. Portanto, 9 e 14 são os números procurados.
Calcule o tempo de enchimento de uma piscina
Dois canos  e
e 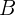 enchem juntos uma piscina em duas horas. O cano
enchem juntos uma piscina em duas horas. O cano  , sozinho, leva três horas a menos do que o cano
, sozinho, leva três horas a menos do que o cano 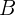 . Quantas horas cada um leva separadamente?
. Quantas horas cada um leva separadamente?
1 Consideramos:
Tempo de 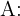

Tempo de 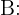

2 Em uma hora, acontece o seguinte:

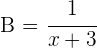
Também sabemos que, em uma hora, os dois canos juntos enchem meia piscina:

3 Substituímos:
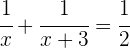
Temos uma equação racional. Para resolvê-la, primeiro precisamos eliminar os denominadores:
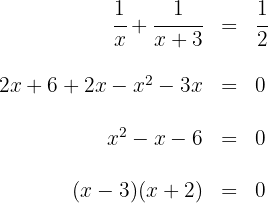
Assim, as possíveis soluções são  e
e  , mas esta última não é solução, pois o tempo seria negativo.
, mas esta última não é solução, pois o tempo seria negativo.
4 Verificamos que  é uma solução:
é uma solução:
Depois de uma hora, temos:

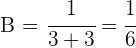
Depois de 2 horas:
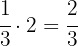
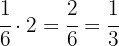
Então, em 2 horas a piscina terá sido cheia:
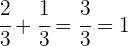
A piscina estará completamente cheia ao final de 2 horas. Assim, o tempo pedido é:
Tempo de 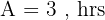
Tempo de 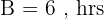
Dois canos  e
e 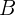 enchem juntos uma piscina em seis horas. O cano
enchem juntos uma piscina em seis horas. O cano  , sozinho, leva cinco horas a menos do que o cano
, sozinho, leva cinco horas a menos do que o cano 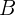 . Quantas horas cada um leva separadamente?
. Quantas horas cada um leva separadamente?
1 Seja 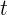 o tempo (em horas) que
o tempo (em horas) que  leva para encher a piscina. Então,
leva para encher a piscina. Então, 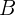 leva
leva  horas para encher a piscina. Em outras palavras, o cano
horas para encher a piscina. Em outras palavras, o cano  despeja
despeja  da capacidade total da piscina por hora. Da mesma forma, o cano
da capacidade total da piscina por hora. Da mesma forma, o cano 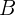 despeja
despeja  da capacidade total da piscina por hora. Também sabemos que, em uma hora, os dois canos juntos enchem um quinto da piscina:
da capacidade total da piscina por hora. Também sabemos que, em uma hora, os dois canos juntos enchem um quinto da piscina:
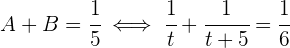
Temos uma equação racional, então vamos simplificá-la para eliminar os denominadores:
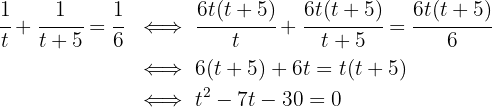
Assim, as possíveis soluções são  e
e 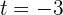 , mas esta última não é solução, pois o tempo seria negativo.
, mas esta última não é solução, pois o tempo seria negativo.
4 Verificamos que  é uma solução do problema. Isto é, deve acontecer que, em 6 horas, os canos enchem a piscina:
é uma solução do problema. Isto é, deve acontecer que, em 6 horas, os canos enchem a piscina:

Encontre os valores indicados
Os lados de um triângulo retângulo medem, em centímetros, três números pares consecutivos. Determine os valores desses lados.
1 Representamos os dados fornecidos:
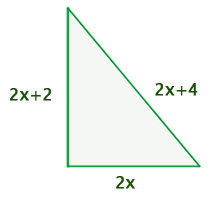
Primeiro cateto: 
Segundo cateto: 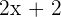
Hipotenusa: 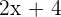
2 Aplicamos o Teorema de Pitágoras:
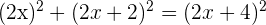
3 Elevamos os binômios ao quadrado, efetuamos as operações e simplificamos a equação, dividindo ambos os membros por 4:
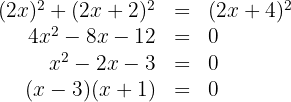
4 As soluções da equação são  e
e  . Assim, as medidas solicitadas correspondem a
. Assim, as medidas solicitadas correspondem a  :
:
Primeiro cateto: 
Segundo cateto: 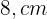
Hipotenusa: 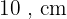
Não consideramos  , pois as distâncias devem ser positivas.
, pois as distâncias devem ser positivas.
Os lados de um triângulo retângulo medem, em centímetros, três números múltiplos de 5 consecutivos (por exemplo, 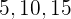 ). Determine os valores desses lados.
). Determine os valores desses lados.
1 Representamos os dados fornecidos:
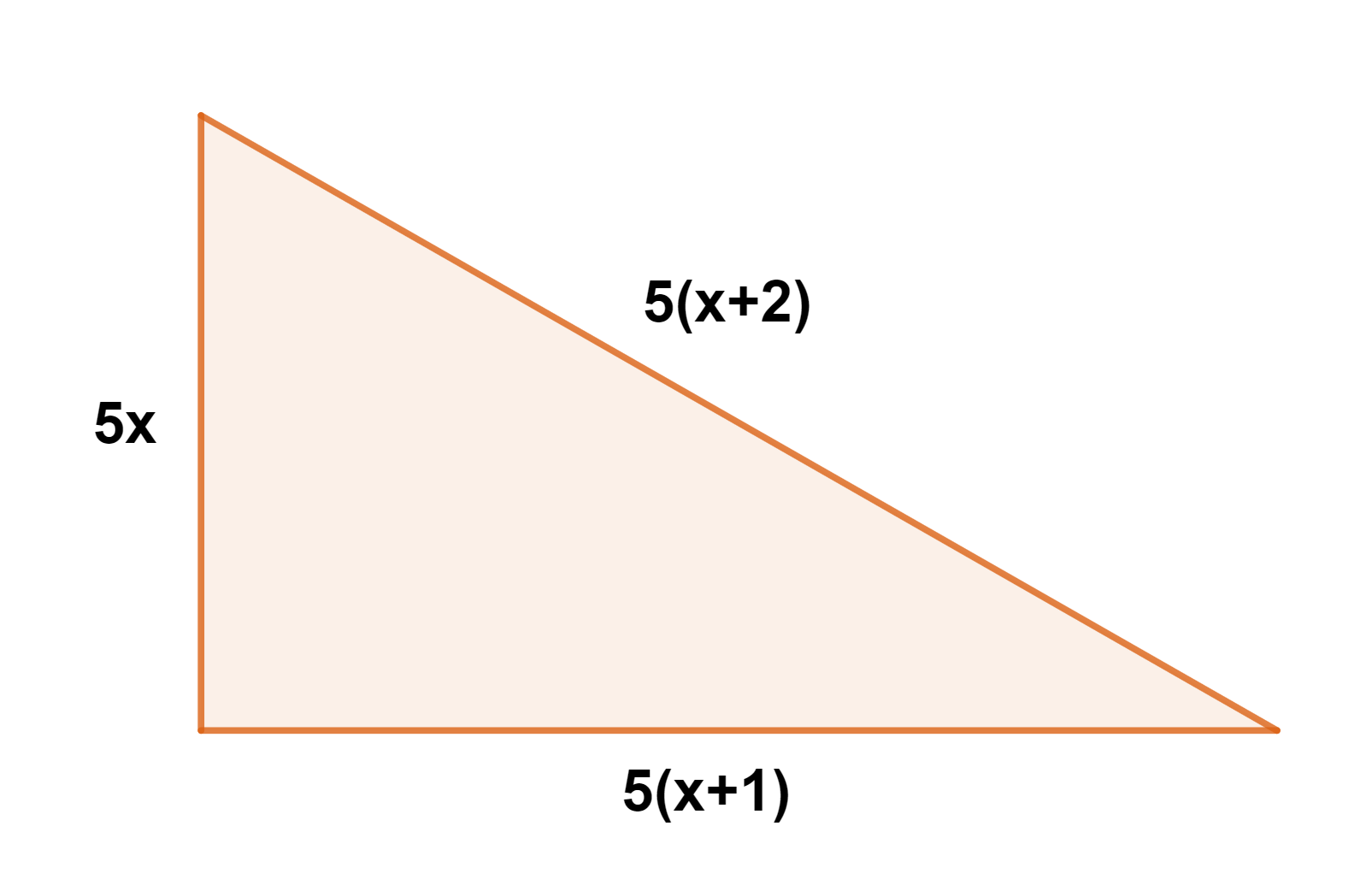
Lembramos que um múltiplo de 5 pode ser escrito como  , onde
, onde  representa um número inteiro. Assim, o triângulo tem as seguintes medidas:
representa um número inteiro. Assim, o triângulo tem as seguintes medidas:
Primeiro cateto: 
Segundo cateto: 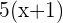
Hipotenusa: 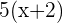
2 Aplicamos o Teorema de Pitágoras:
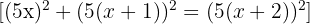
3 Elevamos os binômios ao quadrado, efetuamos as operações e simplificamos a equação dividindo tudo por 25:
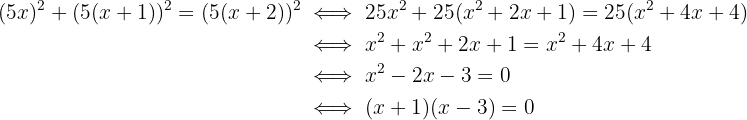
4 As soluções da equação são  e
e  . Assim, as medidas solicitadas correspondem a
. Assim, as medidas solicitadas correspondem a  :
:
Primeiro cateto: 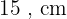
Segundo cateto: 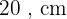
Hipotenusa: 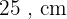
Não consideramos  , pois as distâncias devem ser positivas.
, pois as distâncias devem ser positivas.
Cálculo de volume
Uma peça retangular tem 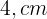 a mais de comprimento do que de largura. Com ela, constrói-se uma caixa de
a mais de comprimento do que de largura. Com ela, constrói-se uma caixa de 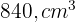 , recortando-se um quadrado de
, recortando-se um quadrado de 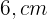 de lado em cada canto e dobrando as bordas. Determine as dimensões da caixa.
de lado em cada canto e dobrando as bordas. Determine as dimensões da caixa.
1 Representamos os dados fornecidos:
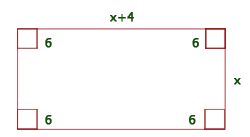
Largura: 
Comprimento: 
Altura: 
2 O volume da caixa, que é um prisma retangular, é: 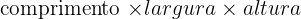
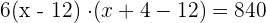 (x − 12) · (x −8) = 140
(x − 12) · (x −8) = 140
3 Resolvemos a equação anterior:

As soluções da equação são  e
e  . Assim, as medidas solicitadas são:
. Assim, as medidas solicitadas são:
Largura: 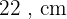
Comprimento: 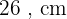
Rejeitamos a solução  , pois um comprimento não pode ser negativo.
, pois um comprimento não pode ser negativo.
Uma peça retangular tem 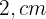 a menos de comprimento do que de largura. Com ela, constrói-se uma caixa de
a menos de comprimento do que de largura. Com ela, constrói-se uma caixa de 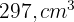 , recortando-se um quadrado de
, recortando-se um quadrado de 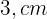 de lado em cada canto e dobrando as bordas. Determine as dimensões da caixa.
de lado em cada canto e dobrando as bordas. Determine as dimensões da caixa.
1 Representamos os dados fornecidos:
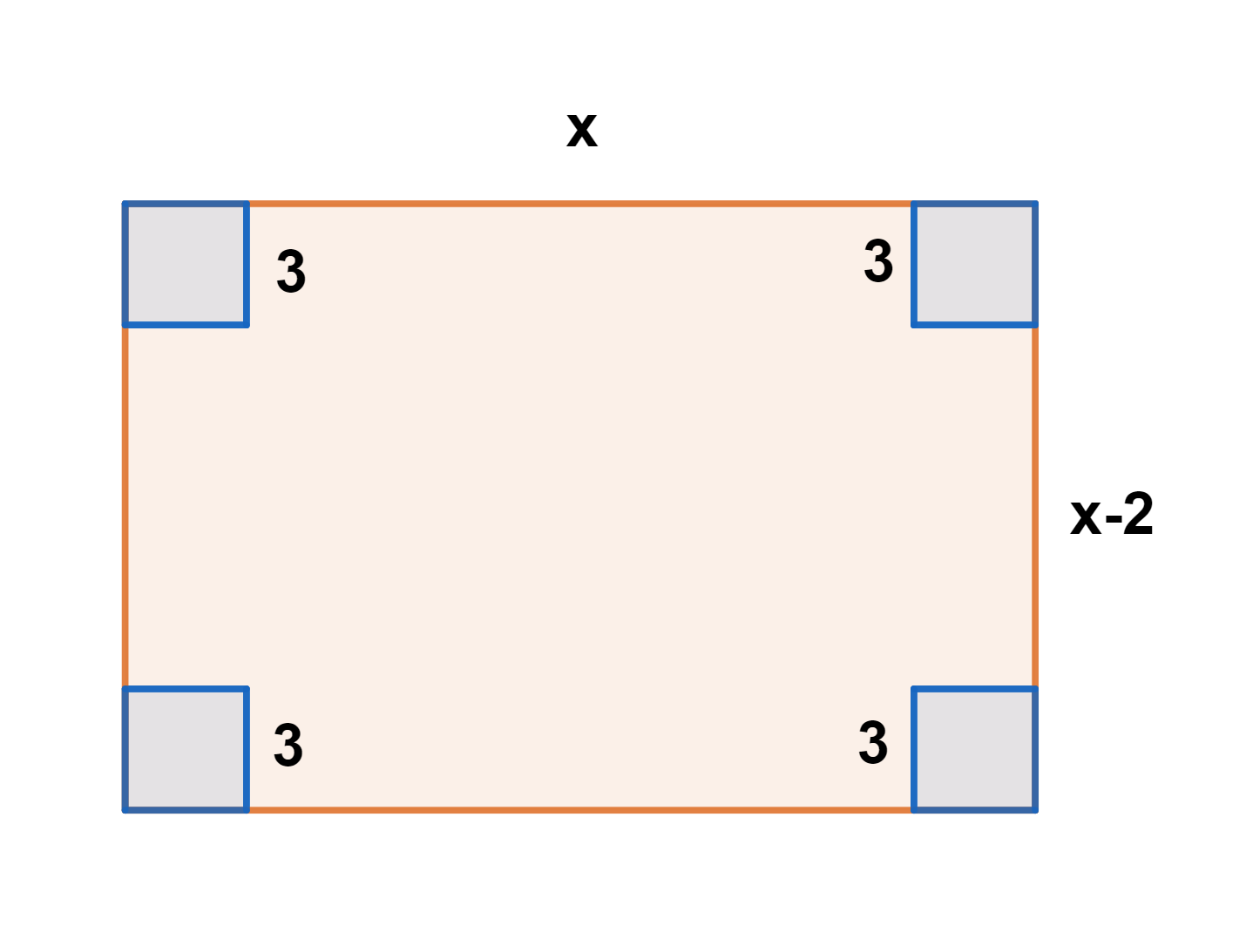
Largura: 
Comprimento: 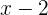
Altura: 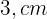
2 O volume da caixa, que é um prisma retangular, é: 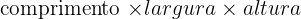
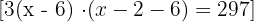
3 Resolvemos a equação anterior:
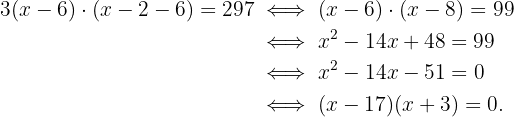
As soluções da equação são  e
e 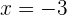 . Assim, as medidas solicitadas são:
. Assim, as medidas solicitadas são:
Largura: 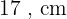
Comprimento: 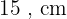
Rejeitamos a solução  , pois um comprimento não pode ser negativo.
, pois um comprimento não pode ser negativo.
Enchendo um depósito
Um cano leva duas horas a mais do que o outro para encher um reservatório. Ao abrir os dois juntos, o reservatório é preenchido em 1 hora e 20 minutos. Quanto tempo cada um leva para enchê-lo separadamente?
1 Consideramos:
Tempo do primeiro: 
Tempo do segundo: 
2 Em uma hora, acontece o seguinte:
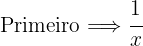
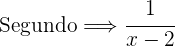
Também sabemos que em uma hora e 20 minutos, isto é, em  de hora, os dois canos juntos enchem um reservatório.
de hora, os dois canos juntos enchem um reservatório.
3 Substituímos:
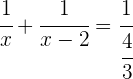
Temos uma equação racional. Para resolvê-la, primeiro precisamos eliminar os denominadores:
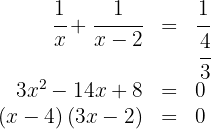
Assim, as possíveis soluções são  e
e  , mas esta última não é solução, pois o tempo gasto pelo segundo cano seria negativo.
, mas esta última não é solução, pois o tempo gasto pelo segundo cano seria negativo.
4 Assim, os tempos gastos são:
Tempo do primeiro: 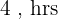
Tempo do segundo: 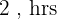
Um cano leva cinco horas a mais do que o outro para encher um reservatório. Ao abrir os dois juntos, o reservatório é preenchido em 3 horas e 20 minutos. Quanto tempo cada um leva para enchê-lo separadamente?
1 Seja 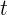 o tempo que o primeiro cano leva para encher o reservatório. Então, o segundo leva
o tempo que o primeiro cano leva para encher o reservatório. Então, o segundo leva 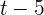 . Em uma hora, o primeiro cano enche
. Em uma hora, o primeiro cano enche  da capacidade total do reservatório, enquanto o segundo enche
da capacidade total do reservatório, enquanto o segundo enche  .
.
Também sabemos que em três horas e 20 minutos, isto é,  de hora, os dois canos juntos enchem completamente o reservatório.
de hora, os dois canos juntos enchem completamente o reservatório.
3 Substituímos:
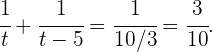
Temos uma equação racional. Para resolvê-la, primeiro precisamos eliminar os denominadores:
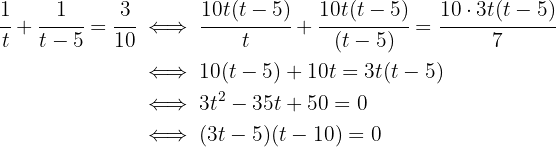
Assim, as possíveis soluções são  e
e  , mas esta última não é solução, pois o tempo gasto pelo segundo cano seria negativo.
, mas esta última não é solução, pois o tempo gasto pelo segundo cano seria negativo.
4 Portanto, os tempos gastos são:
Tempo do primeiro: 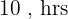
Tempo do segundo: 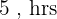
Resumir com IA:












