O cálculo da área de polígonos é uma habilidade fundamental da geometria, com aplicações em diversas áreas, como arquitetura, design, topografia e muitas outras disciplinas práticas.
Compreender como determinar essas áreas não apenas reforça os conceitos geométricos básicos, mas também desenvolve habilidades analíticas e de raciocínio lógico.
Neste material, você encontrará uma série de exercícios resolvidos que abrangem diferentes tipos de polígonos, como triângulos, quadriláteros, pentágonos e figuras mais complexas.
Cada exercício foi elaborado para ajudar você a aplicar fórmulas específicas, interpretar dados e resolver problemas passo a passo
Um campo retangular tem base de  m e altura de
m e altura de  m. Calcule:
m. Calcule:
A O número de hectares do campo.
B O preço do campo, sabendo que o metro quadrado custa R$  .
.
A Calculamos a área do retângulo multiplicando a base pela altura:
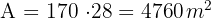
Sabemos que 1 hectare = 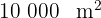 , portanto, o número de hectares do campo é:
, portanto, o número de hectares do campo é:
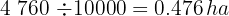
BPara calcular o preço do campo, se cada metro quadrado custa R$  , fazemos:
, fazemos:
R$ 
Um campo de beisebol tem um “diamante” (nome usado em inglês para o formato quadrado do campo) com lado de de 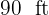 de lado. Calcule sua área.
de lado. Calcule sua área.
O “diamante” de um estádio de beisebol é, na verdade, um quadrado, portanto, a área procurada é:
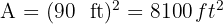
Uma quadra de basquete mede 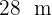 de comprimento por
de comprimento por 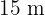 de largura. Se o custo de manutenção é de R$ 12 por metro quadrado, encontre o custo total da manutenção da quadra.
de largura. Se o custo de manutenção é de R$ 12 por metro quadrado, encontre o custo total da manutenção da quadra.
A área total da quadra de basquete é:
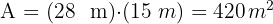
O custo total da manutenção é:
R$ 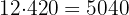
Um campo de futebol mede 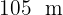 de comprimento por
de comprimento por 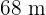 de largura e consome 55000 litros de água por dia para irrigação. Uma nova tecnologia de aspersores permite irrigar um metro quadrado com cinco litros de água. Quantos litros de água por dia serão economizados com essa nova tecnologia?
de largura e consome 55000 litros de água por dia para irrigação. Uma nova tecnologia de aspersores permite irrigar um metro quadrado com cinco litros de água. Quantos litros de água por dia serão economizados com essa nova tecnologia?
A área total do campo de futebol é:
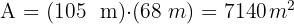
A economia total de água é:
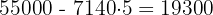 litros
litros
Um litro de tinta cobre cinco metros quadrados de superfície. Quantos litros de tinta são necessários para pintar uma parede de dez metros de comprimento por quatro de altura?
A área total da parede é:
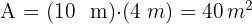
A quantidade de litros necessária é:
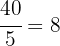 litros
litros
Determine o número de ladrilhos quadrados, com lado medindo  cm, necessários para cobrir uma área retangular de
cm, necessários para cobrir uma área retangular de  m de base por
m de base por  m de altura.
m de altura.
1 Calculamos a área do retângulo, multiplicando a base pela altura:
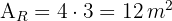
2Sabemos que 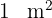 equivale a
equivale a  , logo, a área do retângulo em centímetros quadrados é:
, logo, a área do retângulo em centímetros quadrados é:
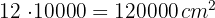
3Calculamos a área de um ladrilho:
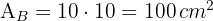
4Para calcular o número de ladrilhos necessários, dividimos a área total pelo valor da área de um ladrilho:
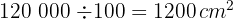
Assim, são necessários 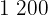 ladrilhos.
ladrilhos.
Calcule a área de um triângulo retângulo isósceles cujos lados medem  cm cada.
cm cada.
1 Desenhamos o triângulo retângulo isósceles:
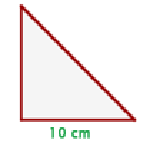
2Observamos que os lados iguais correspondem à base e à altura do triângulo.
3Calculamos a área, que é igual ao produto da base pela altura dividido por dois:
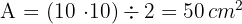
O perímetro de um triângulo equilátero mede  dm e sua altura mede
dm e sua altura mede  cm. Calcule a área do triângulo.
cm. Calcule a área do triângulo.
1 Desenhamos o triângulo equilátero.
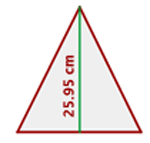
2Observamos que o perímetro está em  e a altura em
e a altura em  . Convertendo o perímetro para centímetros:
. Convertendo o perímetro para centímetros:
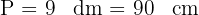
Para calcular a área do triângulo, precisamos conhecer sua base e sua altura. Como o triângulo é equilátero, seus três lados são iguais, portanto, o valor de um lado é obtido dividindo o perímetro por três:
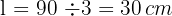
A área do triângulo é igual ao produto da base pela altura dividido por dois:

Calcule o número de árvores que podem ser plantadas em um terreno retangular de  de comprimento e
de comprimento e  e largura, sabendo que cada árvore precisa de
e largura, sabendo que cada árvore precisa de 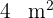 para se desenvolver.
para se desenvolver.
1 Calculamos a área do terreno retangular, que é igual ao produto de seu comprimento pela largura:
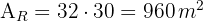
Observamos que cada árvore precisa de 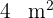 , para se desenvolver. Portanto, para calcular o número de árvores, dividimos a área total do terreno por quatro:
, para se desenvolver. Portanto, para calcular o número de árvores, dividimos a área total do terreno por quatro:
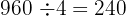
Assim, o número de árvores que podem ser plantadas é  .
.
A área de um trapézio é 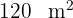 , a altura mede
, a altura mede  , e a base menor mede
, e a base menor mede  . Quanto mede a outra base?
. Quanto mede a outra base?
1 Escrevemos a fórmula da área de um trapézio, que é igual à metade do produto da altura pela soma das bases:

2Substituímos os valores conhecidos:
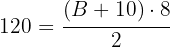
3Simplificamos o lado direito, dividindo oito por dois:

4Queremos isolar  , portanto, dividimos ambos os lados por quatro:
, portanto, dividimos ambos os lados por quatro:

5Subtraímos dez de ambos os lados e obtemos:
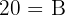
Assim, a outra base mede 
Calcule a área de um paralelogramo cuja altura mede  cm e cuja base mede
cm e cuja base mede  vezes a sua altura.
vezes a sua altura.
1 Para calcular a área, precisamos conhecer a base e a altura. A altura mede  e a base mede três vezes esse valor. Assim, a base é:
e a base mede três vezes esse valor. Assim, a base é:
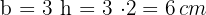
2Calculamos a área, que é igual ao produto da base pela altura:
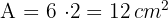
Calcule a área de um losango cuja diagonal maior mede  cm e cuja diagonal menor é a metade da maior.
cm e cuja diagonal menor é a metade da maior.
1 Para calcular a área, precisamos conhecer a diagonal maior e a diagonal menor do losango. A diagonal maior mede 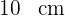 e a menor mede a metade da maior. Portanto, o valor da diagonal menor é:
e a menor mede a metade da maior. Portanto, o valor da diagonal menor é:

2Calculamos a área, que é igual à metade do produto das diagonais:

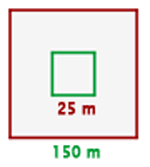
No centro de um jardim quadrado de  m de lado há uma piscina também quadrada, de
m de lado há uma piscina também quadrada, de  m de lado. Calcule a área do jardim.
m de lado. Calcule a área do jardim.
1 Representamos graficamente o problema e percebemos que a área total é igual à soma da área do jardim e da área da piscina.
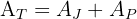
2Calculamosa área total, que é igual ao produto dos lados do quadrado.

3Calculamos a área da piscina, que também é o produto dos lados do quadrado.
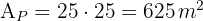
4Assim, a área do jardim é igual à área total menos a área da piscina:
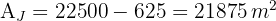
Calcule a área do quadrilátero formado ao unir os pontos médios dos lados de um retângulo cuja base e altura medem  cm e
cm e  cm.
cm.
1 Representamos graficamente o problema e notamos que a figura formada é composta por quatro triângulos retângulos de base  e altura
e altura 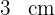
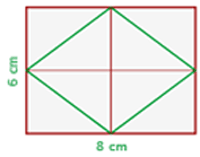
2Calculamos a área do triângulo:
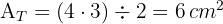
3Calculamos a área do quadrilátero:

Quanto vale a área da parte destacada da figura, se a área do hexágono é:
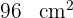 .
.
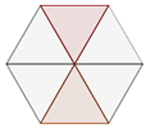
1 Observamos que o hexágono é composto por seis triângulos iguais.
2 Calculamos a área de um triângulo:

3Calculamos a área da parte destacada:
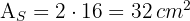
Uma área arborizada tem formato de trapézio, cujas bases medem  m e
m e  m. A altura da área é
m. A altura da área é  m. Constrói-se uma calçada de
m. Constrói-se uma calçada de  m de largura, perpendicular às duas bases.
m de largura, perpendicular às duas bases.
Calcule a área da parte que continua arborizada.
1 Representamos graficamente o problema e notamos que a área total do trapézio é igual à soma da área da parte arborizada e da área da calçada
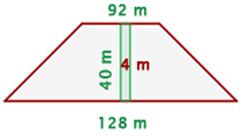
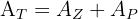
2Calculamos a área do trapézio.
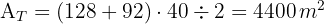
3Calculamos el área da calçada:

4Calculamos a área da parte arborizada:

Um jardim retangular mede  m por
m por  m. O jardim é cortado por duas calçadas perpendiculares que formam uma cruz. Uma delas tem
m. O jardim é cortado por duas calçadas perpendiculares que formam uma cruz. Uma delas tem  dm de largura e a outra
dm de largura e a outra  dm.
dm.
Calcule a área do jardim.
1 Representamos graficamente o problema e percebemos que a área do jardim é igual à área do retângulo menos as áreas das calçadas, mais a área da interseção entre elas:
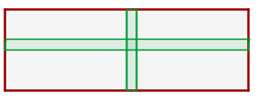

2Calculamos a área do retângulo:

3Calculamos a área da primeira calçada:
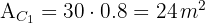
4Calculamos a área da segunda calçada:
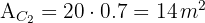
5Calculamos a área da interseção das calçadas:

6Calculamos a área do jardim:
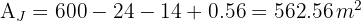
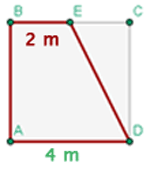
Considerando o quadrado  com lado medindo
com lado medindo 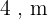 , une-se o ponto
, une-se o ponto  , que é o ponto médio do lado
, que é o ponto médio do lado  , ao vértice
, ao vértice  . Determine a área do trapézio formado.
. Determine a área do trapézio formado.
1 Representamos graficamente o problema e notamos que a área do trapézio é igual à área do quadrado menos a área de um triângulo retângulo

2Calculamos a área do quadrado:

3Calculamos a área do triângulo:
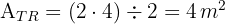
4Calculamos a área do trapézio:
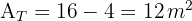
Calcule a quantidade de tinta necessária para pintar a fachada deste prédio, sabendo que é utilizado  kg de tinta por
kg de tinta por  .
.
1 Notamos que a fachada é formada por um triângulo de base  e altura
e altura 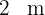 , dois retângulos de base
, dois retângulos de base  e altura
e altura 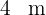 ; e dois triângulos retângulos de base
; e dois triângulos retângulos de base 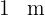 e altura
e altura 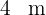 .
.

2Calculamos a área do triângulo:
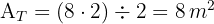
3Calculamos a área do retângulo:

4Calculamos a área do triângulo retângulo:

5Calculamos a área total da fachada:

6Calculamos a quantidade de tinta necessária:
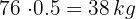
Calcule o perímetro e a área da figura:
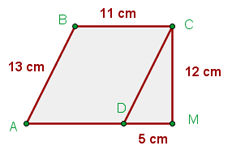
1 Notamos que a figura é composta por um paralelogramo de base  e altura
e altura 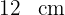 e por um triângulo retângulo de base
e por um triângulo retângulo de base  e altura
e altura 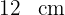 , de forma que sua área é:
, de forma que sua área é:

2Calculamos a área do triângulo:

3Calculamos a área do paralelogramo:
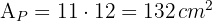
4Calculamosa área total da figura:
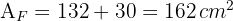
5Calculamos o perímetro:
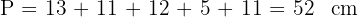
Resumir com IA:


