Temas
Para elevar uma fração a uma potência se aplica o exponente tanto o numerador como o denominador.
sempre que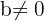 
Exemplo: Desenvolva a potência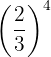 
Potências de frações com expoente negativo
Uma potência de uma fração com expoente negativo é igual a outra potência cuja base é a inversa da fração original e com expoente positivo
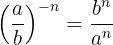
Exemplo: Desenvolva a potência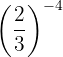 
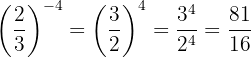
Propriedades das potências de frações
Toda fração elevada á potência zero é igual a um.
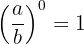
Toda fração elevada a potência um é igual a mesma fração.
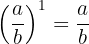
O produto de potências com a mesma base é a outra potência com a mesma base e seu expoente é igual a soma dos exponentes.
A divisão de potências com a mesma base é outra potência com a mesma base e seu expoente é igual a diferença dos exponentes.
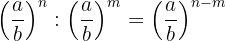
A potência de uma potência é outra potência com a mesma base e seu exponente é igual ao produto dos exponentes.
O produto de potências com o mesmo exponente é outra potência com o mesmo expoente e sua base é igual ao produto das bases.
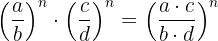
O quociente de potências com o mesmo exponente é outra potência com o mesmo expoente e sua base é igual ao quociente das bases.
Exercícios propostos
As potências tem a mesma base, então pela propriedade 3 a base é a mesma e se somam os exponentes
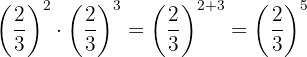
As potências têm a mesma base, portanto pela propriedade 3 a base é a mesma e se somam os exponentes
Pela propriedade 2 toda fração elevada a potência um, é igual a mesma fração
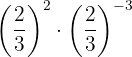
As potências têm a mesma base, enem de acordo com a propriedade 3 a base é a mesma e se somam os exponentes
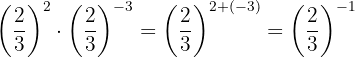
Para eliminar o sinal negativo do expoente, precisamos escrever a fração inversa e então aplicar a propriedade 2, isso nos diz que qualquer fração elevada à potência de um é igual à própria fração.
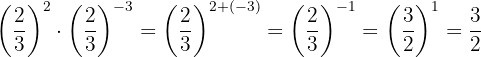
As potências têm a mesma base, então pela propriedade 3 a base é a mesma e os expoentes são somados
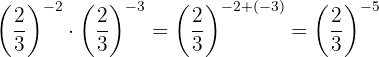
Para remover o sinal negativo do expoente, temos que escrever a fração recíproca
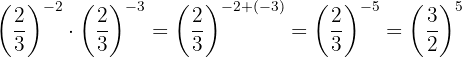
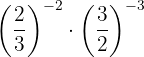
Como as potências não têm a mesma base, tomamos a fração inversa da segunda potência para obter um expoente positivo.
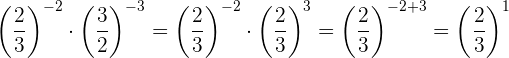
De acordo com a propriedade 2 toda fração elevada à potência de um é igual à própria fração.
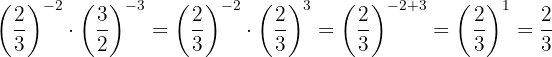
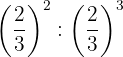
As potências têm a mesma base, então pela propriedade 4 a base é a mesma e os expoentes são subtraídos
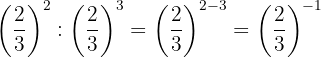
Para remover o sinal negativo do expoente, temos que escrever a fração recíproca; então pela propriedade 2 toda fração elevada à potência de um é igual à própria fração.
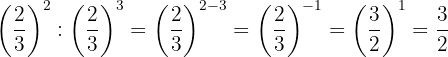
As potências têm a mesma base, então pela propriedade 4 a base é a mesma e se subtraem os exponentes
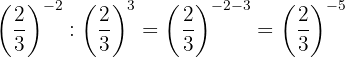
Para remover o sinal negativo do expoente, temos que escrever a fração recíproca
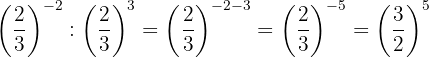
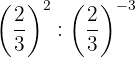
As potências têm a mesma base, então pela propriedade 4 a base é a mesma e os expoentes são subtraídos
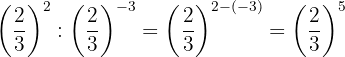
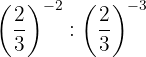
As potências têm a mesma base, então pela propriedade 4 a base é a mesma e os expoentes são subtraídos.
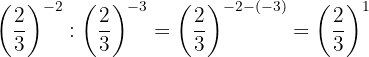
Pela propriedade 2 toda fração elevada a potência um, é igual à própria fração
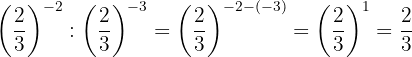
Tomamos a fração inversa da primeira potência para mudar o sinal do expoente.
As potências têm a mesma base, então pela propriedade 4 a base é a mesma e os expoentes são subtraídos.
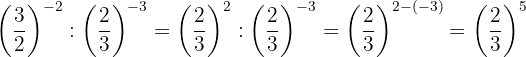
Se trata da potência de uma potência, então pela propriedade 5 a base é a mesma e os expoentes são multiplicados.
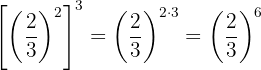
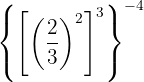
Se trata da potência de uma potência, então pela propriedade 5 a base é a mesma e os expoentes são multiplicados
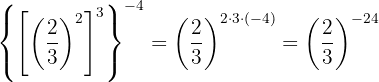
Para remover o sinal negativo do expoente, temos que escrever a fração recíproca
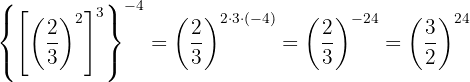
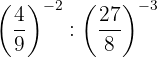
Vamos decompor os números em fatores e aplicar a propriedade 5 de potência de uma potência
Vamos usar a fração inversa da primeira potência para mudar o sinal do expoente e aplicamos a propriedade 4 de quociente de potências
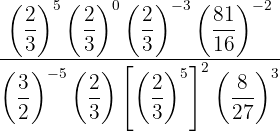
Vamos tentar colocar todas as frações com o mesmo numerador e denominador, para isso, decomponha em fatores os números que não sejam primos.
Temos elementos que são potências de potências, então vamos aplicar a propriedade 5 para escrevê-los como uma única potência.
Para as potências com base 
e expoentes negativos, vamos colocar a fração inversa com expoente positivo.
Tanto o numerador como o denominador, multiplicamos as potências pela mesma base, empregando a propriedade 3 e dividimos os resultados usando a propriedade 4. Finalmente, colocamos a fração inversa com expoente positivo.
Gostou desse artigo? Deixe uma nota!
Loading...
